O is the centre of an equilateral triangle ABC. and are three forces acting along the sides AB, BC and AC as shown in the figure. What should be the magnitude of , so that the total torque about O is
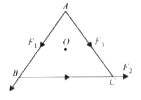
The correct Answer is:A
Let x be the distance to point O of the equilateral triangle from each side. Total torque about O.
or
Topper's Solved these Questions
- MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONBook:MTG-WBJEEChapter:MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONExercise:WB-JEE WORKOUT (CATEGORY 2 : Single Option Correct Type (2 Marks))
Explore 25 Videos
- MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONBook:MTG-WBJEEChapter:MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONExercise:WB-JEE Previous years questions
Explore 17 Videos
- MODEL TEST PAPTER Book:MTG-WBJEEChapter:MODEL TEST PAPTER Exercise:MCQs
Explore 80 Videos
- NUCLEAR PHYSICBook:MTG-WBJEEChapter:NUCLEAR PHYSICExercise:WB JEE PREVIOUS YEARS QUESTIONS
Explore 5 Videos
Similar Questions
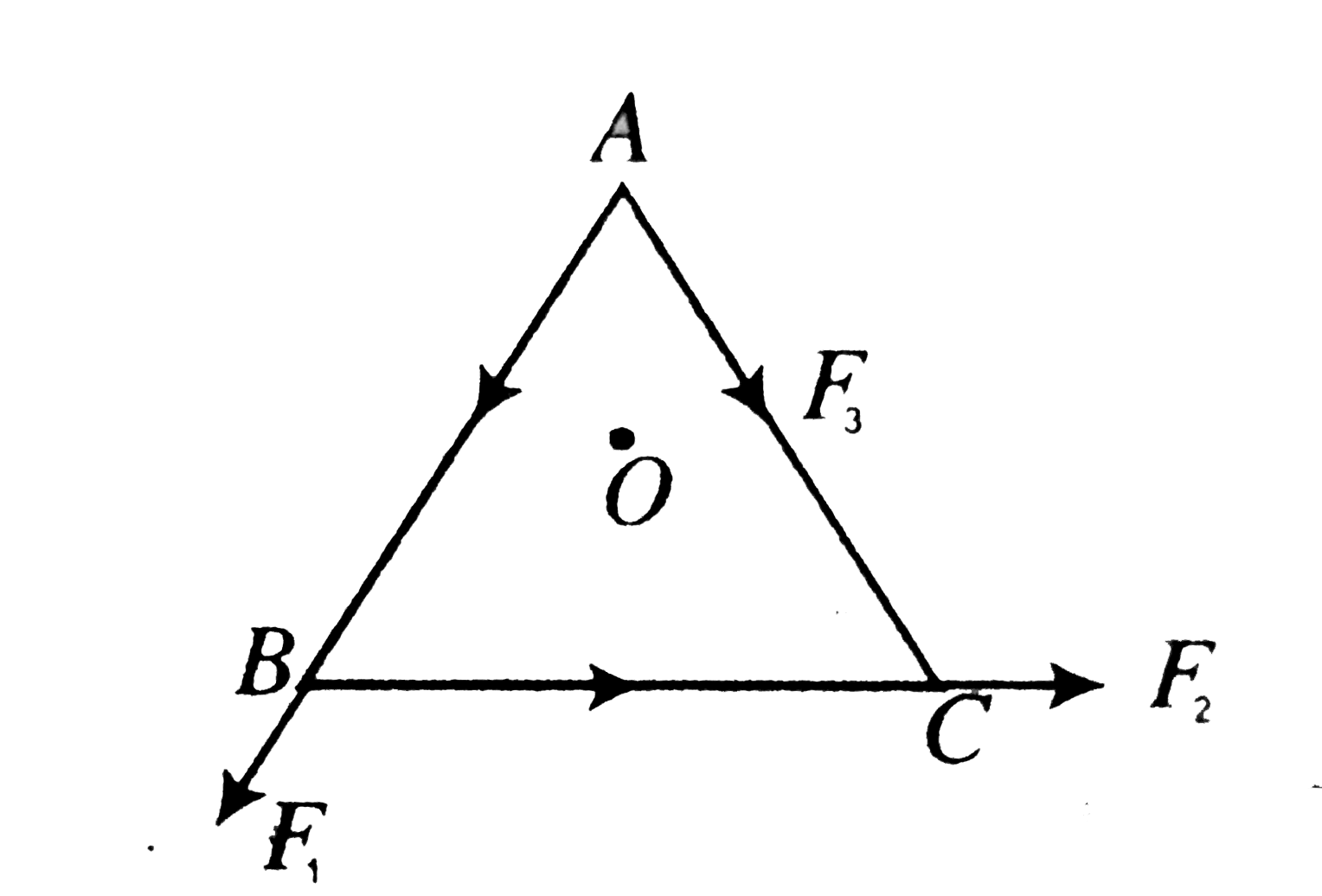
O is the centre of an equilateral triangle ABC. F1,F2 and F3 are the three forces acting along the sides AB,BC and AC respectively. What should be the value of F3 so that the total torque about O is zero?
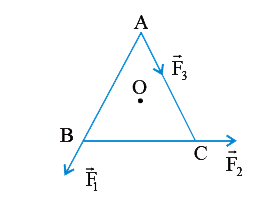
View SolutionABC is an equilateral with O as its centre →F1,→F2 and →F3 represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero then the magnitude of →F3 is :
View Solution
Knowledge Check
O is the centre of an equilateral triangle ABC. F1,F2 and F3 are the three forces acting along the sides AB,BC and AC respectively. What should be the value of F3 so that the total torque about O is zero?
 A2(F1+F2)BF1+F22CF1−F2DF1+F2
A2(F1+F2)BF1+F22CF1−F2DF1+F2Given an equilateral triangle ABC, D, E and F are the mid-points of the sides AB, BC and AC respectively, then the quadrilateral BEFD is exactly a
AsquareBrectangleCparallelogramDrhombusTwo forces F1 and F2 are acting on a rod abc as shown in figure.
 Aif F1=F2 then τa=τb=τc ( for both forces)Bif F1=F2 then τa=τc≠τb ( for both forces)Cif F1≠F2 then τa≠τb≠τc ( for both forces)Dif F1≠F2 then τa=τc≠τb ( for both forces)
Aif F1=F2 then τa=τb=τc ( for both forces)Bif F1=F2 then τa=τc≠τb ( for both forces)Cif F1≠F2 then τa≠τb≠τc ( for both forces)Dif F1≠F2 then τa=τc≠τb ( for both forces)
ABC is an equilateral triangle with O as its centre −→F1,−→F2 and −→F3 represent three forces acting along the sides AB, BC and AC respectively. If the torque about O is zero then the magnitude of −→F3 is

View SolutionTwo forces F1 and F2 are acting on a rod abc as shown in figure.

View SolutionThree forces of magnitude F, F and √2F are acting on the periphery of a disc of mass m and radius R as shown in the figure. The net torque about the centre of the disc is
View SolutionThere are four forces ,acting at a point P produced by strings as shown in figure. which is at rest. The forces F1andF2 are
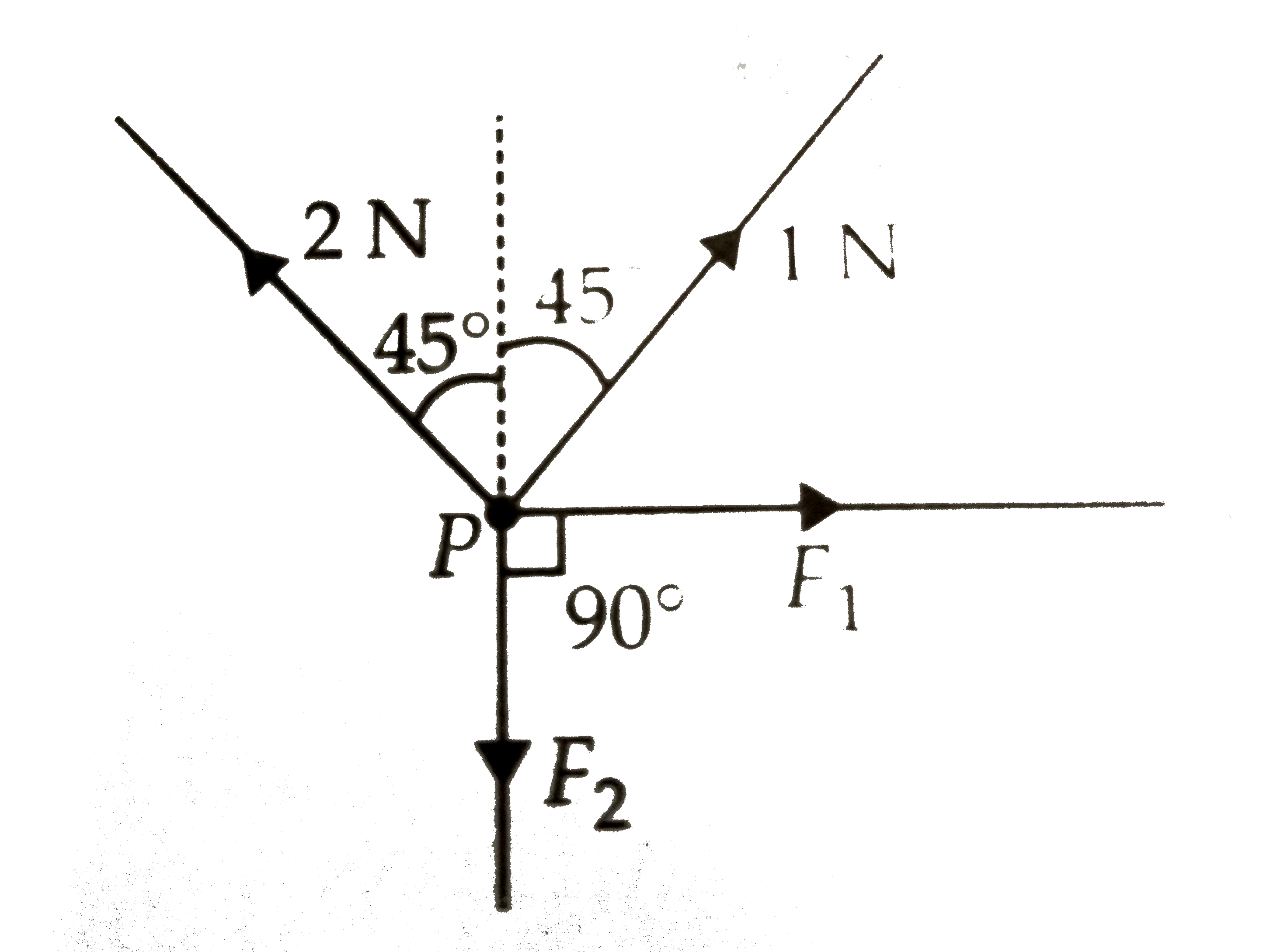
View SolutionA wheel of radius R with an axle of radius R/2 is shown in the figure and is free to rotate about a frictionless axis through its centre and perpendicular to the page. Three forces (F, F, 2F) are exerted tangentially to the repective rims as shown in the figure.
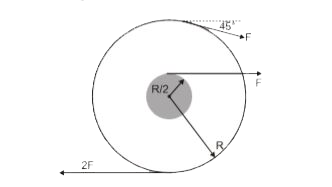
The magnitude of the net torque acting on the system is nearly
View Solution
