At the moment t=0, a force F=kt (k is a constant) is applied to a small body of mass m resting on a smooth horizontal plane . The permanent direction of force F , makes an angle β with the gorizontal . Calculate
(i) The velocity of the body at the moment of its breaking off the plane .
(ii) The distance traversed by the body upto this moment .

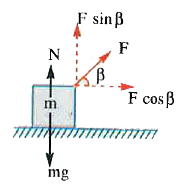
The free body diagram of mass m is shown in figure . For vertical equlibrium
Fsinβ+N=mg(or)AsF=kt
∴Ktsinβ+N=mg…..(1)
Equation of motion of mass m is Fcosβ=ma
or ktcosβ=mdvdt(asa=dvdt),dv=dtcosβdt
Integrating ∫v0dv=kmcosβ∫t0tdt
[v]v0=kmcosβ[t22]t0⇒v=kcosβ2mt2 ....(2)
At the moment of breaking off the plane N=0.if τ is the corresponding time , then <br>:. "From" (1) k tau sin beta =mg "or" tau=(mg)/(k sin beta)....(3)<br>:. Thevelocityatthemomentofbreak∈goffthepla≠isgivenbypu∈gt=tau ∈equation(2),so(v=v_(0))<br>v_(0)=(k cos beta)/(2m) tau^(2)=(k cos beta)/(2m)((mg)/(k sin beta))^(2)<br>:. v_(0)=(mg^(2) cos beta)/(2k sin^(2) beta)<br>(b)Equation(2)maybeexpressedas(dx)/(dt)=(k cos beta )/(2m) t^(2)<br>Integrat∈g[x]_(0)^(x)=(k cos beta)/(2m)[t^(3)/3]_(0)^(t)<br>:. x=(k cos beta)/(6m)t^(3)<br>Whenthebodybreaksoffthepla≠,wehave<br>:. x_(0)=(k cos beta)/(6m) ((mg)/(k sin beta))^(3) =(m^(2)g^(3) cos beta )/(6k^(2) sin ^(3) beta)
Similar Questions
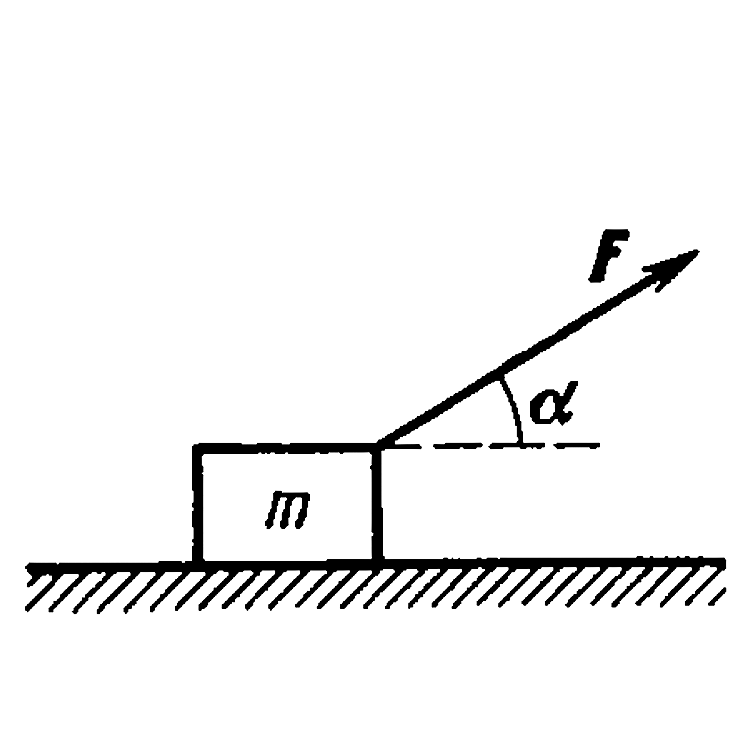
At the moment t=0 the force F=at is applied to a small body of mass m resting on a smooth horizontal plane (a is constant).
The permanent direction of this force forms an angle α with the horizontal (figure). Find:
(a) the velocity of the body at the moment of its breaking off the plane,
(b) the distance traversed by the body up to this moment.
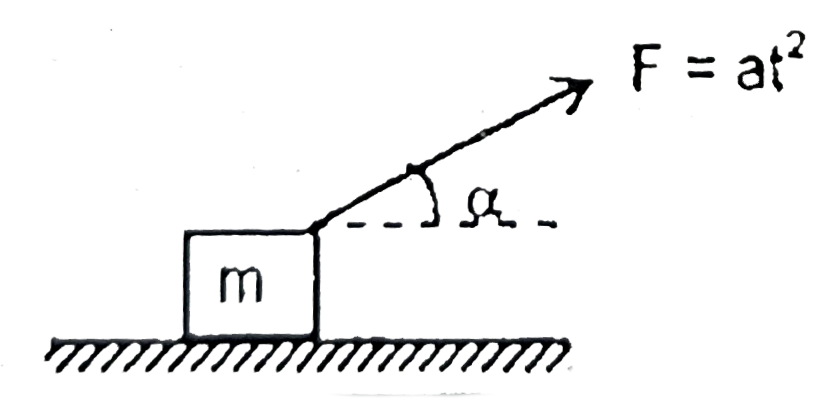
View SolutionAt t=0, a force F=at2 is applied to a small body of mass m at an angle α resting on a smooth horizontal plane
View Solution
Knowledge Check
At t=0, a force F=at2 is applied to s small body of mass m at an angle α resting on a smooth horizontal plane.
 AVelocity of the body at the moment it breaks off the plane is √mg39atan2αsinαBThe distance travelled by the body before breaking off the plane is mg212asinαtanαCIts acceleration at the time of breaking off the plane is gcotα.DTime at which it breaks off the plane is √mgasinα
AVelocity of the body at the moment it breaks off the plane is √mg39atan2αsinαBThe distance travelled by the body before breaking off the plane is mg212asinαtanαCIts acceleration at the time of breaking off the plane is gcotα.DTime at which it breaks off the plane is √mgasinαAt the moment t=0 force F=kt is applied to a small body of mass m resting on a smooth horizontal plane (k is a constant) The direction of this force always forms an angle θ with the horizontal as shown.
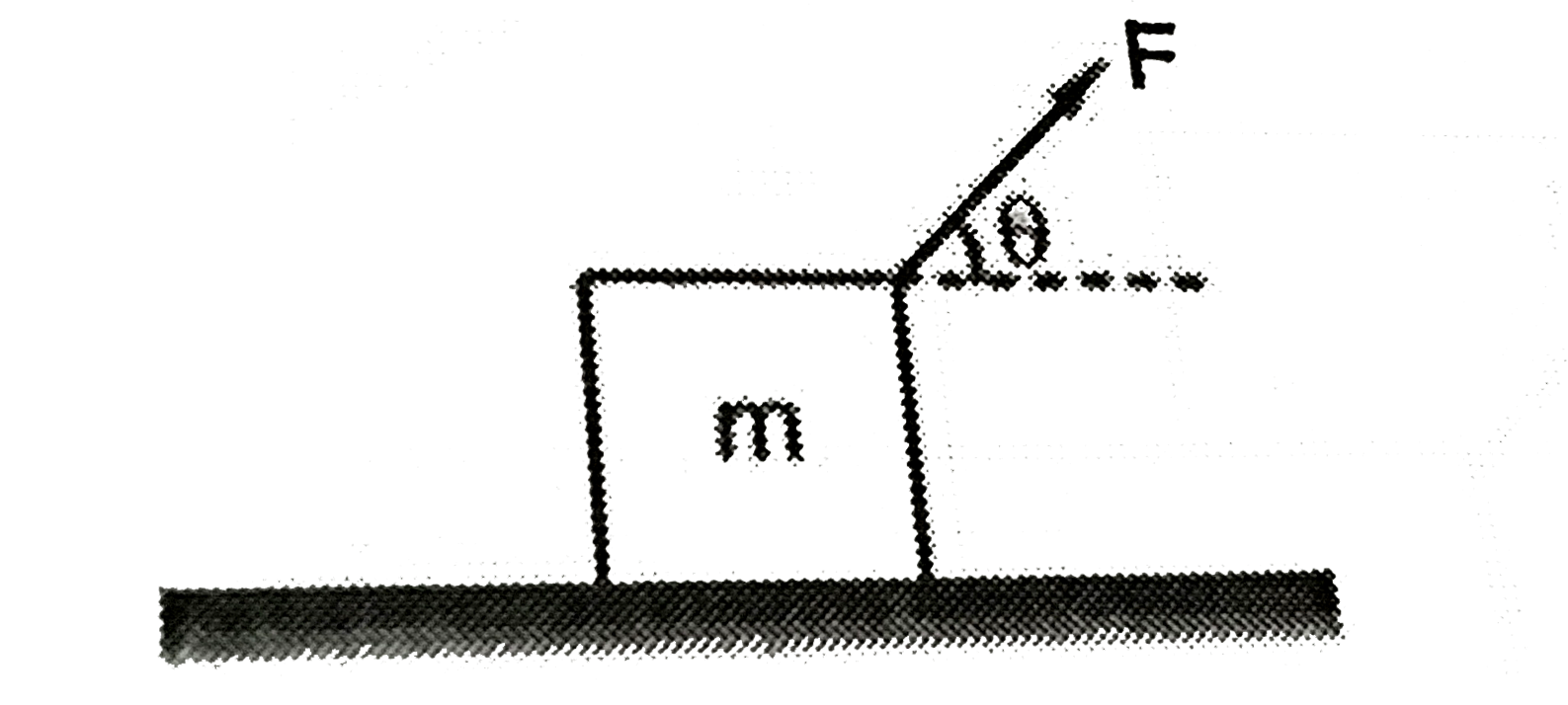
Find the time t at which moment, the body breaks off the plane:Amg2ksinθBmgksinθCmgksin2θD2mgksinθA force of 20N is applied on a body of mass 5 kg resting on a horizontal plane. The body gains a kinetic energy of 10 after is moves a distance 2m. The fricitional force is
A10NB15NC20ND30N
At the instant t=0, a force F=kt (k is a constant) acts on a small body of mass m resting on a smooth horizontal surface. The time, when the body leaves the surface is
View SolutionAt the instant t=0, a force F=kt (k is a constant) acts on a small body of mass m resting on a smooth horizontal surface. The time, when the body leaves the surface is

View SolutionAt the moment t = 0 , the force F = kt is applied to a small body of mass 'm' resting on a smoth horizontal plane. (K is a positive constant ). The direction of the force an angle θ with the horizontal always as shown

The distance travelled x by the body along horizontal before it leaves contact with the horizontal at t=t0 can be expressed in relation with time 't' as
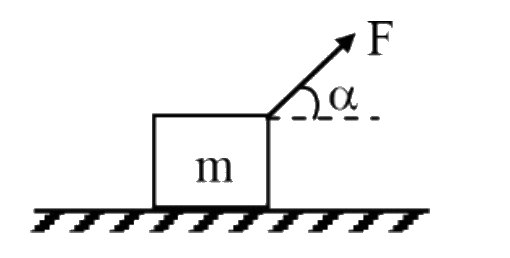
View SolutionAt t=0, a force F = kt is applied on a block of mass m making an angle α with the horizontal . Suppose surfaces to be smooth. Find the velocity of the body at the time of breaking off the plane.

View SolutionAt t=0, a force F = kt is applied on a block of mass m making an angle α with the horizontal . Suppose surfaces to be smooth. Find the velocity of the body at the time of breaking off the plane.

View Solution
