An ant is at a corner of a cubical room of side a. The ant can move with a constant speed u. The minimum time taken to reach the farthest corner of the cube is
3au
√3au
√5au
(√2+1)au
The correct Answer is:C
To solve the problem of finding the minimum time taken for an ant to travel from one corner of a cubical room to the farthest corner, we can follow these steps:
1. Understanding the Problem:
- The ant starts at one corner of a cube and needs to reach the opposite corner. The cube has a side length of a.
2. Identifying the Corners:
- Let's denote the starting corner as point P and the farthest corner as point R.
3. Visualizing the Cube:
- If we visualize or unfold the cube, we can see that the shortest path from P to R can be represented as a straight line across the unfolded surface of the cube.
4. Finding the Shortest Path:
- The distance between the two corners can be calculated using the Pythagorean theorem.
- The straight-line distance d from point P to point R can be represented as the hypotenuse of a right triangle formed by two edges of the cube.
- The distance can be calculated as:
d=√(a2+a2+a2)=√3a2=a√3
5. Calculating the Minimum Time:
- The time t taken to travel this distance at a constant speed u is given by the formula:
t=distancespeed=du
- Substituting the distance we found:
t=a√3u
6. Final Result:
- Therefore, the minimum time taken for the ant to reach the farthest corner of the cube is:
t=a√3u
Conclusion:
The minimum time taken for the ant to reach the farthest corner of the cube is a√3u.
- The ant starts at one corner of a cube and needs to reach the opposite corner. The cube has a side length of a.
- Let's denote the starting corner as point P and the farthest corner as point R.
- If we visualize or unfold the cube, we can see that the shortest path from P to R can be represented as a straight line across the unfolded surface of the cube.
- The distance between the two corners can be calculated using the Pythagorean theorem.
- The straight-line distance d from point P to point R can be represented as the hypotenuse of a right triangle formed by two edges of the cube.
- The distance can be calculated as:
d=√(a2+a2+a2)=√3a2=a√3
- The time t taken to travel this distance at a constant speed u is given by the formula:
t=distancespeed=du
- Substituting the distance we found:
t=a√3u
- Therefore, the minimum time taken for the ant to reach the farthest corner of the cube is:
t=a√3u
The minimum time taken for the ant to reach the farthest corner of the cube is a√3u.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Subjective50videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - More Than One Correct6videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Assertion And Reason12videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
Six particles situated at the corners of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
View SolutionFigure shows an imaginary cube of side a. A uniformly charged rod of length a moves towards right at a constant speed v. At t=0 the right end of the just touches the left face of the cube. Plot a graph between electric flux passing through the cube versus time.
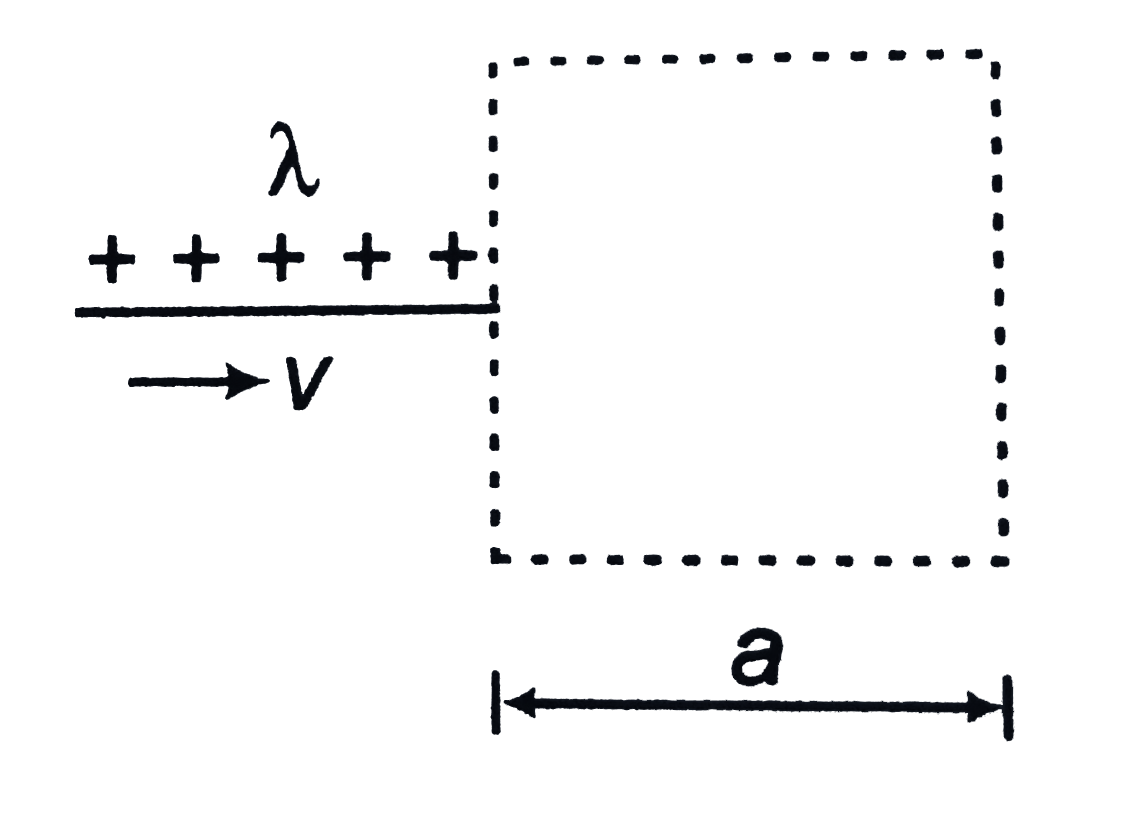 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
From a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is:
AgH = (n−2)u2B2 gH = n2u2CgH = (n−2)2u2D2 gH = ν2(n−2)
Four persons A, B, C and D initially at the corners of a square of side of length d. If every person starts moving with same speed v such that each one faces the other always, the person will meet after time
View SolutionIn the figure the top view of a compartment of a train is shown. A man is sitting at a corner 'B' of the compartment . The man throws a ball ( with respect to himself ) along the surface of the floor towards the corner 'D' of the compartment of the train. The ball hits the corner 'A' of the compartment, then find the time at which it hits A after the ball is thrown . Assume no other collision during motion and floor is smooth. The length of the compartment is given 'l' and the train is moving with constant acceleration 'a' in the direction shown in the figure.
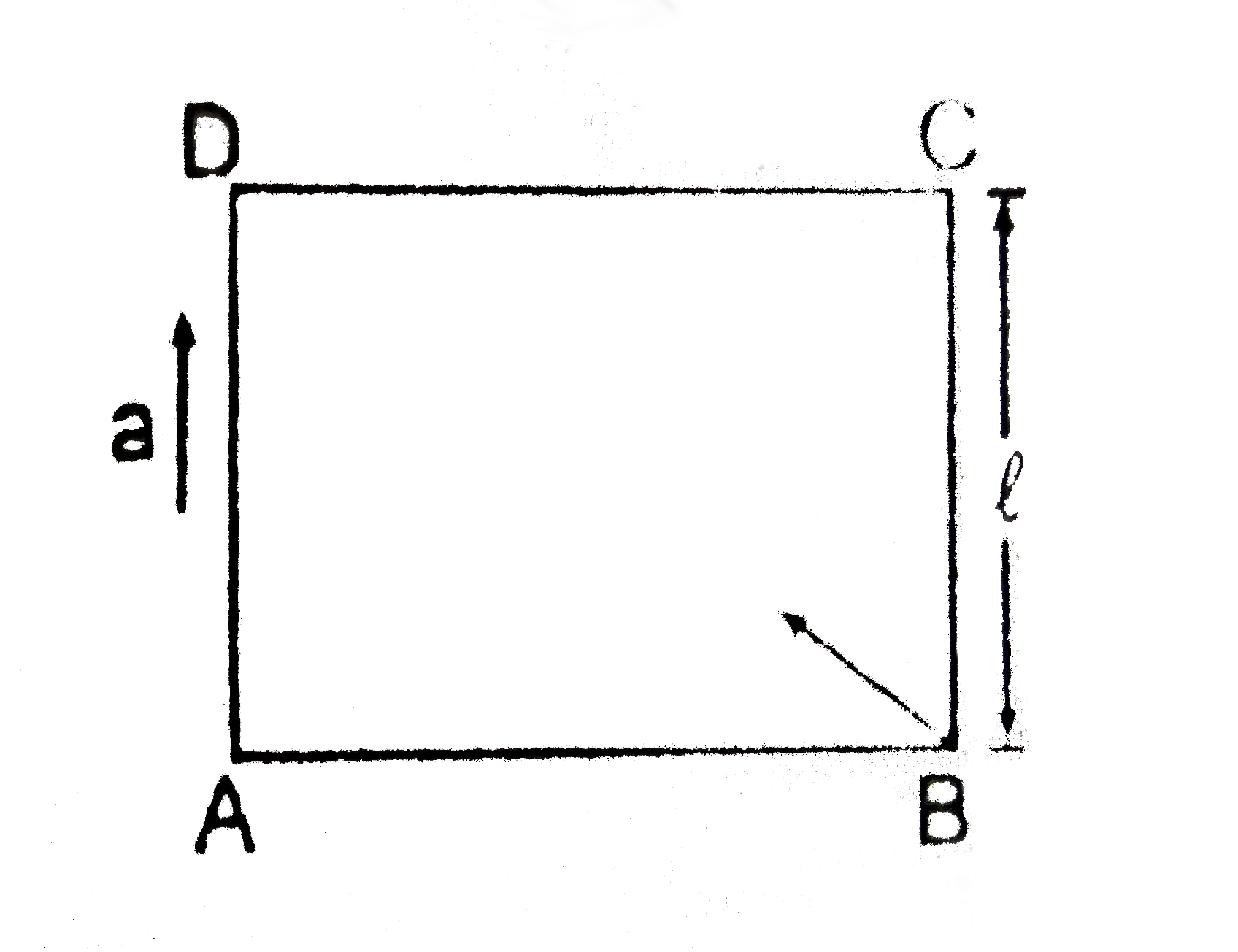 View Solution
View Solution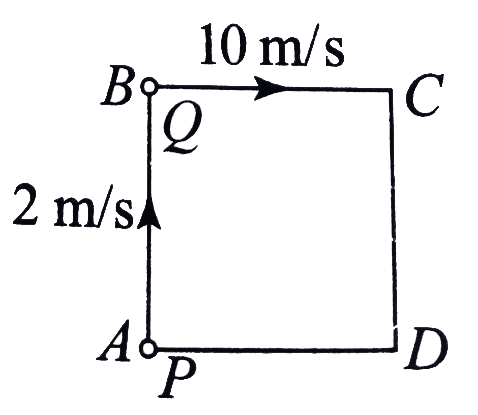
Two men P & Q are standing at corners A & B of square ABCD of side 8m. They start moving along the track with constant speed 2m/s and 10m/s respectively. Find the time when they will meet for the first timeView SolutionFour particles A,B,CandD are situated at the corner of a square ABCD of side a at t-0. Each of particles moves with constant speed (v). A always has its velocity along AB,B along BC,C along CD~andD along DA. At what time will these particles meet each other ?
View SolutionA body is projected up with a speed u and the time taken by it is T to reach the maximum height H. Pich out the correct statement
View SolutionFrom a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is
View Solution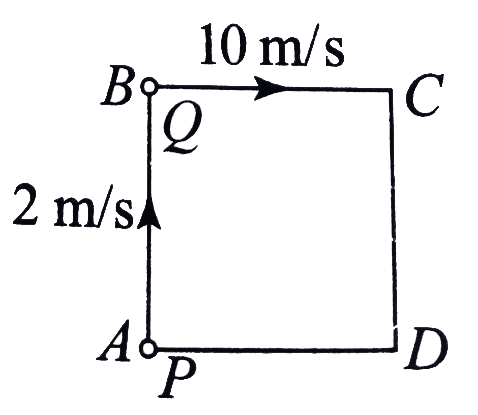
Two men P & Q are standing at corners A & B of square ABCD of side 8m. They start moving along the track with constant speed 2ms and 10ms respectively. Find the time when they will meet for the first timeView Solution

