A horizontal force F=mg3 is applied on the upper surface of a uniform cube of mass m and slide a which is resting on a rough horizontal surface having μ=12. The distance between lines of action of mg and normal reation is
a2
a3
a4
None of these
The correct Answer is:B
To solve the problem, we need to determine the distance x between the line of action of the gravitational force mg and the normal reaction force N acting on the cube. Let's break down the solution step by step.
Step 1: Identify the forces acting on the cube
The forces acting on the cube are:
- The gravitational force mg acting downward at the center of mass of the cube.
- The normal force N acting upward.
- The applied horizontal force F=mg3.
- The frictional force f acting in the opposite direction of the applied force.
Step 2: Determine the frictional force
Since the cube is resting and not sliding, the frictional force f must balance the applied force F. Therefore:
f=F=mg3
Step 3: Set up the moment balance about point C
Let’s consider point C as the center of the cube. The moment due to the normal force N and the moment due to the applied force F must balance each other about point C. The distance from point C to the line of action of the normal force is x, and the distance from point C to the line of action of the applied force F is a2 (where a is the side length of the cube).
The moment balance equation can be expressed as:
N⋅x=F⋅a2
Step 4: Substitute the known values
We know that F=mg3. Therefore, substituting this into the moment balance equation gives:
N⋅x=(mg3)⋅a2
Step 5: Determine the normal force
The normal force N can be determined from the equilibrium of vertical forces. Since the cube is not accelerating vertically:
N=mg
Step 6: Substitute N into the moment balance equation
Now substituting N=mg into the moment balance equation:
mg⋅x=(mg3)⋅a2
Step 7: Simplify the equation
We can cancel mg from both sides (assuming m≠0):
x=13⋅a2
x=a6
Step 8: Conclusion
Thus, the distance x between the line of action of mg and the normal reaction N is:
a6
The forces acting on the cube are:
- The gravitational force mg acting downward at the center of mass of the cube.
- The normal force N acting upward.
- The applied horizontal force F=mg3.
- The frictional force f acting in the opposite direction of the applied force.
Since the cube is resting and not sliding, the frictional force f must balance the applied force F. Therefore:
f=F=mg3
Let’s consider point C as the center of the cube. The moment due to the normal force N and the moment due to the applied force F must balance each other about point C. The distance from point C to the line of action of the normal force is x, and the distance from point C to the line of action of the applied force F is a2 (where a is the side length of the cube).
N⋅x=F⋅a2
We know that F=mg3. Therefore, substituting this into the moment balance equation gives:
N⋅x=(mg3)⋅a2
The normal force N can be determined from the equilibrium of vertical forces. Since the cube is not accelerating vertically:
N=mg
Now substituting N=mg into the moment balance equation:
mg⋅x=(mg3)⋅a2
We can cancel mg from both sides (assuming m≠0):
x=13⋅a2
x=a6
Thus, the distance x between the line of action of mg and the normal reaction N is:
a6
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question
32 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
28 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A uniform cube of mass m and slidea is resting in equilibrium on a rough 45∘ inclined surface. The distance point of application of normal reation measured from the lower edge of the cube is
View SolutionA force (F=Mg) is applied on the top of a circular ring of mass M and radius R kept on a rough horizontal surface. If the ring rolls without slipping, then minimum coefficient of friction required is
_PHY_E05_236_Q01.png)
View SolutionA constant horizontal force of 5N in magnitude is applied tangentially to the top most of a ring of mass 10 kg and radius 10 cm kept on a rough horizontal surface with coefficient of friction between surface and ring being 0.2. The friction force on the ring would be: (g=10m/s2)
View SolutionA block of mass m is pulled slowly by a minimum constant force on a rough (μ) horizontal surface through a distance x. Find work done by force F.
View SolutionA block is sliding on a rough horizontal surface. If the contact force on the block is √2 times the frictional force, the coefficient of friction is
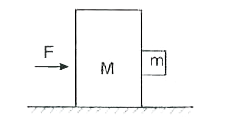
View SolutionA horizontal force F pushes wedge of mass M on a smooth horizontal surface. A block of mass m is stationary to the wedge, then:
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
View SolutionA block of mass 1 kg is held at rest against a rough vertical surface by pushing by a force F horizontally. The coefficient of friction is 0.5. When

View Solution
