A 0.5kg block slides from the point A on a horizontal track with an initial speed 3m/s towards a weightless horizontal spring of length 1m and force constant 2N/m. The part AB of the track is frictionless and the part BC has the confficient of static and kinetic friction as 0.20 respectively. If the distancences AB and BD are 2m and 2.14m respectively, find total distance through which the block moves before it comes to rest completely. (g=10 m//s^(2) ).
The correct Answer is:B, D
To solve the problem step by step, we will analyze the motion of the block from point A to point D, taking into account the effects of friction and the spring.
Step 1: Calculate the initial kinetic energy at point A
The initial kinetic energy (KE) of the block can be calculated using the formula:
KE=12mv2
Where:
- m=0.5kg (mass of the block)
- v=3m/s (initial speed)
Substituting the values:
KE=12×0.5×(3)2=12×0.5×9=2.25J
Step 2: Calculate the work done against friction on path BD
The work done against friction can be calculated using the formula:
W=μkmgd
Where:
- μk=0.2 (coefficient of kinetic friction)
- g=10m/s2 (acceleration due to gravity)
- d=2.14m (distance on path BD)
Substituting the values:
W=0.2×0.5×10×2.14=2.14J
Step 3: Calculate the kinetic energy at point D
The kinetic energy at point D can be found by subtracting the work done against friction from the initial kinetic energy:
KED=KE−W=2.25J−2.14J=0.11J
Step 4: Determine the compression of the spring
When the block compresses the spring, the kinetic energy will be converted into spring potential energy and work done against friction. The energy conservation equation can be written as:
KED=12kx2+μkmgx
Where:
- k=2N/m (spring constant)
- x is the compression of the spring.
Substituting the known values:
0.11=12×2×x2+0.2×0.5×10×x
This simplifies to:
0.11=x2+x
Rearranging gives:
x2+x−0.11=0
Step 5: Solve the quadratic equation for x
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=1,b=1,c=−0.11.
x=−1±√12−4⋅1⋅(−0.11)2⋅1=−1±√1+0.442=−1±√1.442
Calculating the square root:
√1.44=1.2
Thus:
x=−1+1.22=0.22=0.1m
(The negative root is not physically meaningful in this context.)
Step 6: Calculate the total distance moved by the block
The total distance moved by the block is the sum of the distances AB, BD, and the compression of the spring:
Total distance=AB+BD+x=2+2.14+0.1=4.24m
Final Answer
The total distance through which the block moves before it comes to rest completely is 4.24 m.
---
The initial kinetic energy (KE) of the block can be calculated using the formula:
KE=12mv2
Where:
- m=0.5kg (mass of the block)
- v=3m/s (initial speed)
KE=12×0.5×(3)2=12×0.5×9=2.25J
The work done against friction can be calculated using the formula:
W=μkmgd
Where:
- μk=0.2 (coefficient of kinetic friction)
- g=10m/s2 (acceleration due to gravity)
- d=2.14m (distance on path BD)
W=0.2×0.5×10×2.14=2.14J
The kinetic energy at point D can be found by subtracting the work done against friction from the initial kinetic energy:
KED=KE−W=2.25J−2.14J=0.11J
When the block compresses the spring, the kinetic energy will be converted into spring potential energy and work done against friction. The energy conservation equation can be written as:
KED=12kx2+μkmgx
Where:
- k=2N/m (spring constant)
- x is the compression of the spring.
0.11=12×2×x2+0.2×0.5×10×x
This simplifies to:
0.11=x2+x
Rearranging gives:
x2+x−0.11=0
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=1,b=1,c=−0.11.
x=−1±√12−4⋅1⋅(−0.11)2⋅1=−1±√1+0.442=−1±√1.442
Calculating the square root:
√1.44=1.2
Thus:
x=−1+1.22=0.22=0.1m
(The negative root is not physically meaningful in this context.)
The total distance moved by the block is the sum of the distances AB, BD, and the compression of the spring:
Total distance=AB+BD+x=2+2.14+0.1=4.24m
The total distance through which the block moves before it comes to rest completely is 4.24 m.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - TYPE21videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Miscellaneous Example6videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question11videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
A mass of 0.5kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50N/m The maximum compression of the spring would be.
View SolutionA body of mass 5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface collides with a nearly weightless spring of force constant k = 5 N/m. The maximum compression of the spring would be
 View Solution
View SolutionA 16kg block moving on a frictionless horizontal surface with a velocity of 4m/s compresses an ideal spring and comes to rest. If the force constant of the spring be 100N/m, then how much is the spring commpressed ?
View SolutionA particle slides along a track with elevated ends and a flat central part as shown in figure. The flat part has a length l=3m. The curved portions of the track are frictionless. For the flat part, the coefficient of kinetic friction is μk=0.2. The particle is released at point A which is at height h=1.5m above the flat part of the track. Where does the particle finally come to rest?
 View Solution
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
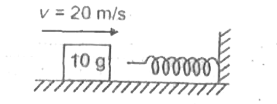 View Solution
View SolutionA block of mass 5 kg is placed on a rough horizontal plane . The coefficients of stastic and kinetic friction between the block and surface are 0⋅5and0⋅3 respectively. A force of 100 N is applied at an angle 30∘ with the horizontal as shown in the figure . The acceleration of the block will be [ g = 10m/s2]
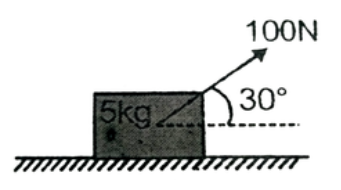 View Solution
View SolutionA body of mass 2kg collides with a horizontal weight spring of force constant 4Nm−1. The body compresses the spring by 1m from rest position. Find the speed of the block at the instant of collision ? Given that the coefficient of kinetic friction between the body and the surface is 0.1.
View SolutionA block of mass 20kg is pushed with a horizontal force of 90N. If the coefficient of static & kinetic friction are 0.4 & 0.3, the frictional force acting on the block is: (g=10ms−2)
View SolutionIn the arrangement show in figure, the track is frictionless until the body reaches the higher level. A frictional force stops the body in a distance d from A. The initial speed of the body v0 is 6 m/s the height h is 1 m and the coefficient of kinetic friction is 0.2.
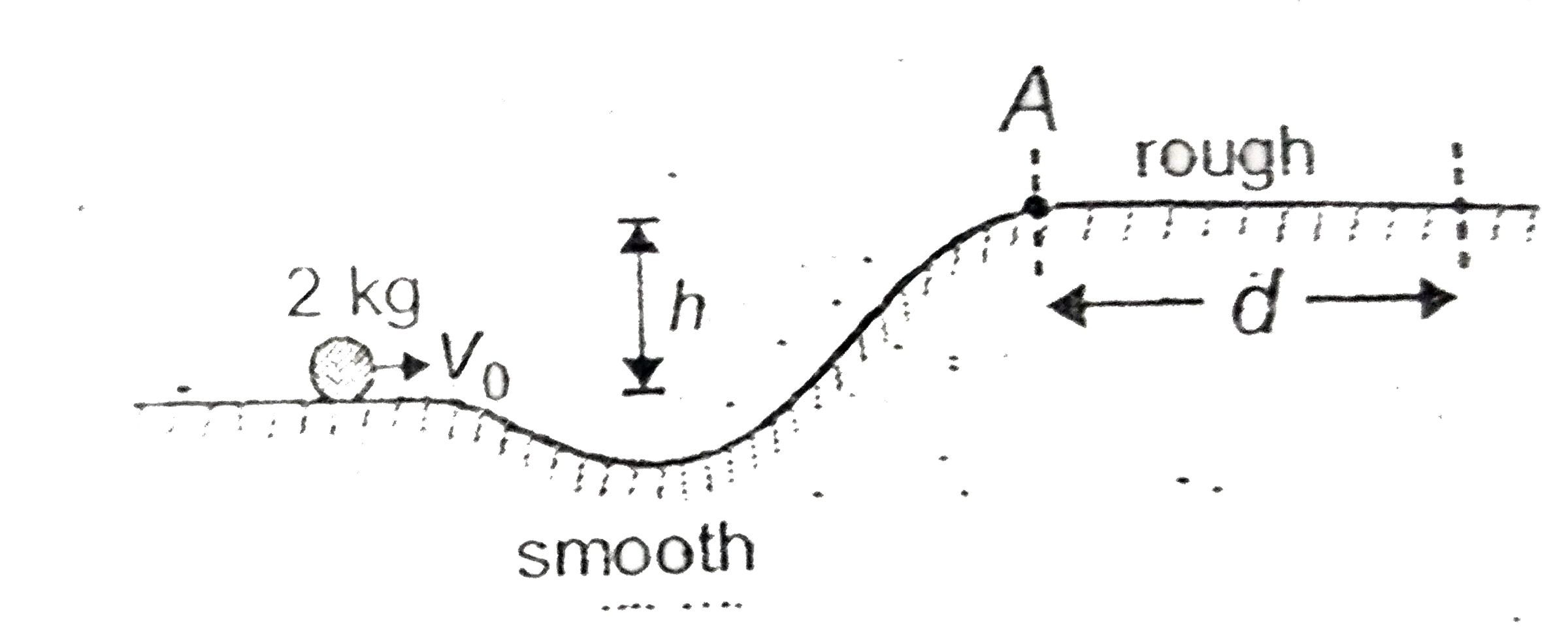
The speed of body at the higher level A isView Solution

