A smooth narrow tube in the form of an arc AB of a circle of centre O and radius r is fixed so that A is vertically above O and OB is horizontal. Particles P of mass m and Q of mass 2 m with a light inextensible string of length (pi r//2) connecting them are placed inside the rube with P at A and Q at B and released from rest. Assuming the string remains taut during motion, find the speed of particles when P reaches B.
 .
.
The correct Answer is:A, B, C
All surfaces are smooth. Therefore, mechanical energy of the system will remain conserved.
∴ Decrease in PE of both the blocks =increase in KE of both blocks
∴(mgr)+(2mg)(πr2)=12(m+2m)v2
or v=√23(1+π)gr.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - TYPE21videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Miscellaneous Example6videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question11videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
A block of mass M is connected with a particle of mass m by a light inextensible string as shown in fig. Assuming all contaction surfaces as smooth, find the acceleration of the wedge after releasing the system.
 View Solution
View SolutionA smooth of mass m1 is lying on a rigid horizontal string A bob of mass m2 hangs from, the ring by an inextensible light string of length l. Find angular frequency of oscillation of the system.
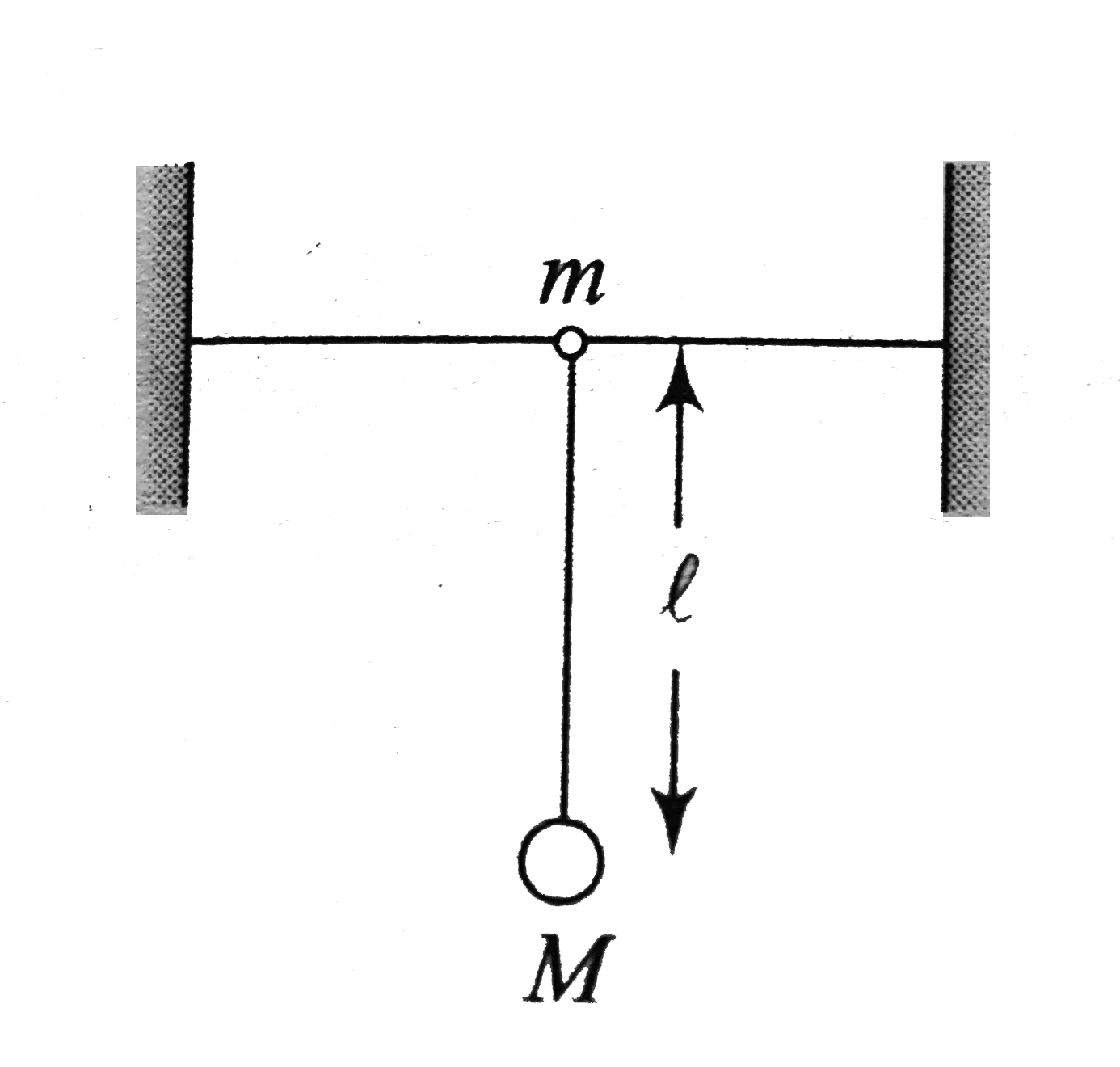 View Solution
View SolutionThree identical particles A, B and C of mass m lie on a smooth horizontal table. Light inextensible strings which are just taut connect AB and BC and ∠ABC is 135° . An impulse J is imparted to the particle C in the direction BC. Mass of each particle is m. Choose the correct options.
 View Solution
View SolutionIf O is the centre of a circle with radius r and AB is a chord of the circle at a distance r2 from O, then ∠BAO=
View SolutionTwo blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is
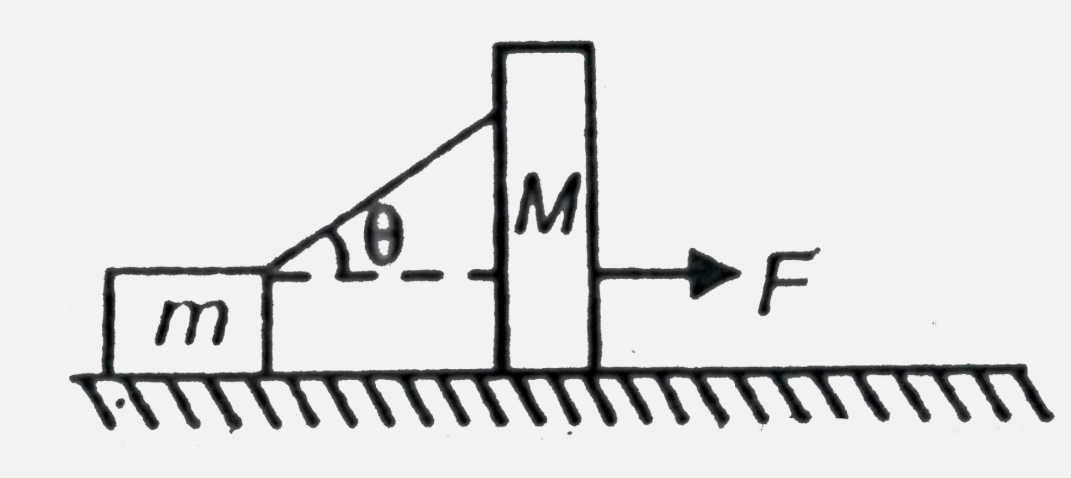 View Solution
View SolutionTwo particles of mass m and 2m are connected by a string of length L and placed at rest over a smooth horizontal surface. The particles are then given velocities as indicated in the figure shown. The tension developed in the string will be
 View Solution
View SolutionA particle of mass m attached to an inextensible light string is moving in a vertical circle of radius r. The critical velocity at the highest point is v0 to complete the vertical circle. The tension in the string when it becomes horizontal is
View Solution∠PQR=100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR
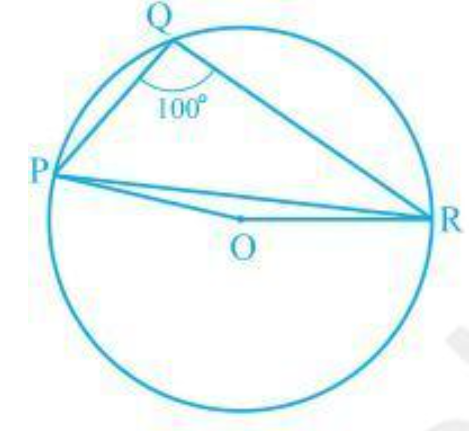 View Solution
View SolutionTwo beads of masses m1andm2 connected by an inextensible string are kept at rest at the horizontal diametrical points of a fixed smooth vertical semicircular tube. If the beads are released from the given position, find their speeds as the function of vertical distance y converted by mass m2.
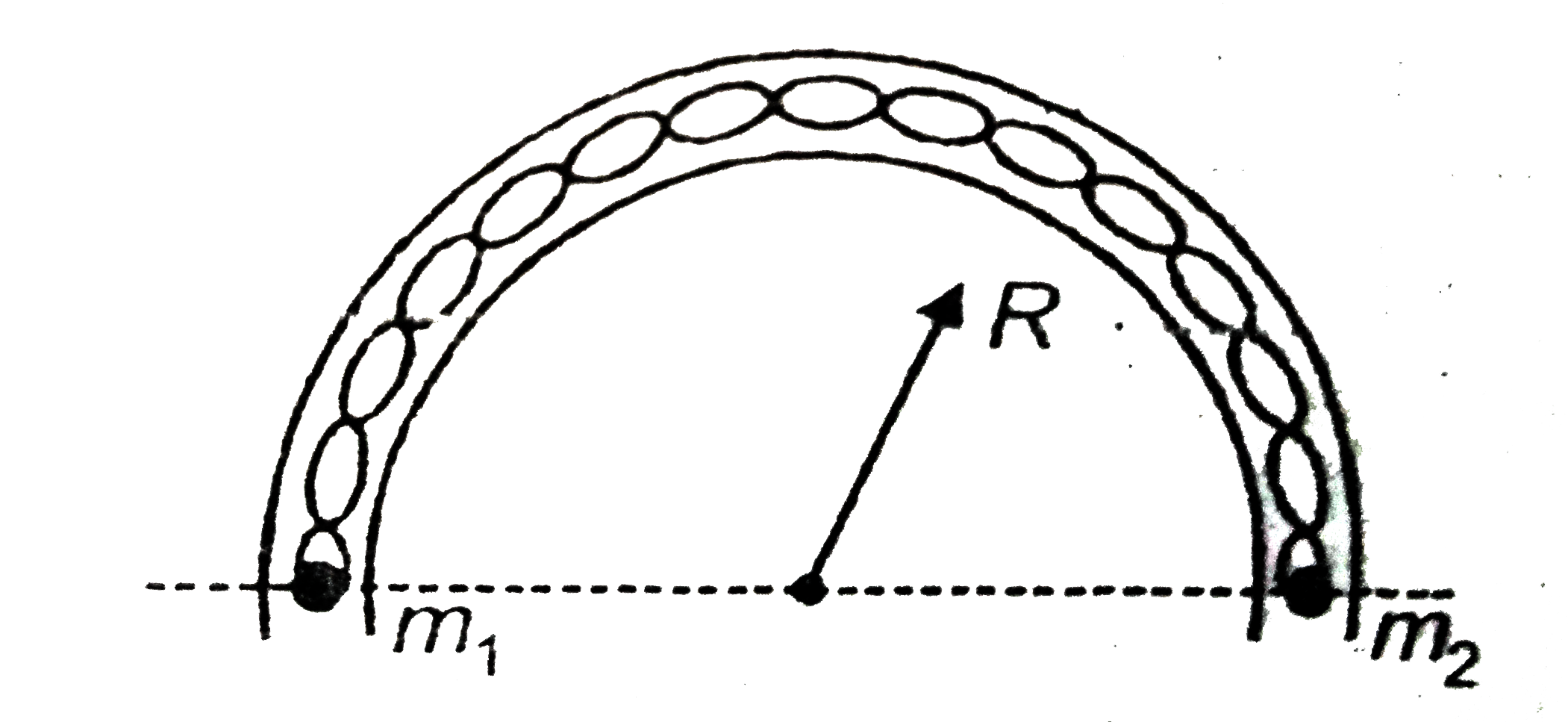 View Solution
View SolutionTwo smooth balls of mass m1 and m2 connected by a light inextensible string are at the opposite points of horizontal diameter of a smooth semi cylindrical surface of radius R. If m1 is released, find its speed at any angular distance θ moved by m2.
 View Solution
View Solution

