Two points A and B are 2 cm apart and a uniform electric field E acts along the straight line AB directed A to B with E=200N/C. A particle of charge +10−6C is taken from A to B along AB, Calculate
a. the force on the charge
b. the potential difference VA−VB and
c.the work done on the charge by E
The correct Answer is:A, B, D
To solve the problem step by step, we will calculate the force on the charge, the potential difference VA−VB, and the work done on the charge by the electric field E.
Given Data:
- Distance between points A and B, d=2cm=0.02m
- Electric field, E=200N/C
- Charge, q=+10−6C
Part (a): Calculate the Force on the Charge
The force F on a charge in an electric field is given by the formula:
F=q⋅E
Substituting the values:
F=(10−6C)⋅(200N/C)=2×10−4N
Part (b): Calculate the Potential Difference VA−VB
The potential difference VA−VB in a uniform electric field is given by:
VA−VB=−E⋅d
Substituting the values:
VA−VB=−(200N/C)⋅(0.02m)=−4V
Thus, the magnitude of the potential difference is 4V.
Part (c): Calculate the Work Done on the Charge by E
The work done W on the charge by the electric field is given by:
W=q⋅(VA−VB)
Substituting the values:
W=(10−6C)⋅(−4V)=−4×10−6J
Summary of Results:
- Force on the charge: 2×10−4N
- Potential difference VA−VB: −4V (or 4V in magnitude)
- Work done on the charge by E: −4×10−6J
- Distance between points A and B, d=2cm=0.02m
- Electric field, E=200N/C
- Charge, q=+10−6C
The force F on a charge in an electric field is given by the formula:
F=q⋅E
Substituting the values:
F=(10−6C)⋅(200N/C)=2×10−4N
The potential difference VA−VB in a uniform electric field is given by:
VA−VB=−E⋅d
Substituting the values:
VA−VB=−(200N/C)⋅(0.02m)=−4V
Thus, the magnitude of the potential difference is 4V.
The work done W on the charge by the electric field is given by:
W=q⋅(VA−VB)
Substituting the values:
W=(10−6C)⋅(−4V)=−4×10−6J
- Force on the charge: 2×10−4N
- Potential difference VA−VB: −4V (or 4V in magnitude)
- Work done on the charge by E: −4×10−6J
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.14videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.29videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 83videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
The work done to move a charge along an equipotential from A to B
View SolutionThe work done to move a charge along an equipotential from A to B
View SolutionThe work done in carrying a charge of 5μC form a point A to a point B in an electric field is 10mJ. The potential difference (VB−VA) is then
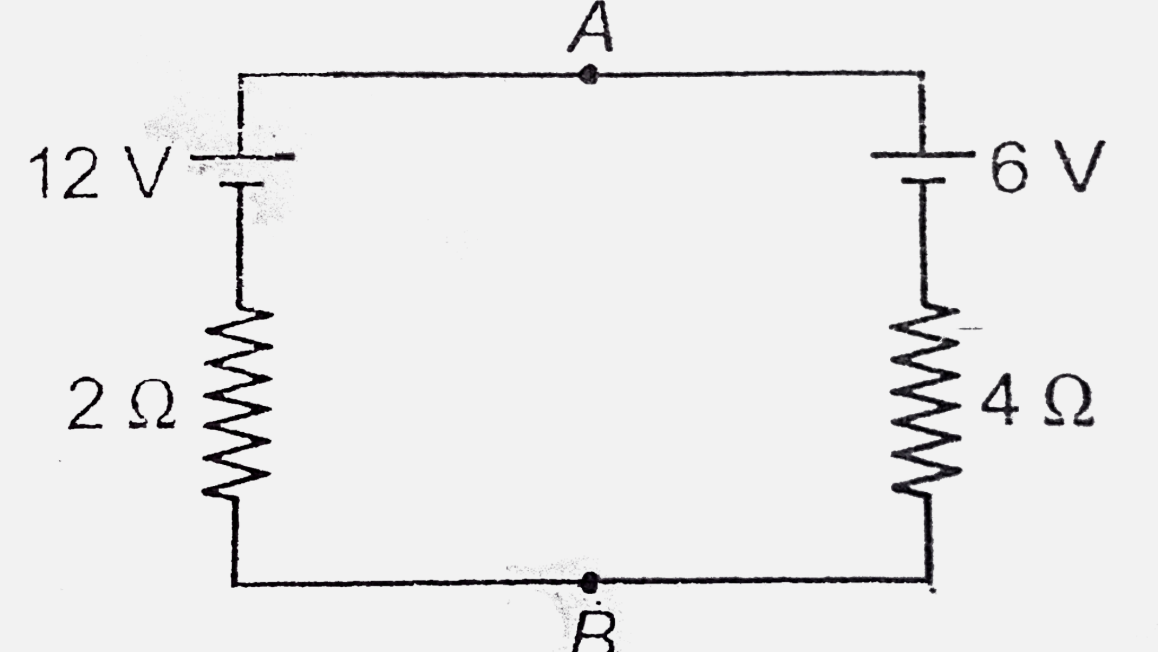
View SolutionPotential difference across AB , i.e., VA−VB is
 View Solution
View SolutionA point charge is taken from a point A to a pint B in an electric field. Does the work done by the electric field depend on the path of the charge ?
View SolutionWhen a 2μC charge is carried from point A to point B, the amount of work done by the electric field is 50μJ. What is the potential difference and which point is at a higher potential ?
View SolutionIn uniform electric field E=10N/C, find

a. VA−VB , b. VB−VCView SolutionTwo point charges qA=3μCandqB=−3μC are located 20cm apart in vacuum. What is the electric field at the mid point of the line joining the two charges.
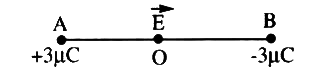 View Solution
View SolutionHow much work is done in moving a charge of 2C across two points having a potential difference of 12V ?
View SolutionIn a certain region, electric field E exists along the x - axis which is uniform. Given AB=2√3m and BC=4m. Points A, B, and C are in xy plane.
 .
.
find the potential difference VC−VB between the points CandB.View Solution

