Question

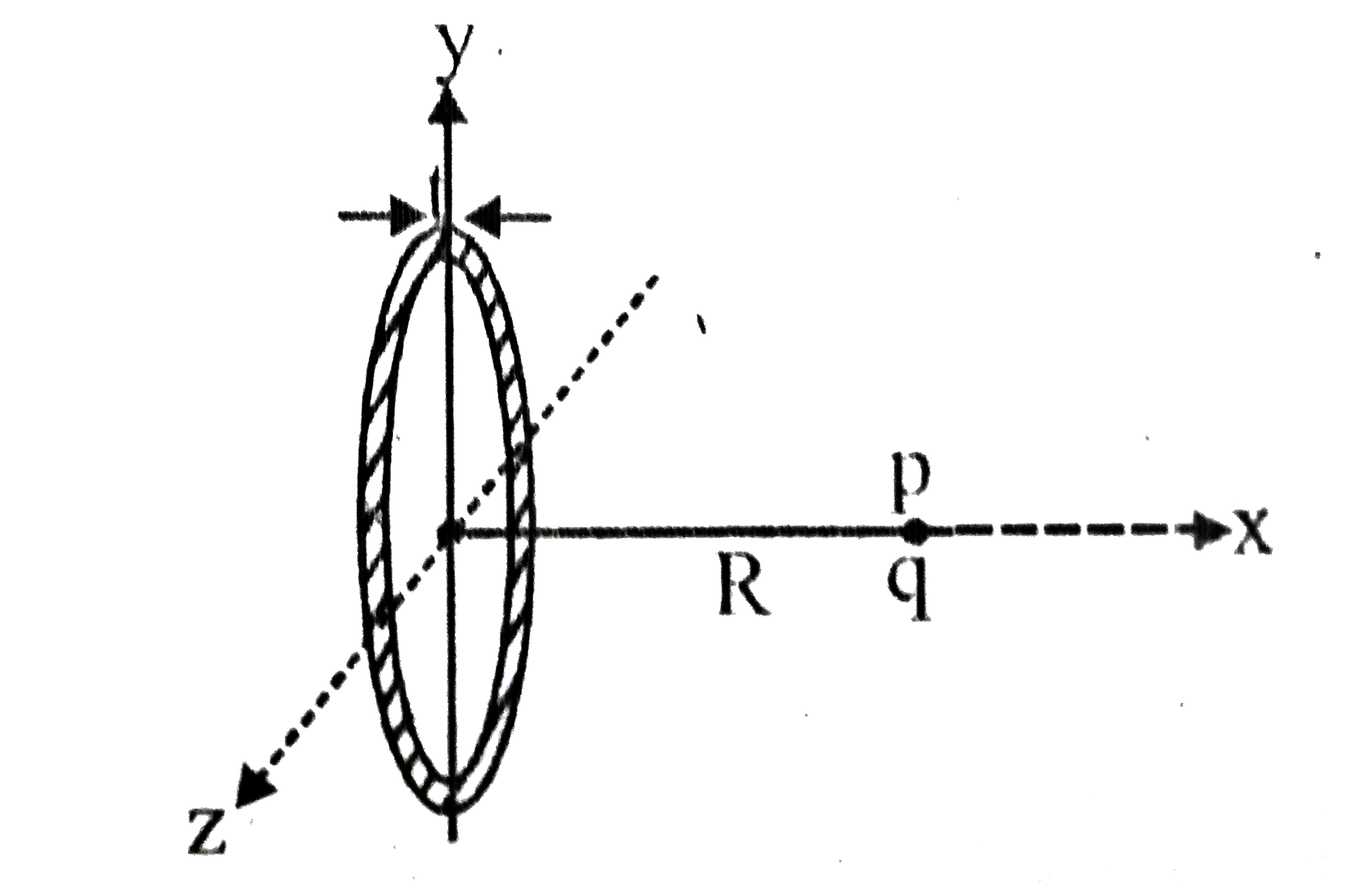
A uniformly charged thin ring has radius $10.0cm$ and total charge $+12.0\mu C$. An electron is placed on the ring's axis a distance $25.0cm$ from the centre of the ring and is constrained to stay on the axis of the ring. The electron is then released from rest.
a. describe the subsequent motion of the electron
b. find the speed of the electron when it reaches the centre of the ring

Answer

A::D

Explanation

To solve the problem step by step, we will break it down into two parts as described in the question.

Part a: Describe the Subsequent Motion of the Electron

1. Understanding the Setup:
- We have a uniformly charged thin ring with a radius of \( R = 10.0 \, \text{cm} = 0.1 \, \text{m} \) and a total charge of \( Q = +12.0 \, \mu\text{C} = 12.0 \times 10^{-6} \, \text{C} \).
- An electron (which has a negative charge) is placed on the axis of the ring at a distance \( X = 25.0 \, \text{cm} = 0.25 \, \text{m} \) from the center of the ring.

2. Electric Field Direction:
- The electric field due to the positively charged ring at the position of the electron will point towards the ring. This is because the electric field lines point away from positive charges.

3. Motion of the Electron:
- When the electron is released from rest, it will experience a force due to the electric field directed towards the ring.
- As the electron moves towards the ring, it will accelerate due to this force.
- Upon reaching the center of the ring, the electric field will still act on the electron, causing it to continue moving past the center and oscillate back and forth along the axis of the ring.

4. Type of Motion:
- The motion of the electron can be described as oscillatory or simple harmonic motion (SHM) about the center of the ring, as it will move towards the ring and then back past the center due to the restoring force exerted by the electric field.

Part b: Find the Speed of the Electron When It Reaches the Center of the Ring

1. Conservation of Energy:
- We can use the conservation of mechanical energy principle, which states that the total mechanical energy (kinetic + potential) remains constant in the absence of non-conservative forces.
- The initial kinetic energy (\( K_i \)) is zero since the electron is released from rest.
- The initial potential energy (\( U_i \)) when the electron is at distance \( X \) from the center can be calculated using the formula for electric potential energy:
\( U_i = k \cdot \frac{Q \cdot (-e)}{r} \)
where \( k \) is Coulomb's constant (\( 9 \times 10^9 \, \text{N m}^2/\text{C}^2 \)), \( Q \) is the charge of the ring, \( e \) is the charge of the electron (\( 1.6 \times 10^{-19} \, \text{C} \)), and \( r \) is the distance from the charge to the electron.

2. Calculating Initial Potential Energy:
- The distance \( r \) from the charge to the electron when it is at point \( P \) is given by:
\( r = \sqrt{R^2 + X^2} = \sqrt{(0.1)^2 + (0.25)^2} = \sqrt{0.01 + 0.0625} = \sqrt{0.0725} \approx 0.269 \, \text{m} \)
- Thus, the initial potential energy is:
\( U_i = k \cdot \frac{Q \cdot (-e)}{r} = 9 \times 10^9 \cdot \frac{(12 \times 10^{-6}) \cdot (-1.6 \times 10^{-19})}{0.269} \)

3. Final Potential Energy at the Center:
- When the electron reaches the center of the ring, the potential energy is:
\( U_f = k \cdot \frac{Q \cdot (-e)}{R} = 9 \times 10^9 \cdot \frac{(12 \times 10^{-6}) \cdot (-1.6 \times 10^{-19})}{0.1} \)

4. Kinetic Energy at the Center:
- The final kinetic energy (\( K_f \)) when the electron reaches the center is given by:
\( K_f = \frac{1}{2} m v^2 \)
- By conservation of energy:
\( K_i + U_i = K_f + U_f \)
- Substituting the values:
\( 0 + U_i = \frac{1}{2} m v^2 + U_f \)

5. Solving for Speed:
- Rearranging gives:
\( \frac{1}{2} m v^2 = U_i - U_f \)
- Solving for \( v \):
\( v = \sqrt{\frac{2(U_i - U_f)}{m}} \)
- Using \( m \) (mass of electron) = \( 9.11 \times 10^{-31} \, \text{kg} \), we can calculate \( v \).

Final Calculation
After substituting the values and simplifying, we find that the speed of the electron when it reaches the center of the ring is approximately:
\( v \approx 15.45 \times 10^6 \, \text{m/s} \)