Two concentric spheres of radii R and 2R are charged. The inner sphere has a charge if 1μC and the outer sphere has a charge of 2μC of the same sigh. The potential is 9000V at a distance 3R from the common centre. The value of R is
1m
2m
3m
4m
The correct Answer is:A
To solve the problem, we need to calculate the value of R given the potential at a distance of 3R from the center of two concentric spheres with known charges.
1. Identify the Charges and Distances:
- The inner sphere has a charge q1=1μC=1×10−6C.
- The outer sphere has a charge q2=2μC=2×10−6C.
- The distance from the center where the potential is measured is r=3R.
2. Formula for Electric Potential:
The electric potential V at a distance r from a point charge q is given by:
V=kqr
where k is Coulomb's constant, k≈9×109N⋅m2/C2.
3. Calculate the Total Potential at Distance 3R:
The total potential V at a distance 3R due to both spheres is the sum of the potentials due to each sphere:
V=V1+V2=kq13R+kq23R
Factoring out k/3R:
V=k3R(q1+q2)
4. Substituting the Values:
Substitute q1 and q2:
V=k3R(1×10−6+2×10−6)=k3R(3×10−6)
5. Set the Potential Equal to the Given Value:
We know from the problem statement that the potential at 3R is 9000V:
k3R(3×10−6)=9000
6. Rearranging the Equation:
Rearranging the equation to solve for R:
R=k⋅3×10−63⋅9000
Simplifying:
R=k⋅10−69000
7. Substituting the Value of k:
Substitute k=9×109:
R=(9×109)⋅(10−6)9000
Simplifying further:
R=9×1039000=1m
Final Answer:
The value of R is 1m.
- The inner sphere has a charge q1=1μC=1×10−6C.
- The outer sphere has a charge q2=2μC=2×10−6C.
- The distance from the center where the potential is measured is r=3R.
The electric potential V at a distance r from a point charge q is given by:
V=kqr
where k is Coulomb's constant, k≈9×109N⋅m2/C2.
The total potential V at a distance 3R due to both spheres is the sum of the potentials due to each sphere:
V=V1+V2=kq13R+kq23R
Factoring out k/3R:
V=k3R(q1+q2)
Substitute q1 and q2:
V=k3R(1×10−6+2×10−6)=k3R(3×10−6)
We know from the problem statement that the potential at 3R is 9000V:
k3R(3×10−6)=9000
Rearranging the equation to solve for R:
R=k⋅3×10−63⋅9000
Simplifying:
R=k⋅10−69000
Substitute k=9×109:
R=(9×109)⋅(10−6)9000
Simplifying further:
R=9×1039000=1m
The value of R is 1m.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective15videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - SUBJECTIVE_TYPE6videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Assertion And Reason19videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
A conducting sphere of radius r has a charge . Then .
View SolutionThere are two concentric hollow conducting spherical shells of radii r and R(R>r). The charge on the outer shell is Q. What charge should be given to the inner shell, so that the potential at a point P , at a distance 2R from the common centre is zero ?
View SolutionThe diameter of a hollow metallic sphere is 60 cm and the sphere carries a charge of 500μC. The potential at a distance of 100cm from the centre of the sphere will be
View SolutionTwo concentric spheres of radii R and r have similar charges with equal surface charge densities (σ). The electric potential at their common centre is
View SolutionTwo connectric spheres of radii R and r have similar charges with equal surface charge densities (sigam). The electric potential at their common centre is
View SolutionTwo concentric hollow conducting spheres of radius r and R are shown. The charge on outer shell is Q. what charge should be given to inner sphere so that the potential at any point P outside the outer sphere is zero ?
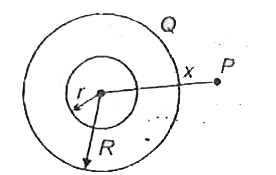 View Solution
View SolutionA spherical capacitor has the inner sphere of radius 2cm and the outerone of 4cm. If the inner sphere is earthed and the outer one is charged with a charge of 2μC and isolated. Calculate ltbr> (a) the potential to which the outer sphere is raised.
(b) the charge retained on the outer surface of the outer sphere.View SolutionTwo spheres of radii R1 and R1 respectively are charged and joined by wire. The ratio of electric field of spheres is
View SolutionA sphere of 4cm radius is suspended within a hollow sphere of 6cm radius. The inner sphere is charged to potential 3 e.s.u. and the outer sphere is earthed. The charge on the inner sphere is
View SolutionA sphere of 4cm radius is suspended within a hollow sphere of 6cm radius. The inner sphere is charged to potential 3 e.s.u. and the outer sphere is earthed. The charge on the inner sphere is
View Solution

