Choose the correct option:
A metre rule, weighing 100 g rests on a table with a part projecting over the edge. Find the length of the part projecting out if a 5 g body hung at the end just tills the rule.
(a) 37.5 cm
(b) 26.8 cm
(c) 40.2 cm
(d) 47.6 cm
To solve the problem, we need to analyze the situation where a meter rule is balanced on a table with a part projecting over the edge, and a small weight is hung at the end of the rule. The goal is to find the length of the part projecting out when the weight causes the rule to tilt.
1. Identify the Given Data:
- Weight of the meter rule (W_rule) = 100 g = 0.1 kg (since we will use SI units)
- Length of the meter rule (L) = 1 m = 100 cm
- Weight of the hanging body (W_body) = 5 g = 0.005 kg
2. Understand the Setup:
- The meter rule is balanced on the table, with a part of it (let's call this length X) projecting over the edge.
- The center of mass of the meter rule is located at its midpoint, which is at 50 cm from one end.
3. Establish the Pivot Point:
- The pivot point (P) is at the edge of the table where the meter rule is resting.
- The distance from the pivot point to the center of mass of the meter rule is (50 cm - X).
4. Set Up the Torque Equation:
- For the meter rule to be in equilibrium just before it tilts, the clockwise torque due to the weight of the hanging body must equal the counterclockwise torque due to the weight of the meter rule.
- Clockwise torque due to the hanging body = W_body * X = 0.005 kg * g * X
- Counterclockwise torque due to the meter rule = W_rule * (50 cm - X) = 0.1 kg * g * (50 - X)
5. Equate the Torques:
0.005g⋅X=0.1g⋅(50−X)
- We can cancel g from both sides (assuming g is not zero):
0.005X=0.1(50−X)
6. Solve for X:
0.005X=5−0.1X
0.005X+0.1X=5
0.105X=5
X=50.105≈47.619cm
7. Final Answer:
- The length of the part projecting out (X) is approximately 47.6 cm.
Conclusion:
The correct option is D) 47.6 cm.
- Weight of the meter rule (W_rule) = 100 g = 0.1 kg (since we will use SI units)
- Length of the meter rule (L) = 1 m = 100 cm
- Weight of the hanging body (W_body) = 5 g = 0.005 kg
- The meter rule is balanced on the table, with a part of it (let's call this length X) projecting over the edge.
- The center of mass of the meter rule is located at its midpoint, which is at 50 cm from one end.
- The pivot point (P) is at the edge of the table where the meter rule is resting.
- The distance from the pivot point to the center of mass of the meter rule is (50 cm - X).
- For the meter rule to be in equilibrium just before it tilts, the clockwise torque due to the weight of the hanging body must equal the counterclockwise torque due to the weight of the meter rule.
- Clockwise torque due to the hanging body = W_body * X = 0.005 kg * g * X
- Counterclockwise torque due to the meter rule = W_rule * (50 cm - X) = 0.1 kg * g * (50 - X)
0.005g⋅X=0.1g⋅(50−X)
- We can cancel g from both sides (assuming g is not zero):
0.005X=0.1(50−X)
0.005X=5−0.1X
0.005X+0.1X=5
0.105X=5
X=50.105≈47.619cm
- The length of the part projecting out (X) is approximately 47.6 cm.
The correct option is D) 47.6 cm.
Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Only one option is correct for JEE Advanced
60 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct
1 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
A rectangular brick is kept on a table with a part of its length projecting out. It remains at rest if thelength projected is slightly less than half the total length but it falls down if the length projected is slightly more than half the total length. Give reason.
View SolutionA uniform rope of length l and mass m lies on a smooth horizontal table with its length perpendicular to the edge of the table and a small part of the rope having over the edge. The rope starts sliding from rest under the weight of the over hanging end. The velocity of the rope when the length of the hanging part is . x
View Solution
Knowledge Check
A uniform chain of length L and mass M is lying on a smooth table and one-third of its length is hanging vertically down over the edge of the table. If g is the acceleration due to gravity, the work required to pull the hanging part on to the table is
AMgLBMgL3CMgL9DMgL18
A uniform meter scale of mass 1kg is placed on table such that a part of the scale is beyond the edge. If a body of mass 0.25kg is hung at the end of the scale then the minimum length of scale that should lie on the table so that it does not tilt is
View SolutionA track consists of two circular pars ABC and CDE of equal radius 100 m and joined smoothly as shown in figure.Each part subtends a right angle at its centre. A cycle weighing 100 kg together with rider travels at a constant speed of 18 km/h on the track. A. Find the normal contact force by the road on the cycle when it is at B and at D. b.Find the force of friction exerted by the track on the tyres when the cycle is at B,C and D. c. Find the normal force between the road and the cycle just before and just after the cycle crosses C. d. What should be the minimum friction coefficient between the road and the tyre, which will ensure that the cyclist can move with constant speed? Take g=10ms2

View SolutionThe diagram alongside shows a uniform metre rule of weight 100 gf being balanced on a knife edge placed at the 40 cm mark, by suspending a weight w gf at the mark 20 cm, find:
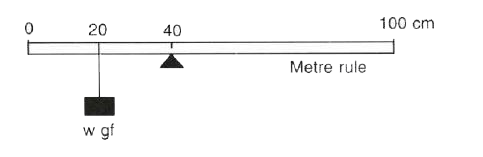
the position of another weight of 50 gf to balance the rule in part (ii).
View SolutionA very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
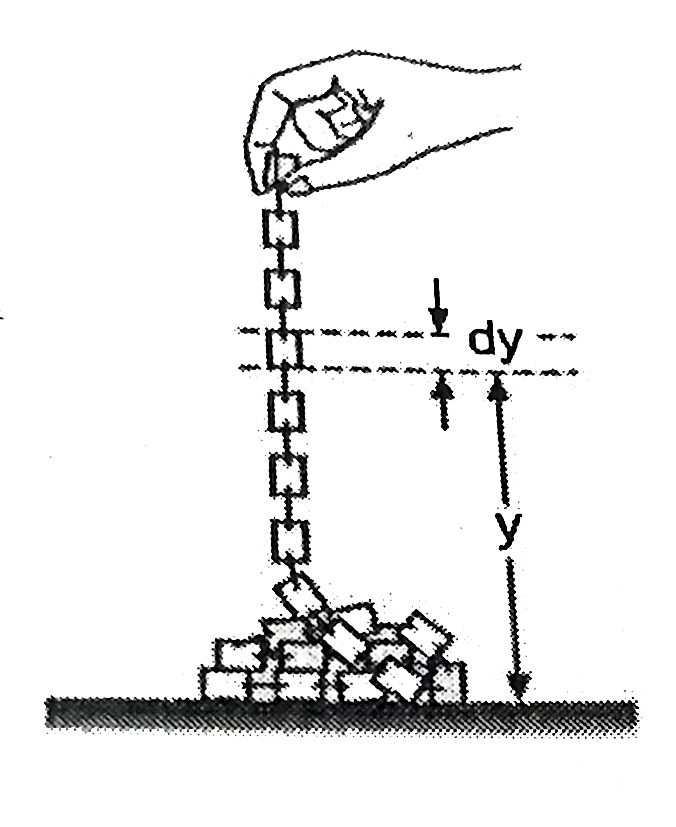
View SolutionA weightless rigid rod AB of length / connects two equal masses m one particle is fixed at the end B and the other at the middle ofthe rod as shown in the figure-5.131. The rod can rotate in the vertical plane freely around the hinge point/4. Choose the correct option(s)
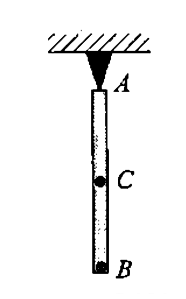
A. The minimum horizontal velocity required to be given to the particle B so as to make the rod go around in the complete vertical circle is √24gl5
B. The minimum horizontal velocity required to be given to the particle B so as to make the rod go around in the complete vertical circle is √24glg
C. The ratio of compressive force in the rods AC and BC is 2:1 when the masses are at highest point.
D. The ratio of compressive force in the rods AC and BC is 3:1 when the masses are at highest point.
View SolutionA 2 kg block A is attached to one end of a light string that passes over an an ideal pulley and a 1 kg sleeve B slides down the other part of the string with an acceleration of 5m/s2 with respect to the string. Find the acceleration of the block, acceleration of sleeve and tension in the steing. [g=10m/s2]

View SolutionA track consists of two circular pars ABC andCDE of equal rdius 100 m and joined smoothly as shown in figure.Each part sutends a right ngle at its centre. A cycle weighing 100 kg together with rider travels at a constant speed of 18 km/h on the track. A. Findteh nromal contct force by tehroad on the cycle whenit is at B and at D. b.Findteh force of friction exerted by the track on the tyres when the cycle is at B,C and D. c. Find the normal force between teh road and teh cycle just before and just after the cycle crosses C. d. What should be the minimum friction coefficient between the road and the tyre, which will ensure that teh cyclist can move with constant speed? Take g=10ms2

View Solution
