Electric potential is a scalar quantity. Due to a point charge charge q at distance r, the potential is given by V=q4π∈0r. A point charge q is placed at (3a,0) and another charge −2q is placed at (−3a,0).
If we plot a graph of potential (V) on x-axis it will be like:




The correct Answer is:D
To solve the problem of finding the electric potential due to two point charges, we will follow these steps:
1. Identify the Charges and Their Positions:
- We have a point charge q located at (3a,0).
- We have another point charge −2q located at (−3a,0).
2. Write the Expression for Electric Potential:
- The electric potential V at a point due to a point charge Q at a distance r is given by:
V=Q4πϵ0r
3. Calculate the Total Potential at a Point x:
- The total potential V at a point x on the x-axis due to both charges can be calculated by summing the potentials due to each charge:
V(x)=Vq+V−2q
- The distance from the charge q at (3a,0) to the point x is |x−3a|.
- The distance from the charge −2q at (−3a,0) to the point x is |x+3a|.
- Therefore, the potential at point x is:
V(x)=q4πϵ0|x−3a|+−2q4πϵ0|x+3a|
4. Set Up the Equation for Zero Potential:
- To find the points where the potential is zero, we set:
q|x−3a|=2q|x+3a|
- Simplifying this gives:
|x−3a|=2|x+3a|
5. Solve for x:
- We will consider two cases based on the absolute values:
- Case 1: x−3a=2(x+3a)
x−3a=2x+6a⟹−x=9a⟹x=−9a
- Case 2: −(x−3a)=2(x+3a)
−x+3a=2x+6a⟹3a−6a=3x⟹−3a=3x⟹x=−a
6. Graphing the Potential:
- The potential will be positive near the positive charge q and negative near the negative charge −2q.
- The potential will approach infinity as we get close to the charges and will cross zero at the points found above.
Final Graph Description:
- The graph of potential V versus position x will show:
- A steep rise towards positive infinity as x approaches 3a from the left.
- A drop to zero at x=−a.
- A steep drop to negative infinity as x approaches −3a from the right.
- The potential will also cross zero at x=−9a.
- We have a point charge q located at (3a,0).
- We have another point charge −2q located at (−3a,0).
- The electric potential V at a point due to a point charge Q at a distance r is given by:
V=Q4πϵ0r
- The total potential V at a point x on the x-axis due to both charges can be calculated by summing the potentials due to each charge:
V(x)=Vq+V−2q
- The distance from the charge q at (3a,0) to the point x is |x−3a|.
- The distance from the charge −2q at (−3a,0) to the point x is |x+3a|.
- Therefore, the potential at point x is:
V(x)=q4πϵ0|x−3a|+−2q4πϵ0|x+3a|
- To find the points where the potential is zero, we set:
q|x−3a|=2q|x+3a|
- Simplifying this gives:
|x−3a|=2|x+3a|
- We will consider two cases based on the absolute values:
- Case 1: x−3a=2(x+3a)
x−3a=2x+6a⟹−x=9a⟹x=−9a
- Case 2: −(x−3a)=2(x+3a)
−x+3a=2x+6a⟹3a−6a=3x⟹−3a=3x⟹x=−a
- The potential will be positive near the positive charge q and negative near the negative charge −2q.
- The potential will approach infinity as we get close to the charges and will cross zero at the points found above.
- The graph of potential V versus position x will show:
- A steep rise towards positive infinity as x approaches 3a from the left.
- A drop to zero at x=−a.
- A steep drop to negative infinity as x approaches −3a from the right.
- The potential will also cross zero at x=−9a.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Matrix Matching
2 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced
44 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
Electric potential is a scalar quantity. Due to a point charge charge q at distance r, the potential is given by V=q4π∈0r. A point charge q is placed at (3a,0) and another charge −2q is placed at (−3a,0).
At how many points on the x-axis, (at finite distance) electric potential will be zero?
View SolutionA positive point charge q1 is placed at (a,0) and another positive point charge q2 is placed at (0,a) . Find the force acting on q1.
View Solution
Knowledge Check
Metallic sphere of radius R is charged to potential V. Then charge q is proportional to
AVBRCboth V and RDnone of these
Obtain an expression for electric potential .V due to a point charge .Q at a distance r.
View SolutionTwo point charges q each are fixed at (a,0) and (-a,0). A third charge Q is placed at origin. Electrons potential energy of the system will
View SolutionShow that electric potential at a point P, at a distance .r. from a fixed point charge Q, is given by :
V=(14πε0)Qr
View SolutionTwo equal charges q are placed at a distance of 2a and a third charge −2q is placed at the midpoint. The potential energy of the system is
View Solution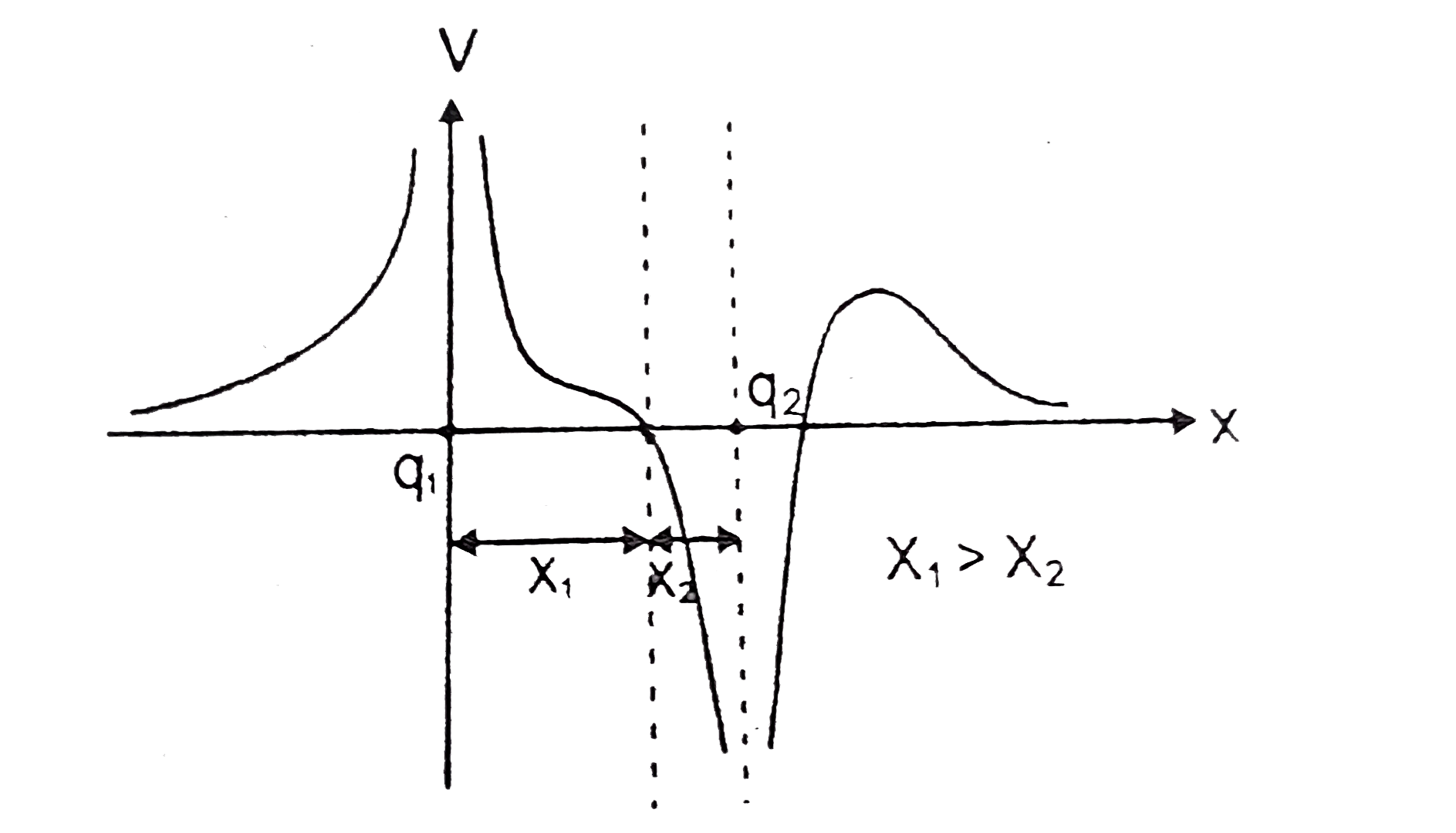
Two point charges (q1 and q2) are placed on x-axis, figure shows graph potential (V) on x-axis. With x-co-ordinate:
View SolutionTwo point charges (Q each are placed at (0,y) and (0-y) A point charge q of the same polarity can move along the x-axis. Then
View SolutionA point charge q is placed at a distance of r from cebtre of an uncharged conducting sphere of rad R(<r). The potential at any point on the sphere is
View Solution
