Infinite number of bodies, each of mass 2kg are situated on X-axis at distance 1m,2m,4m,8m, respectively from the origin, What is the resulting gravitational potential due to this system at the origin ?
To find the resulting gravitational potential at the origin due to an infinite number of bodies, each with a mass of 2 kg located at distances of 1 m, 2 m, 4 m, 8 m, and so on along the X-axis, we can follow these steps:
Step 1: Understand the formula for gravitational potential
The gravitational potential V at a point due to a mass m at a distance r is given by the formula:
V=−Gmr
where G is the gravitational constant.
Step 2: Identify the masses and distances
In this case, we have an infinite series of masses, each of mass m=2kg located at distances r=1m,2m,4m,8m,….
Step 3: Calculate the gravitational potential from each mass
The total gravitational potential at the origin due to all these masses can be expressed as:
V=−∞∑i=0G⋅2ri
where ri=2i for i=0,1,2,….
Step 4: Substitute the distances into the potential formula
Substituting the distances into the potential formula, we have:
V=−2G(11+12+14+18+…)
Step 5: Recognize the series
The series 11+12+14+18+… is a geometric series with the first term a=1 and common ratio r=12. The sum of an infinite geometric series is given by:
S=a1−r
Substituting the values, we get:
S=11−12=2
Step 6: Substitute the sum back into the potential formula
Now substituting the sum back into the potential formula:
V=−2G⋅2=−4G
Step 7: Final Result
Thus, the resulting gravitational potential at the origin due to this infinite system of masses is:
V=−4G
The gravitational potential V at a point due to a mass m at a distance r is given by the formula:
V=−Gmr
where G is the gravitational constant.
In this case, we have an infinite series of masses, each of mass m=2kg located at distances r=1m,2m,4m,8m,….
The total gravitational potential at the origin due to all these masses can be expressed as:
V=−∞∑i=0G⋅2ri
where ri=2i for i=0,1,2,….
Substituting the distances into the potential formula, we have:
V=−2G(11+12+14+18+…)
The series 11+12+14+18+… is a geometric series with the first term a=1 and common ratio r=12. The sum of an infinite geometric series is given by:
S=a1−r
Substituting the values, we get:
S=11−12=2
Now substituting the sum back into the potential formula:
V=−2G⋅2=−4G
Thus, the resulting gravitational potential at the origin due to this infinite system of masses is:
V=−4G
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Solved Examples16videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Examples8videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE10videos
KINEMATICS
Similar Questions
Infinite number of bodies, each of mass 2kg, are situated on x-axis at distance 1m,2m,4m,8m......... respectively, from the origin. The resulting gravitational potential due to this system at the origin will be
View SolutionInfinite number of bodies, each of mass 2kg, are situated on x-axis at distance 1m,2m,4m,8m......... respectively, from the origin. The resulting gravitational potential the to this system at the origing will be
View SolutionAn infinite number of particles each of mass m are placed on the positive X-axis of 1m,2m,4m,8m,... from the origin. Find the magnitude of the resultant gravitational force on mass m kept at the origin.
View SolutionInfinite number of masses, each of mass 3 kg are placed along the y-axis at y = 1 m, 3 m, 9 m 27 m ... The magnitude of resultant gravitational potential in terms of gravitatinal constant at the origin (y = 0) is
View SolutionInfinite number of masses, each of 1kg, are placed along the x-axis at x=±1m,±2m,±4m,±8m,±16m.. The gravitational of the resultant gravitational potential in term of gravitaitonal constant G at the origin (x=0) is
View SolutionAn infinite number of charges each q are placed in the x-axis at distances of 1, 2, 4, 8, ………meter from the origin. If the charges are alternately positive and negative find the intensity of electric field at origin.
View SolutionMasses of 1kg each are placed 1m,2m,4m,8m, ... from a point P. The gravitational field intensity at P due to these masses is
View SolutionConsider an infinite distribution of point masses (each of mass m) placed on x-axis as shown in the diagram. What is the gravitational force acting on the point mass placed at the origin ?
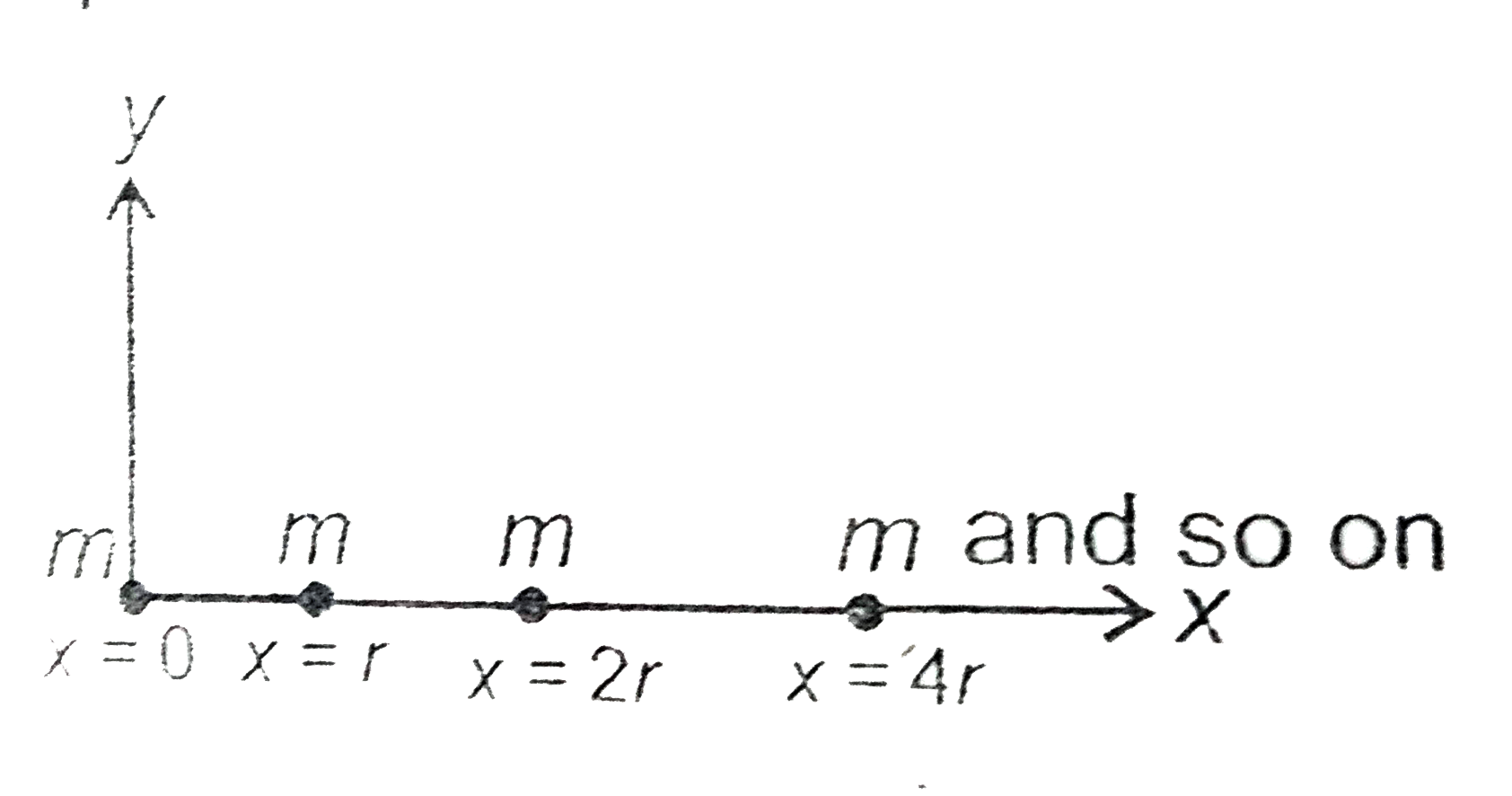 View Solution
View SolutionTwo bodies of masses m1 and m2 are placed distant d apart. Show that the position where the gravitational field due to them is zero, the potential is given by, V=−Gd(m1+m2+2√m1m2)
View SolutionTwo spheres each of mass 104 kg are separated by a distance of 100 m. What will be the gravitationel potential energy of the system?
View Solution

