Satellites in Circular Orbit
Step-by-Step Text Solution for Satellites in Circular Orbit:
1. Understanding Satellite Types:
- There are three main types of satellites: Geostationary, Geosynchronous, and Polar satellites.
- Geostationary Satellites: These satellites appear stationary relative to a point on Earth. They orbit the Earth with a period of 24 hours and are positioned directly above the equator.
- Geosynchronous Satellites: These satellites also have a 24-hour orbital period but can be at an angle to the equator, making them appear to move in a figure-eight pattern over the Earth.
- Polar Satellites: These satellites orbit the Earth in a path that passes over the poles, allowing them to cover the entire surface of the Earth over time.
2. Orbital Radius:
- The radius of the orbit varies among the types of satellites:
- Geostationary satellites have the largest orbital radius.
- Geosynchronous satellites have a smaller radius than geostationary satellites.
- Polar satellites have the smallest orbital radius.
3. Orbital Velocity:
- The orbital velocity (v) of a satellite in circular orbit can be derived from the gravitational force acting on it.
- The formula for the orbital velocity is given by:
v=√GMr
where:
- G is the gravitational constant (6.674×10−11m3/kg⋅s2),
- M is the mass of the Earth (approximately 5.972×1024kg),
- r is the radius of the orbit (distance from the center of the Earth to the satellite).
4. Application of the Formula:
- To find the orbital velocity of a satellite, you need to know the radius of its orbit. For example, if a satellite is in a geostationary orbit, its radius can be calculated using the formula for gravitational force and centripetal force balance.
5. Conclusion:
- Understanding the types of satellites and their respective orbits is crucial for applications in communication, weather monitoring, and Earth observation.
---
- There are three main types of satellites: Geostationary, Geosynchronous, and Polar satellites.
- Geostationary Satellites: These satellites appear stationary relative to a point on Earth. They orbit the Earth with a period of 24 hours and are positioned directly above the equator.
- Geosynchronous Satellites: These satellites also have a 24-hour orbital period but can be at an angle to the equator, making them appear to move in a figure-eight pattern over the Earth.
- Polar Satellites: These satellites orbit the Earth in a path that passes over the poles, allowing them to cover the entire surface of the Earth over time.
- The radius of the orbit varies among the types of satellites:
- Geostationary satellites have the largest orbital radius.
- Geosynchronous satellites have a smaller radius than geostationary satellites.
- Polar satellites have the smallest orbital radius.
- The orbital velocity (v) of a satellite in circular orbit can be derived from the gravitational force acting on it.
- The formula for the orbital velocity is given by:
v=√GMr
where:
- G is the gravitational constant (6.674×10−11m3/kg⋅s2),
- M is the mass of the Earth (approximately 5.972×1024kg),
- r is the radius of the orbit (distance from the center of the Earth to the satellite).
- To find the orbital velocity of a satellite, you need to know the radius of its orbit. For example, if a satellite is in a geostationary orbit, its radius can be calculated using the formula for gravitational force and centripetal force balance.
- Understanding the types of satellites and their respective orbits is crucial for applications in communication, weather monitoring, and Earth observation.
Similar Questions
Consider earth satellites in circular orbits. A geostationary satellite must be at a height of about 36000 km from the earth's surface. Will any satellite moving at this height be a geostationary satellite? Will any satellite moving at this height have a time period of 24 hours?
View SolutionEnergy of a satellite in circular orbit is E0. The energy required to move the satellite to a circular orbit of 3 times the radius of the initial orbit is
View Solution
Knowledge Check
The period of a satellite in a circular orbit of radius R is T. What is the period of another satellite in a circular orbit of radius 4 R ?
A4 TBT/8CT/4D8 TMatch the Column I with Column II
For a satellite in circular orbit
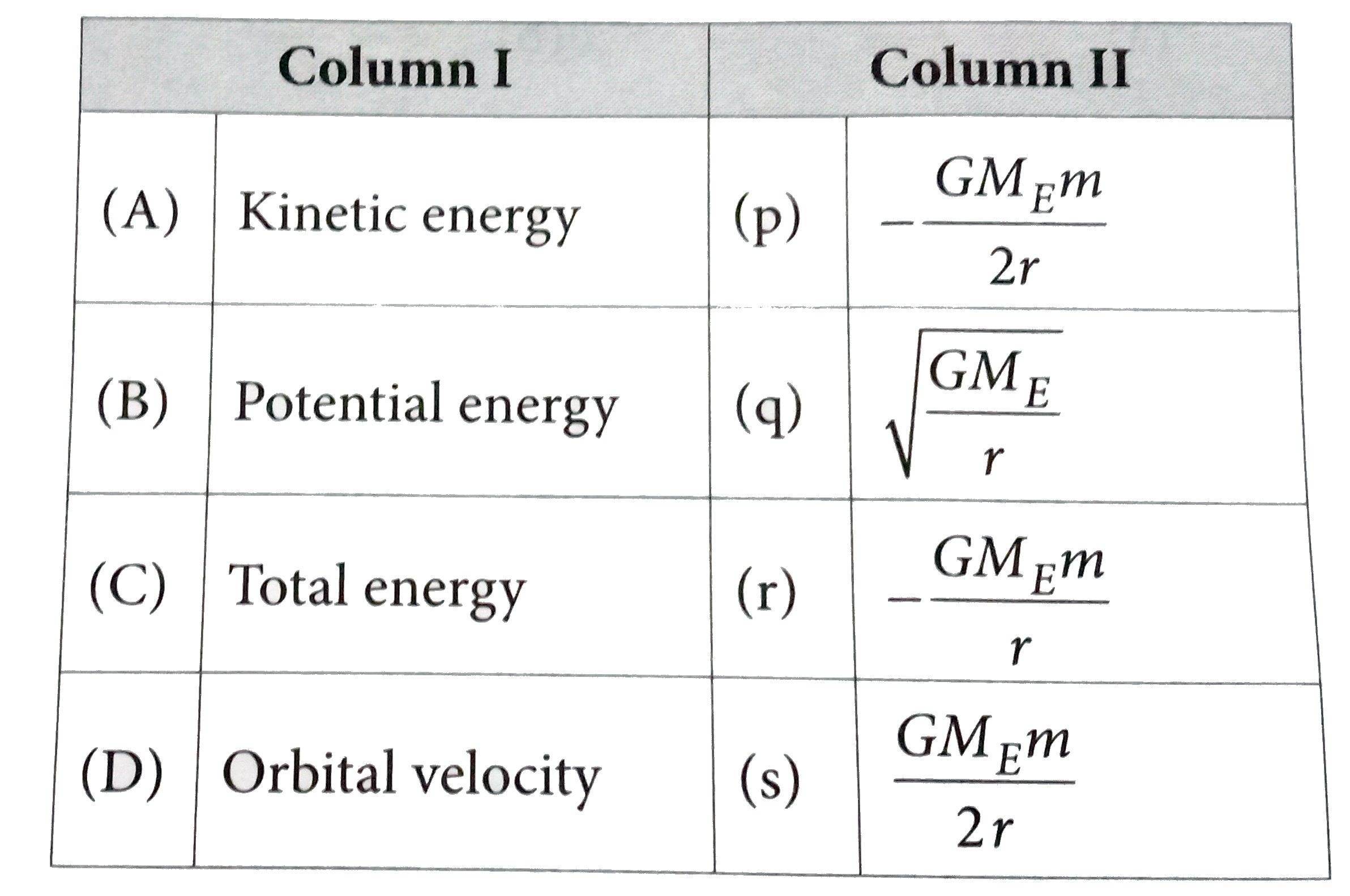
(where ME is the mass of the earth , m is the mass of the satellite and r is the radius of the orbit )AA-r, B-s,C-q,D-pBA-q,B-p,C-r,D-sCA-p,B-q,C-s,D-rDA-s,B-r,C-p,D-qThe time period of an artificial satellite in a circular orbit of radius R is 2 days and its orbital velocity is v0. If time period of another satellite in a circular orbit is 16 days then
Aits radius of orbit is 4R and orbital velocity is v0Bits radius of orbit is 4R and orbital velocity is v02Cits radius of orbit is 2R and orbital velocity is v0Dits radius of orbit is 2R and orbital velocity is v02
Energy of a satellite in circular orbit is E0. The energy required to move the satellite to a circular orbit of 3 time the radius of the initial orbit is x3E0. Find the value of x.
View SolutionThe time period of a satellite in a circular orbit around the earth is T . The kinetic energy of the satellite is proportional to T−n . Then, n is equal to :
View SolutionMatch the following columns
Column-IColumn-II(A)Time period of an earthsatellite in circular orbit(p)Independent of mass of satellite(B)Orbital velocity of satellite(q)Independent of radius of orbit(C)Mechanical energy of satellite(r)Independent of mass of earth(s)None
View SolutionWhen a satellite in a circular orbit around the earth enters the atmospheric region, it encounters small air resistance to its motion. Then
View SolutionWhen a satellite in a circular orbit around the earth enters the atmospheric region, it encounters small air resistance to its motion. Then
View Solution
