A proton is fixed at origin. Another proton is released from rest, from a point at a distance r from origin. Taking charge of portion as e and mass as m, find the speed of the proton (i) at a distance 2r from origin (ii) at large distance from origin.
To solve the problem, we will use the principle of conservation of energy. The total mechanical energy (kinetic energy + potential energy) of the system remains constant if only conservative forces are acting on it.
Given:
- Charge of proton, q=e
- Mass of proton, m
- Initial distance from origin, r
- Final distances to consider: 2r and infinity
Step 1: Calculate the speed of the proton at distance 2r
1. Initial Energy Calculation:
- The initial potential energy Ui when the proton is at distance r:
Ui=−k⋅e⋅er=−ke2r
- The initial kinetic energy Ki is zero since the proton is released from rest:
Ki=0
2. Final Energy Calculation at distance 2r:
- The final potential energy Uf when the proton is at distance 2r:
Uf=−k⋅e⋅e2r=−ke22r
- Let the final kinetic energy Kf be:
Kf=12mv2
3. Applying Conservation of Energy:
Ki+Ui=Kf+Uf
Substituting the values:
0−ke2r=12mv2−ke22r
4. Rearranging the equation:
−ke2r+ke22r=12mv2
−2ke22r+ke22r=12mv2
−ke22r=12mv2
5. Solving for v2:
v2=ke2r⇒v=√ke2r
Step 2: Calculate the speed of the proton at large distance (infinity)
1. Initial Energy Calculation (same as before):
Ui=−ke2r,Ki=0
2. Final Energy Calculation at infinity:
- The potential energy Uf at infinity is zero:
Uf=0
- Let the final kinetic energy Kf be:
Kf=12mv2
3. Applying Conservation of Energy:
Ki+Ui=Kf+Uf
Substituting the values:
0−ke2r=12mv2+0
4. Rearranging the equation:
−ke2r=12mv2
5. Solving for v2:
v2=2ke2m⇒v=√2ke2m
Final Answers:
- Speed of the proton at distance 2r:
v=√ke2r
- Speed of the proton at large distance (infinity):
v=√2ke2m
- Charge of proton, q=e
- Mass of proton, m
- Initial distance from origin, r
- Final distances to consider: 2r and infinity
- The initial potential energy Ui when the proton is at distance r:
Ui=−k⋅e⋅er=−ke2r
- The initial kinetic energy Ki is zero since the proton is released from rest:
Ki=0
- The final potential energy Uf when the proton is at distance 2r:
Uf=−k⋅e⋅e2r=−ke22r
- Let the final kinetic energy Kf be:
Kf=12mv2
Ki+Ui=Kf+Uf
Substituting the values:
0−ke2r=12mv2−ke22r
−ke2r+ke22r=12mv2
−2ke22r+ke22r=12mv2
−ke22r=12mv2
v2=ke2r⇒v=√ke2r
Ui=−ke2r,Ki=0
- The potential energy Uf at infinity is zero:
Uf=0
- Let the final kinetic energy Kf be:
Kf=12mv2
Ki+Ui=Kf+Uf
Substituting the values:
0−ke2r=12mv2+0
−ke2r=12mv2
v2=2ke2m⇒v=√2ke2m
- Speed of the proton at distance 2r:
v=√ke2r
- Speed of the proton at large distance (infinity):
v=√2ke2m
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.1
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.2
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
When E⊥B and the particle is released at rest from origin.
View SolutionFind the distance from the origin to each of the point:
(4,−1,2)
View SolutionFind the distance from the origin to each of the point:
(2,2,3)
View SolutionFind the distance from the origin to (6,6,7).
View SolutionFind the distance from the origin to each of the point:
(0,4,−4)
View SolutionFind the locus of point whose distance from the origin is 5.
View Solution4 charges are placed each at a distance a from origin . The dipole moment of configuration is .
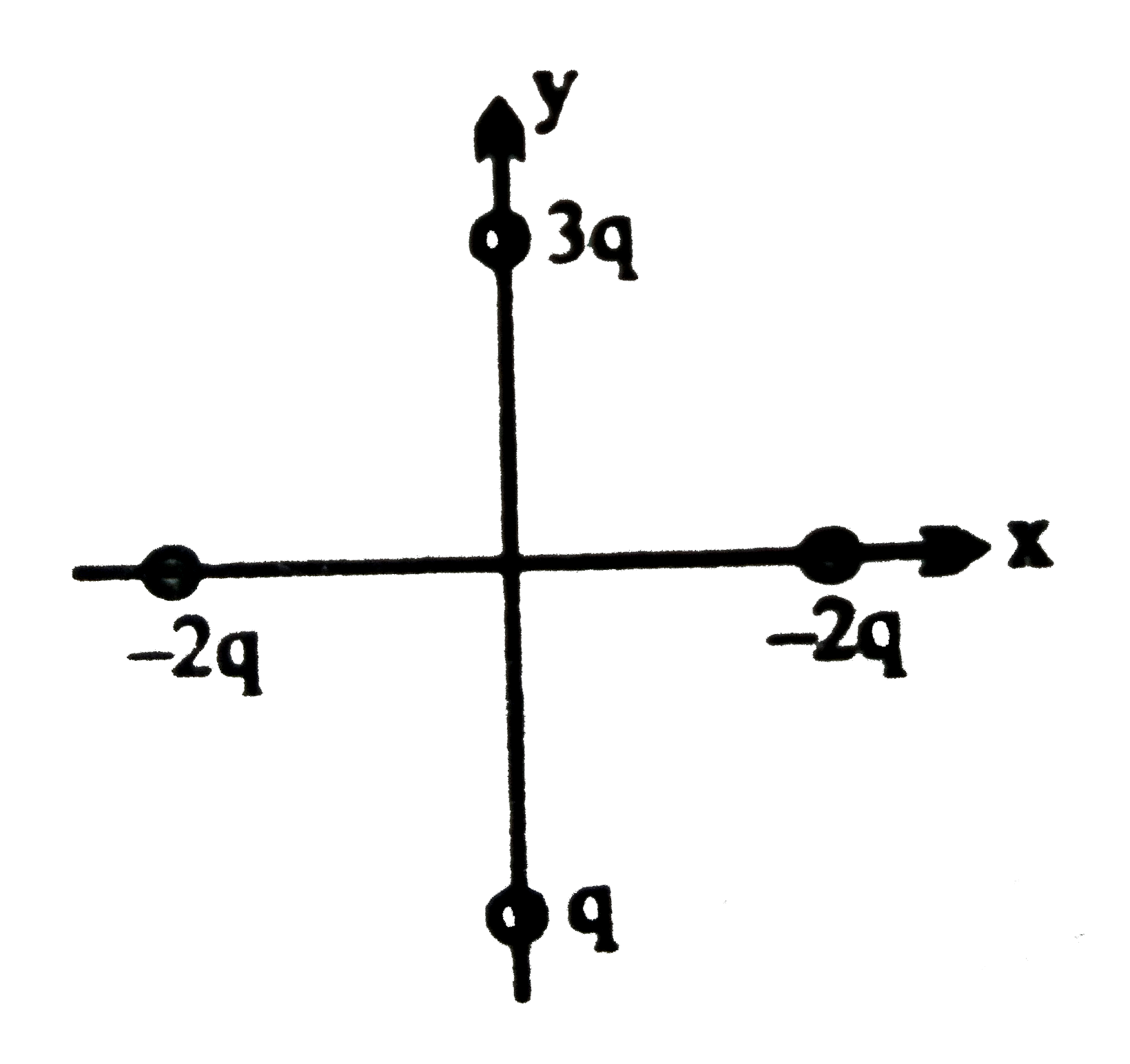 .
.
View SolutionAll the particles of a body situated at distance R from the origin. The distance of the center of mass of the body from the origin is
View SolutionFind the distance from the origin to each of the point:
(−4,−3,−2)
View SolutionA positive charge is released from rest at a distance r0 from a positive line charge with uniform density . The speed (v) of the point charge , as a function of instantaneous distance r from line charge, is proportional to:
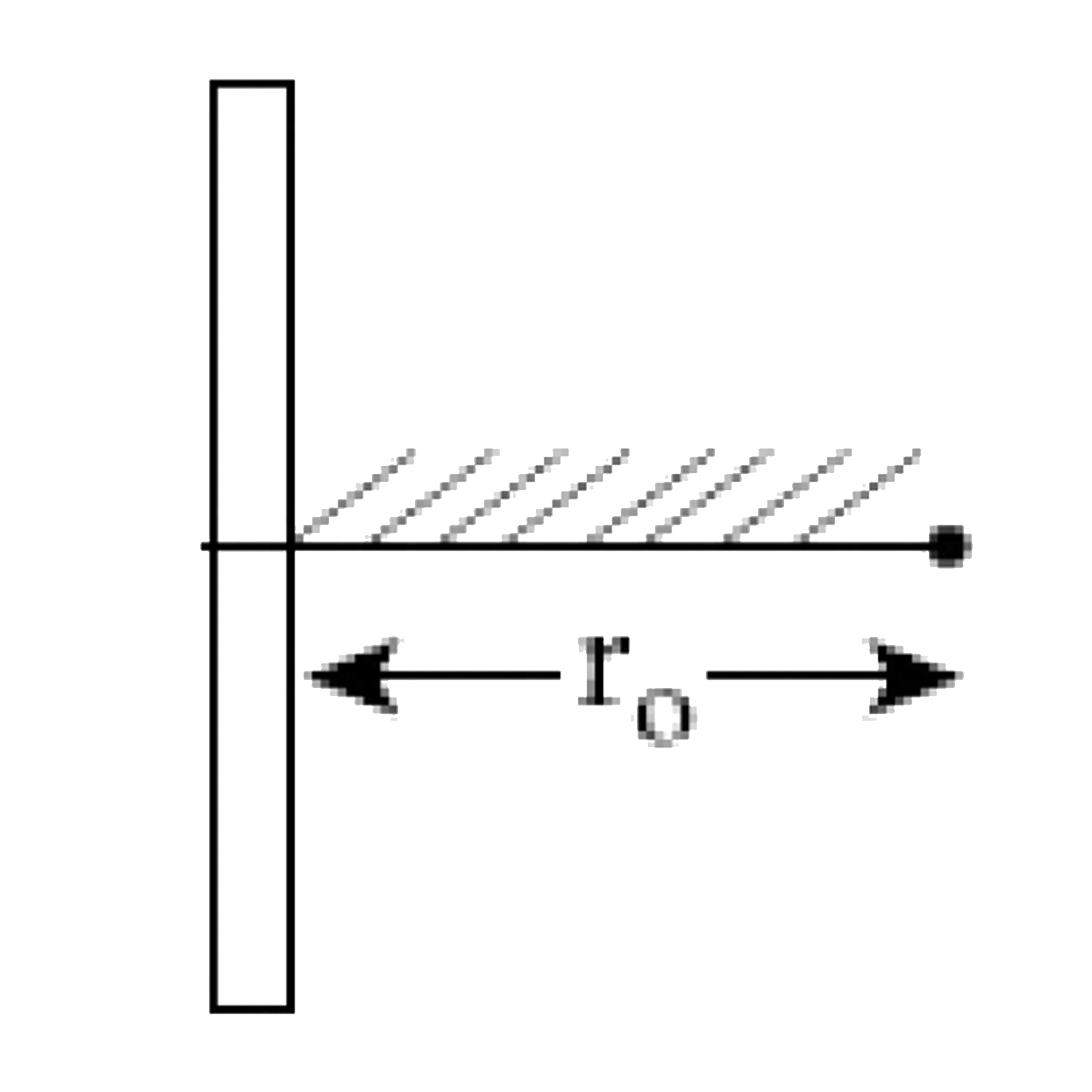
View Solution
