An isolated 16μF parallel plate air capacitor has a potential difference of 100 V. dielectric slab having relative permittivity (i.e., dielectric constant) = 5 is introduced to fill the space between the two plates completely. Calculate.
(i) the new capacitance of the capacitor
(ii) the new potential differece between the two plates of capacitor.
To solve the problem step by step, we will calculate the new capacitance of the capacitor after introducing the dielectric slab and then determine the new potential difference across the capacitor plates.
Step 1: Calculate the new capacitance
The capacitance of a capacitor with a dielectric material can be calculated using the formula:
C′=K⋅C
Where:
- C′ is the new capacitance,
- K is the dielectric constant (relative permittivity),
- C is the original capacitance.
Given:
- The original capacitance C=16μF=16×10−6F,
- The dielectric constant K=5.
Substituting the values into the formula:
C′=5⋅(16×10−6)=80×10−6F
Thus, the new capacitance C′ is:
C′=80μF
Step 2: Calculate the initial charge on the capacitor
The charge Q on a capacitor can be calculated using the formula:
Q=C⋅V
Where:
- Q is the charge,
- C is the capacitance,
- V is the potential difference.
Given:
- The original potential difference V=100V.
Substituting the values:
Q=(16×10−6)⋅100=1.6×10−4C
Step 3: Calculate the new potential difference
Since the capacitor is isolated, the charge remains constant when the dielectric is introduced. The new potential difference V′ can be calculated using the formula:
V′=QC′
Substituting the values of Q and C′:
V′=1.6×10−480×10−6=20V
Final Answers
(i) The new capacitance of the capacitor is 80μF.
(ii) The new potential difference between the two plates of the capacitor is 20V.
---
The capacitance of a capacitor with a dielectric material can be calculated using the formula:
- C′ is the new capacitance,
- K is the dielectric constant (relative permittivity),
- C is the original capacitance.
- The original capacitance C=16μF=16×10−6F,
- The dielectric constant K=5.
The charge Q on a capacitor can be calculated using the formula:
- Q is the charge,
- C is the capacitance,
- V is the potential difference.
- The original potential difference V=100V.
Since the capacitor is isolated, the charge remains constant when the dielectric is introduced. The new potential difference V′ can be calculated using the formula:
(i) The new capacitance of the capacitor is 80μF.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.1
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.2
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
A dielectric slab of relative premittivity (i.e. dielectric constant) 6 is introduced between the two plates of an 8μF air capacitor, in order to completely occupy the space between the two plates. Find the new capacitance of the capacitor.
View SolutionA parallel plate capacitor is charged by a battery, which is then disconnected. A dielectric slab is now introduced between the two plates to occupy the space completely. State the effect on the following:
(i) the capacitance of the capacitor.
(ii) potential difference between the plates.
(iii) the energy stored in the capacitor.
View Solution
Knowledge Check
A parallel plate air capacitor has a capacitance C. When it is half filled with a dielectric of dielectric constant 5, the percentage increase in the capacitance will be
A400%B66.6%C33.3%D200%
In a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
_2019_CBT2_E01_002_Q01.png)
View SolutionA paller- plate capacitor has plate area 100cm2 and plate separation 1.0cm.A glass plate (dielectric constant 4.0)are inserted one over the other the fill the space between the plate of the capacitor.Find the new capacitance.
View SolutionIf a thin metal foil of same area is placed between the two plates of a parallel plate capacitor of capacitance C, then new capacitance will be
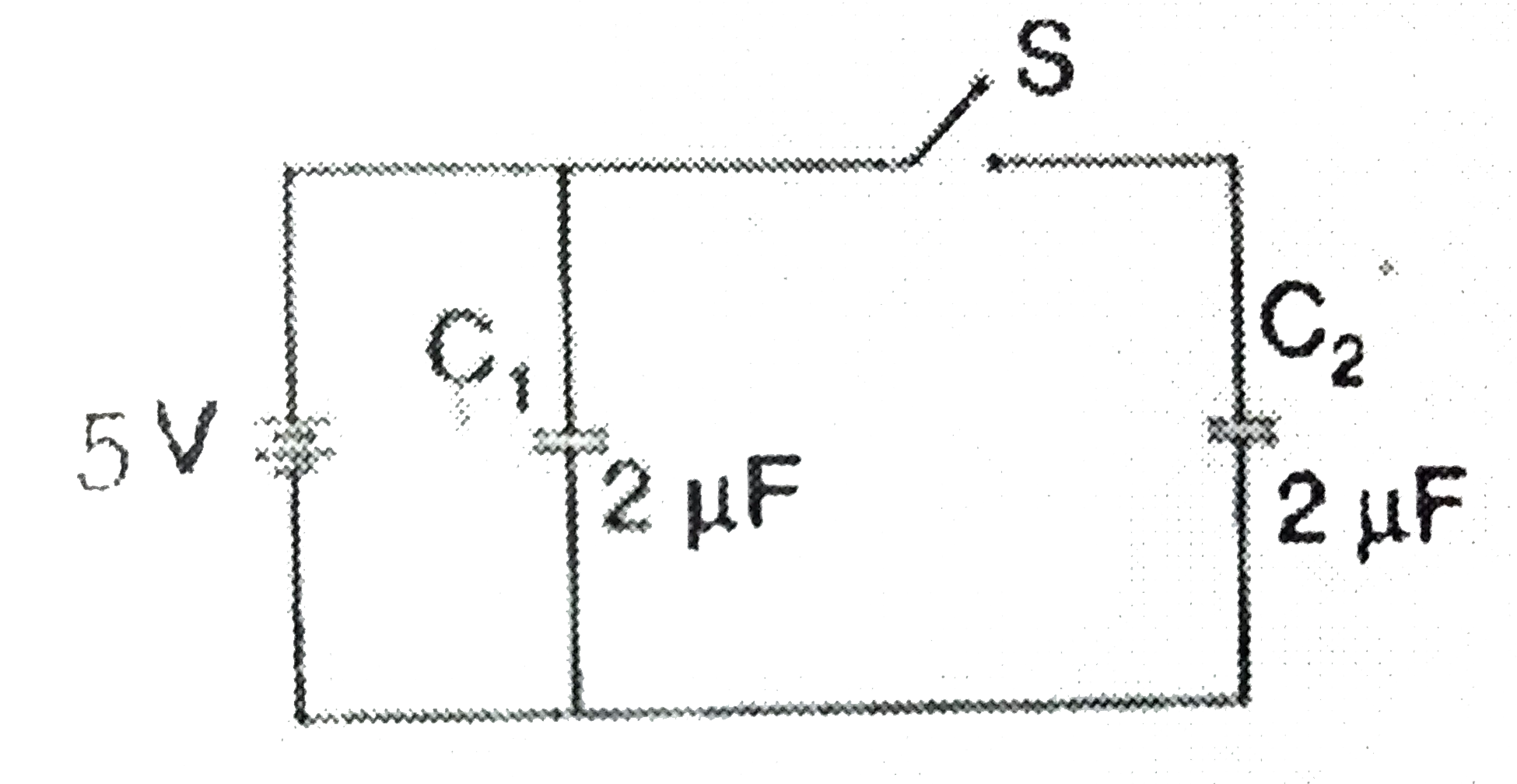
View SolutionFigure shows two identical capacitors C1andC2 each of 2μF capacitance, connected to a battery of 5 V. Initially switch 'S' is closed. After some time 'S' is left open and dielectric slavs of dielectric constant K = 5 are inserted to fill completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted?
View SolutionThe plates of a parallel plate capacitor with no dielectirc are connected to a volatage source. Now a dielectric of dielectric constant K is inserted to fill the whose space between the plates with voltage source remainign connected to the capacitor-
View SolutionA parallel plate capacitor is charged by a battery. After sometime the battery is disconnected and a dielectric slab with its thickness equal to the plate separation is inserted between the plates. How will (i) the capacitance of the capacitor, (ii) potential difference between the plates and (iii) the energy stored in the capacitor be affected ?
Justify your answer in each case.
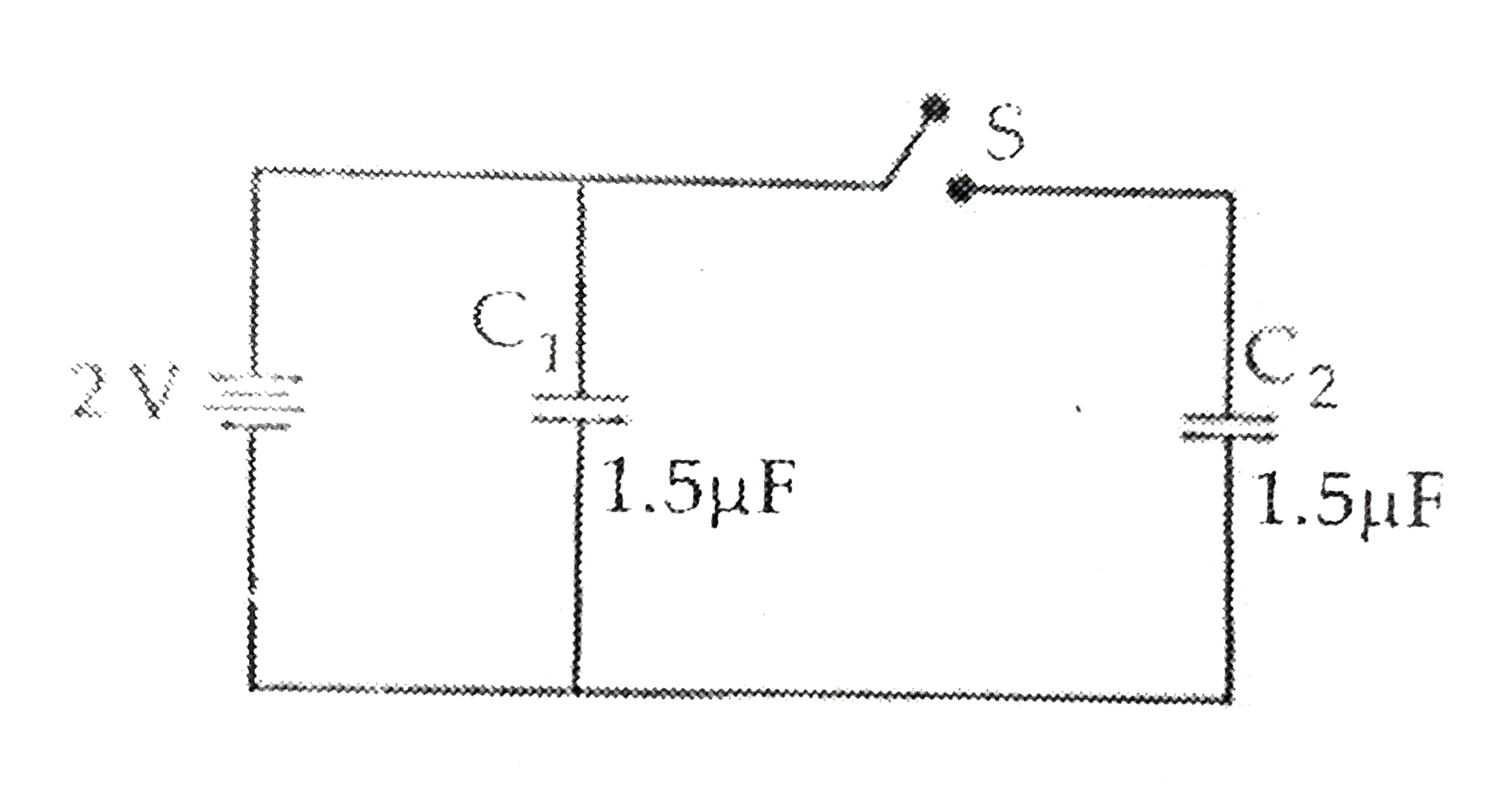
View SolutionFigure shows two identical caoacitors C1andC2 each of 1.5μF caoacitance, connected to a battery of 2 V. Initially switch 'S' is closed. After some time 's' is left open and dielectric slabs of dielectric constant K=2 are inserted to fill completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted.
View Solution
