A letter A consists of a uniform wire of resistance 1 ohm per cm. The sides of the letter are each 20 cm long and the cross-piece in the middle is 10 cm long while the apex angle is . Find the resistance of the letter between the two ends of the legs.
To solve the problem, we need to find the resistance of the letter "A" formed by a uniform wire with a resistance of 1 ohm per cm. The letter consists of two legs and a crosspiece. Here’s how we can approach the solution step-by-step:
Step 1: Understand the Structure of the Letter A
The letter "A" consists of:
- Two legs, each 20 cm long.
- A crosspiece in the middle that is 10 cm long.
- The apex angle is 60 degrees.
Step 2: Calculate the Resistance of Each Segment
The resistance per cm of the wire is given as 1 ohm. Therefore, we can calculate the resistance of each segment:
- Legs: Each leg is 20 cm long, so the resistance of each leg (R_leg) is:
Rleg=20cm×1ohm/cm=20ohms
- Crosspiece: The crosspiece is 10 cm long, so the resistance of the crosspiece (R_cross) is:
Rcross=10cm×1ohm/cm=10ohms
Step 3: Identify Series and Parallel Connections
- The two legs are in series with each other.
- The crosspiece is in parallel with the combination of the two legs.
Step 4: Calculate the Total Resistance of the Legs
Since both legs are in series, the total resistance of the legs (R_series) is:
Rseries=Rleg+Rleg=20ohms+20ohms=40ohms
Step 5: Calculate the Equivalent Resistance of the Parallel Connection
Now, we need to find the equivalent resistance of the series combination of the legs and the crosspiece which are in parallel:
1Req=1Rseries+1Rcross
Substituting the values:
1Req=140ohms+110ohms
Finding a common denominator (40):
1Req=140+440=540=18
Thus, the equivalent resistance (R_eq) is:
Req=8ohms
Final Answer
The resistance of the letter "A" between the two ends of the legs is 8 ohms.
---
The letter "A" consists of:
- Two legs, each 20 cm long.
- A crosspiece in the middle that is 10 cm long.
- The apex angle is 60 degrees.
The resistance per cm of the wire is given as 1 ohm. Therefore, we can calculate the resistance of each segment:
- Legs: Each leg is 20 cm long, so the resistance of each leg (R_leg) is:
Rleg=20cm×1ohm/cm=20ohms
- Crosspiece: The crosspiece is 10 cm long, so the resistance of the crosspiece (R_cross) is:
Rcross=10cm×1ohm/cm=10ohms
- The two legs are in series with each other.
- The crosspiece is in parallel with the combination of the two legs.
Since both legs are in series, the total resistance of the legs (R_series) is:
Rseries=Rleg+Rleg=20ohms+20ohms=40ohms
Now, we need to find the equivalent resistance of the series combination of the legs and the crosspiece which are in parallel:
1Req=1Rseries+1Rcross
Substituting the values:
1Req=140ohms+110ohms
Finding a common denominator (40):
1Req=140+440=540=18
Thus, the equivalent resistance (R_eq) is:
Req=8ohms
The resistance of the letter "A" between the two ends of the legs is 8 ohms.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Taking it together
142 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Subjective
13 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
A piece of wire 20 cm long is bent into the form of an arc of a circle, subtending an angle of 60∘ at its centre. Find the radius of the circle.
View SolutionA wire of resistance 3 ohm and length 10 cm is stretched to length 30 cm. Assuming that it has a uniform cross section, what will be its new resistance ?
View SolutionA particular resistance wire has a resistance of 3.0 ohm per metre. Find :
The total resistance of three lengths of this wire each 1.5 m long, joined in parallel.
View SolutionA L cm long wire is bent to form a triangle with one of it's angle as 60∘.Find the sides of the triangle for which area is largest.
View SolutionTwo adjacent sides of a parallelogram are 28 cm and 26 cm. If one diagonal of it is 30 cm long, Find the area of the parallelogram. Also, find the distance between shorter sides.
View SolutionIn a rhombus ABCD, length of each side is 10 cm and ∠A=60∘. Find the lengths of its diagonals AC and BD.
View SolutionFind the magnitude of magetic moment of the current carrying lop ABCDEFA. Each side of the loop is 10cm long and current in the loop is i=2.0A
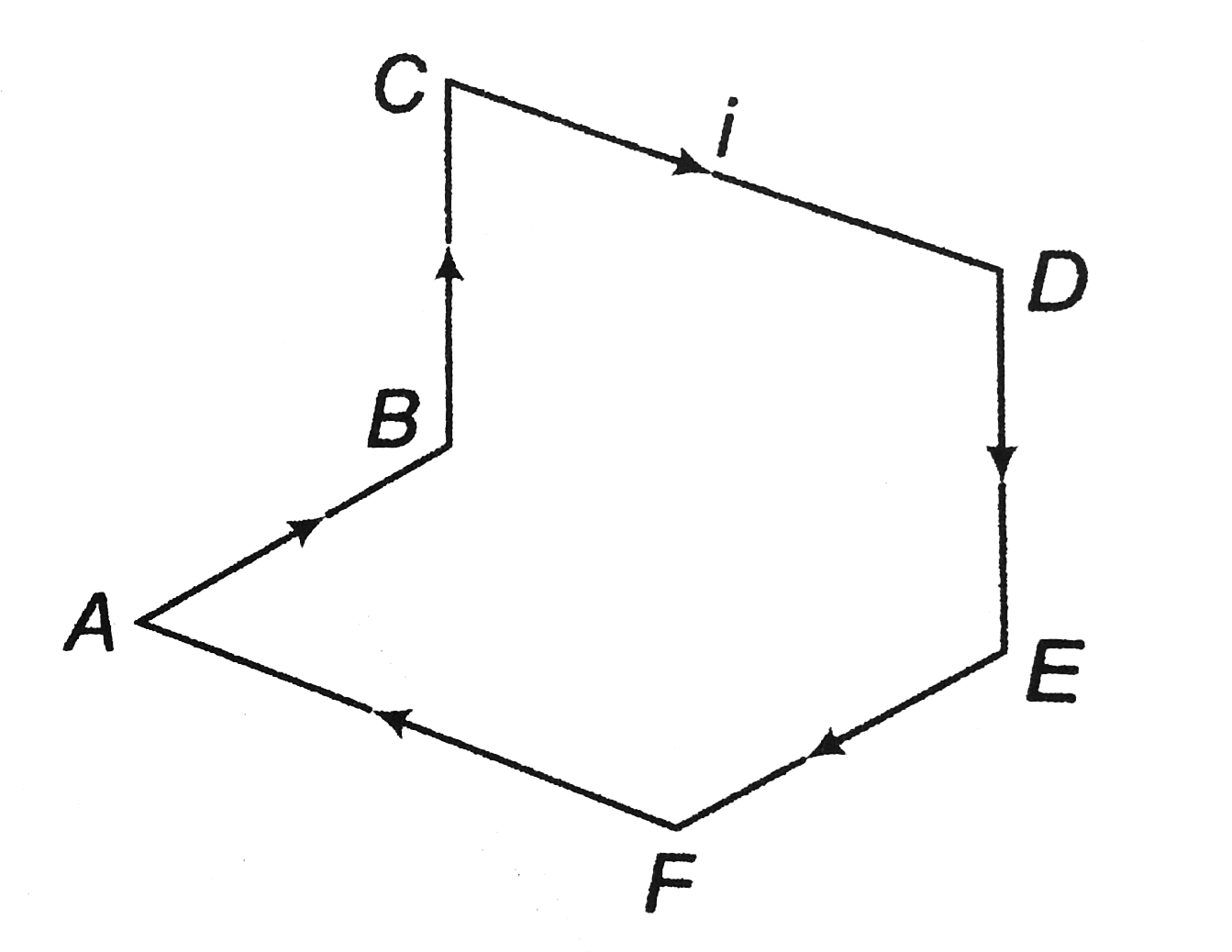
View SolutionFind the magnitude of magetic moment of the current carrying lop ABCDEFA. Each side of the loop is 10cm long and current in the loop is i=2.0A

View SolutionTwo adjacent sides of a parallelogram are 10 cm and 12 cm. If its one diagonal is 14 cm long, find the area of the parallelogram.
View SolutionA picture is painted on a cardboard 8 cm long and 5 cm wide such that there is a margin of 1.5 cm along each of its sides. Find the total area of the margin.
View Solution
