Two uniform wires A and B are of the same total metal and have equal masses. The radius of wire A is twice that of wire B. The total resistance of A and B when connected in parallel is
4Ω when the resistance of wire A is 4.25Ω
5Ω when the resistnace of wire A is 4Ω
4Ω when the resistance of wire B is 4.25Ω
5Ω when the resistance of wire B is 4Ω
The correct Answer is:A
To solve the problem, we need to find the total resistance of two uniform wires A and B connected in parallel. Given that both wires have the same mass and are made of the same material, we can derive their resistances based on their dimensions.
Step 1: Understand the relationship between radius and resistance
The resistance R of a wire is given by the formula:
R=ρLA
where:
- ρ is the resistivity of the material,
- L is the length of the wire,
- A is the cross-sectional area of the wire.
The cross-sectional area A of a wire with radius r is:
A=πr2
Step 2: Define the variables for wires A and B
Let:
- The radius of wire B be rB.
- The radius of wire A be rA=2rB (since the radius of wire A is twice that of wire B).
Step 3: Express the volumes of the wires
Since both wires have the same mass and are made of the same material, we can express their volumes in terms of their dimensions:
Volume=A⋅L
For wire A:
VA=π(r2A)LA=π(2rB)2LA=4πr2BLA
For wire B:
VB=π(r2B)LB
Since the masses are equal and the density is the same, we have:
ρVA=ρVB⟹VA=VB
Thus:
4πr2BLA=πr2BLB
Cancelling πr2B (assuming rB≠0) gives:
4LA=LB⟹LB=4LA
Step 4: Calculate the resistances of wires A and B
Now we can express the resistances of both wires using their lengths:
For wire A:
RA=ρLAπ(2rB)2=ρLA4πr2B
For wire B:
RB=ρLBπr2B=ρ(4LA)πr2B=4ρLAπr2B
Step 5: Relate the resistances
Now we can find the ratio of the resistances:
RBRA=4ρLAπr2BρLA4πr2B=414=16
Thus, we can say:
RB=16RA
Step 6: Calculate the equivalent resistance in parallel
The equivalent resistance Rp of two resistances RA and RB in parallel is given by:
1Rp=1RA+1RB
Substituting RB=16RA:
1Rp=1RA+116RA=16+116RA=1716RA
Thus:
Rp=16RA17
Step 7: Conclusion
The total resistance of wires A and B when connected in parallel is:
Rp=1617RA
The resistance R of a wire is given by the formula:
- ρ is the resistivity of the material,
- L is the length of the wire,
- A is the cross-sectional area of the wire.
Let:
- The radius of wire B be rB.
- The radius of wire A be rA=2rB (since the radius of wire A is twice that of wire B).
Since both wires have the same mass and are made of the same material, we can express their volumes in terms of their dimensions:
Now we can express the resistances of both wires using their lengths:
Now we can find the ratio of the resistances:
The equivalent resistance Rp of two resistances RA and RB in parallel is given by:
The total resistance of wires A and B when connected in parallel is:
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Two wires A and B have equal lengths and aremade of the same material , but diameter of wire A is twice that of wire B. Then, for a given load,
View SolutionTwo wires A and B have the same cross section and are made of the same material, but the length of wire A is twice that of B. Then, for a given load
View SolutionTwo wires A and B of equal masses and of the same material are taken. The diameter of wire A is half the diameter of wire B. if the resistance of wire A is 24Ω, calculate the resistance of wire B.
View SolutionThe following diagram represents an electrical circui containing two uniform resistance wires A and B connected to a single ideal cell. Both wires have same length, but thickness of wire B is twice that of wire A. The conducting wires connecting A and B to the ideal cell are resistanceless. The dependence of electric potential on position along the length of two wires is given in option.
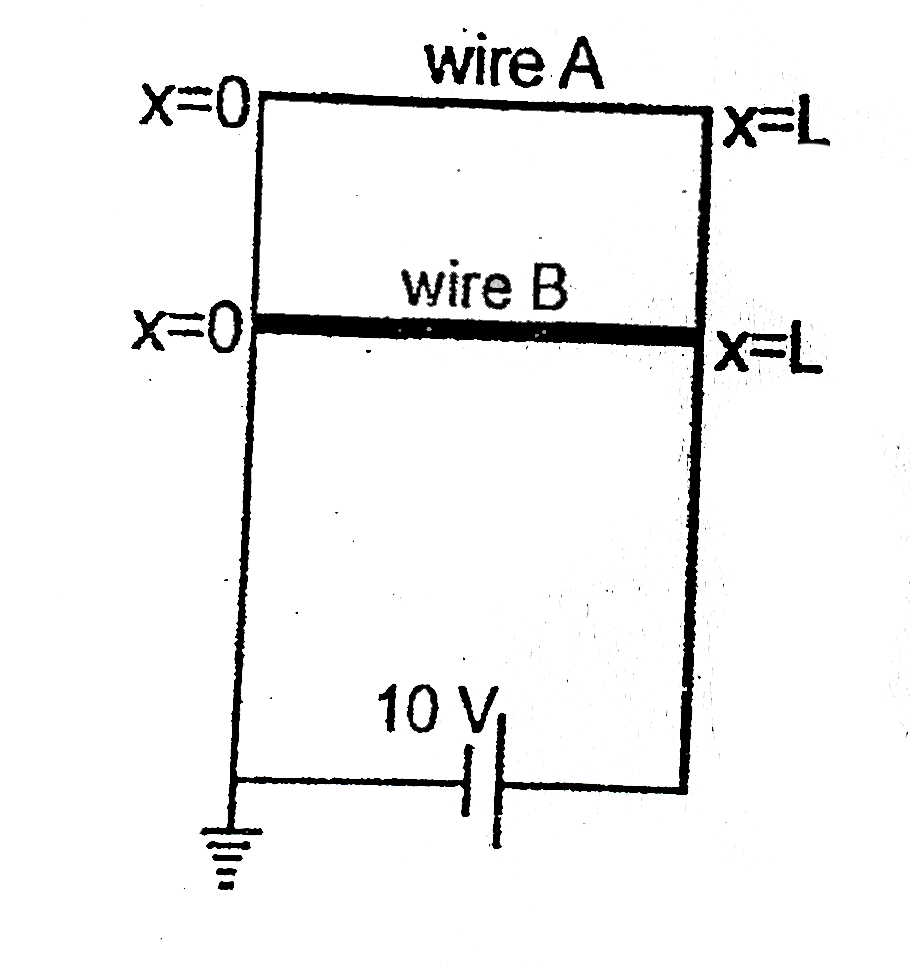
View SolutionTwo wires of the same materical having equal area of cross-section have L and 2L. Their respective resistances are in the ratio
View SolutionTwo wires A and B have the same length and area of cross-secton. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
View SolutionTwo wires 'A' and 'B' of the same material have their lengths in the ratio 1:2 and radii in the ratio 2:1 The two wires are connected in parallel across a battery. The ratio of the heat produced in 'A' to the heat produced in 'B' for the same time is
View SolutionTwo wires A and B of same dimensions are stretched by same amount of force .Young's modulus of A is twice that of B. Which wire will get more elongation?
View SolutionWires A and B have have identical lengths and have circular cross-sections. The radius of A is twice the radius of B i.e. RA=2RB. For a given temperature difference between the two ends, both wires conduct heat at the same rate. The relation between the thermal conductivities is given by-
View SolutionIf two conducting wires Aand B of same dimensions have electron density ratio 1: 3 . If their relaxation time is same then the ratio of resistance of A to resistance of B is
View Solution
