Out of five resistance of RΩ each 3 are connected in parallel and are joined to the rest 2 in series. Find the resultant resistance.
(3/7)RΩ
(7/3)RΩ
(7/8)RΩ
(8/7)RΩ
The correct Answer is:B
To find the resultant resistance of the given circuit, we will follow these steps:
Step 1: Identify the Configuration
We have 5 resistors, each of resistance RΩ. Out of these, 3 resistors are connected in parallel, and the remaining 2 resistors are connected in series with the parallel combination.
Step 2: Calculate the Equivalent Resistance of the Parallel Resistors
For resistors in parallel, the formula for equivalent resistance Rp is given by:
1Rp=1R1+1R2+1R3
Since all three resistors have the same resistance R:
1Rp=1R+1R+1R=3R
Thus, the equivalent resistance Rp is:
Rp=R3
Step 3: Calculate the Equivalent Resistance of the Series Resistors
The two resistors connected in series will have an equivalent resistance Rs given by:
Rs=R+R=2R
Step 4: Combine the Results
Now, we combine the equivalent resistance of the parallel resistors Rp with the equivalent resistance of the series resistors Rs:
Req=Rp+Rs=R3+2R
To add these, we need a common denominator:
Req=R3+6R3=7R3
Final Result
The resultant resistance of the entire circuit is:
Req=7R3Ω
We have 5 resistors, each of resistance RΩ. Out of these, 3 resistors are connected in parallel, and the remaining 2 resistors are connected in series with the parallel combination.
For resistors in parallel, the formula for equivalent resistance Rp is given by:
1Rp=1R1+1R2+1R3
Since all three resistors have the same resistance R:
1Rp=1R+1R+1R=3R
Thus, the equivalent resistance Rp is:
Rp=R3
The two resistors connected in series will have an equivalent resistance Rs given by:
Rs=R+R=2R
Now, we combine the equivalent resistance of the parallel resistors Rp with the equivalent resistance of the series resistors Rs:
Req=Rp+Rs=R3+2R
To add these, we need a common denominator:
Req=R3+6R3=7R3
The resultant resistance of the entire circuit is:
Req=7R3Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:B. Assertion and reason
Explore 18 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Match the columns
Explore 4 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Check point
Explore 70 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Subjective
Explore 11 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Medical entrances gallery
Explore 25 Videos
Similar Questions
Four resistors each of resistance 2 Ω are connected in parallel. What is the effective resistance ?
View SolutionA set of n identical resistors, each of resistance RΩ, when connected in series have an effective resistance XΩ and when the resistors are connected in parallel, their effective resistance is YΩ. Find the relation between R, X and Y.
View Solution
Knowledge Check
Five equal resistances of 10Ω are connected between A and B as shown in figure. The resultant resistance
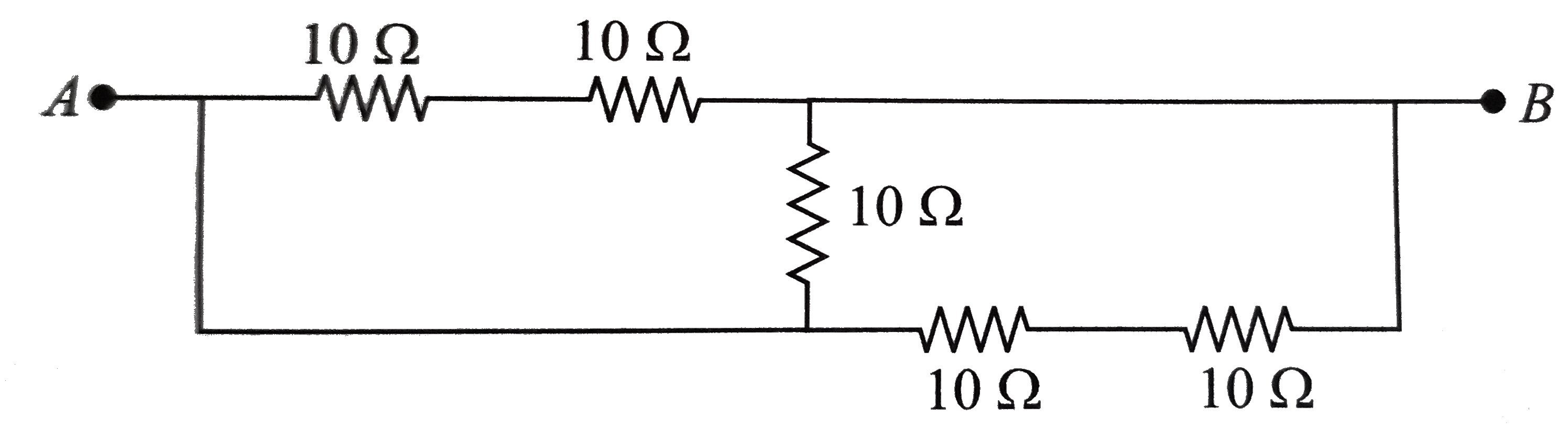 A10ΩB5ΩC15ΩD6Ω
A10ΩB5ΩC15ΩD6Ω
The resistance of a heater coil is 110Ω. A resistance R is connected in parallel with it and the combination is joined in series with a resistance of 11Ω to a 220V main line. The heater operates with a power of 110W. The value of R in Ω is
View SolutionTwo resistors having resistance 4 Ω and 6 Ω are connected in parallel. Find their equivalent resistance.
View SolutionThere are n similar conductors each of resistance R . The resultant resistance comes out to be x when connected in parallel. If they are connected in series, the resistance comes out to be
View SolutionThree resistors of 2Ω,3Ω and 4Ω are connected in
parallel. Draw the arrangement and find the equivalent resistance in each case.
View SolutionTwo equal resistors are connected in series. Draw the circuit diagram for determining the resultant resistance.
View SolutionThe resistance 4R,16R,64R....∞ are connected in series. Find their equivalent resistance.
View SolutionThree wires each have resistance 2Ω, if we connect 2 in series with one parallel to the combination the equivalent resistance is
View Solution
