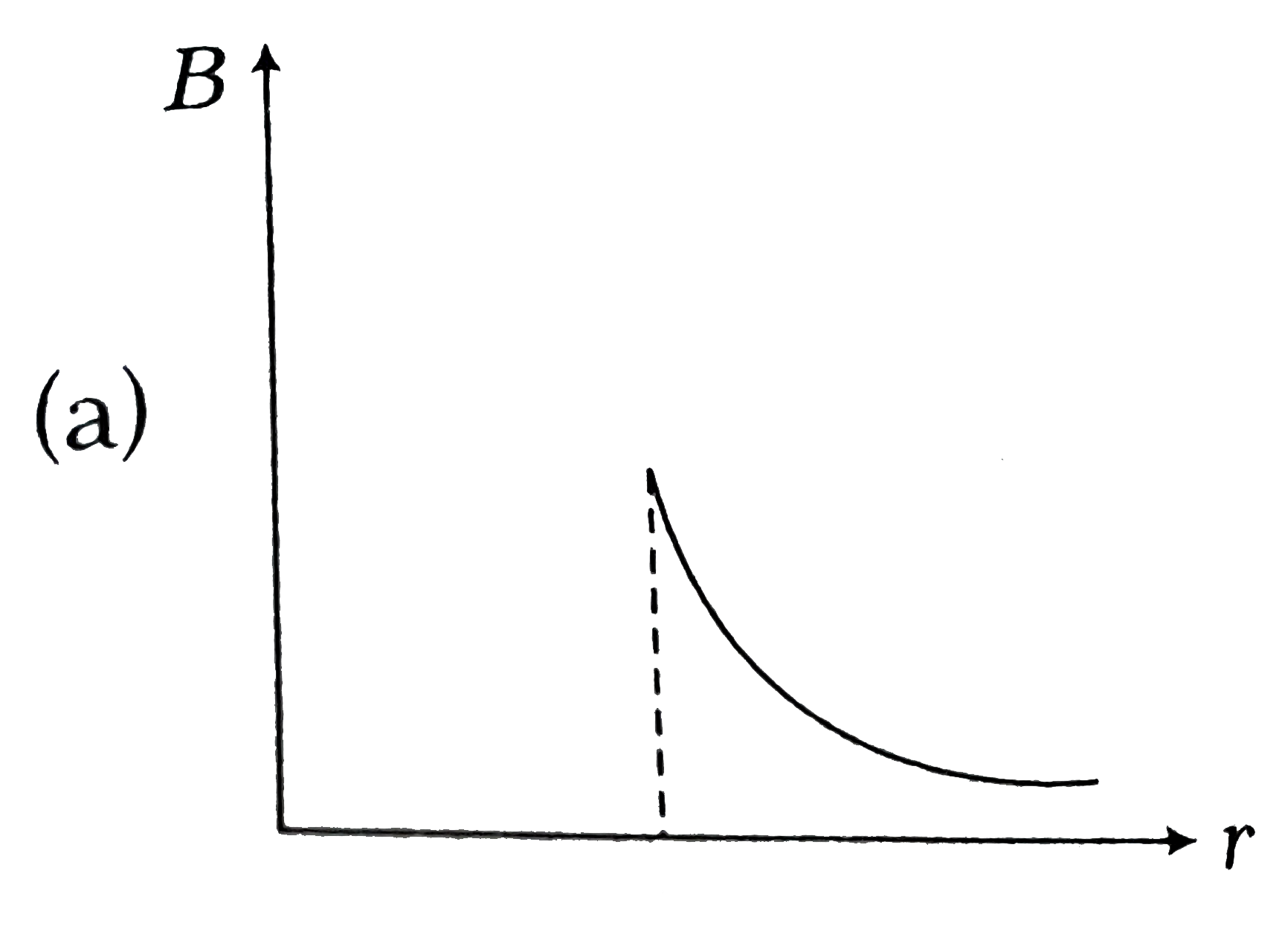
A long thin hollow metallic cylinder of radius 'R' has a current i ampere. The magnetic induction 'B' -away from the axis at a distance r from the axis varies as shown in
The correct Answer is:A
To solve the problem of finding the magnetic induction B at a distance r from the axis of a long thin hollow metallic cylinder carrying a current i, we can follow these steps:
1. Understanding the Setup:
- We have a long thin hollow metallic cylinder with radius R carrying a current i.
- We need to determine the magnetic induction B at a distance r from the axis of the cylinder.
2. Applying Ampere's Circuital Law:
- According to Ampere's Circuital Law, the line integral of the magnetic field B around a closed loop is equal to the permeability of free space μ0 times the current I enclosed by that loop.
- Mathematically, this is expressed as:
∮B⋅dl=μ0Ienc
3. Finding the Magnetic Field Inside the Cylinder:
- For a point inside the hollow cylinder (where r<R), the enclosed current Ienc=0 because there is no current flowing through the area enclosed by the loop.
- Thus, applying Ampere's Law:
∮B⋅dl=0⟹B=0for r<R
4. Finding the Magnetic Field Outside the Cylinder:
- For a point outside the hollow cylinder (where r>R), the entire current i is enclosed by the loop.
- The magnetic field B at a distance r from the axis can be calculated as:
B⋅(2πr)=μ0i
- Rearranging gives:
B=μ0i2πrfor r>R
5. Summarizing the Results:
- The magnetic field B is:
- B=0 for r<R
- B=μ0i2πr for r>R
6. Graphical Representation:
- The magnetic field B is zero inside the cylinder and decreases inversely with distance r outside the cylinder.
- Thus, the graph of B versus r will show B=0 for r<R and a hyperbolic decrease for r>R.
- We have a long thin hollow metallic cylinder with radius R carrying a current i.
- We need to determine the magnetic induction B at a distance r from the axis of the cylinder.
- According to Ampere's Circuital Law, the line integral of the magnetic field B around a closed loop is equal to the permeability of free space μ0 times the current I enclosed by that loop.
- Mathematically, this is expressed as:
∮B⋅dl=μ0Ienc
- For a point inside the hollow cylinder (where r<R), the enclosed current Ienc=0 because there is no current flowing through the area enclosed by the loop.
- Thus, applying Ampere's Law:
∮B⋅dl=0⟹B=0for r<R
- For a point outside the hollow cylinder (where r>R), the entire current i is enclosed by the loop.
- The magnetic field B at a distance r from the axis can be calculated as:
B⋅(2πr)=μ0i
- Rearranging gives:
B=μ0i2πrfor r>R
- The magnetic field B is:
- B=0 for r<R
- B=μ0i2πr for r>R
- The magnetic field B is zero inside the cylinder and decreases inversely with distance r outside the cylinder.
- Thus, the graph of B versus r will show B=0 for r<R and a hyperbolic decrease for r>R.
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Assertion and reason
20 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following
4 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Check point
54 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
A circular coil of wire of radius 'r' has 'n' turns and carries a current 'I'. The magnetic induction (B) at a point on the axis of the coil at a distance √3r from its centre is
View SolutionA thin but long, hollow, cylindrical tube of radius r carries a current i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
View SolutionElectric current is passing unfiormly through a solid cylinderical wire of radius R. The current I passing through circular cross-section of radius r measured from the axis of the cylinder (r<R) varies as shown in
View SolutionA current l is flowing through a long straight solid conductor of radius R = 4 cm. Magnetic field at a distance 2 cm from the axis of conductor is B0 The distance from the axis, where magnetic field is 1.5 B0 is (current density is uniform)
View SolutionFigure shows a long and thin strip of width b which carries a current I. Find magnetic induction due to the current in strip at point P located at a distance r from the strip in the plane of strip as shown in figure-4.35.

View SolutionFigure shows the cross-sectional view of the hollow cylindrical conductor with inner radius 'R' and outer radius '2R', cylinder carrying uniformly distributed current along it's axis. The magnetic induction at point 'P' at a distance 3R2 from the axis of the cylinder will be
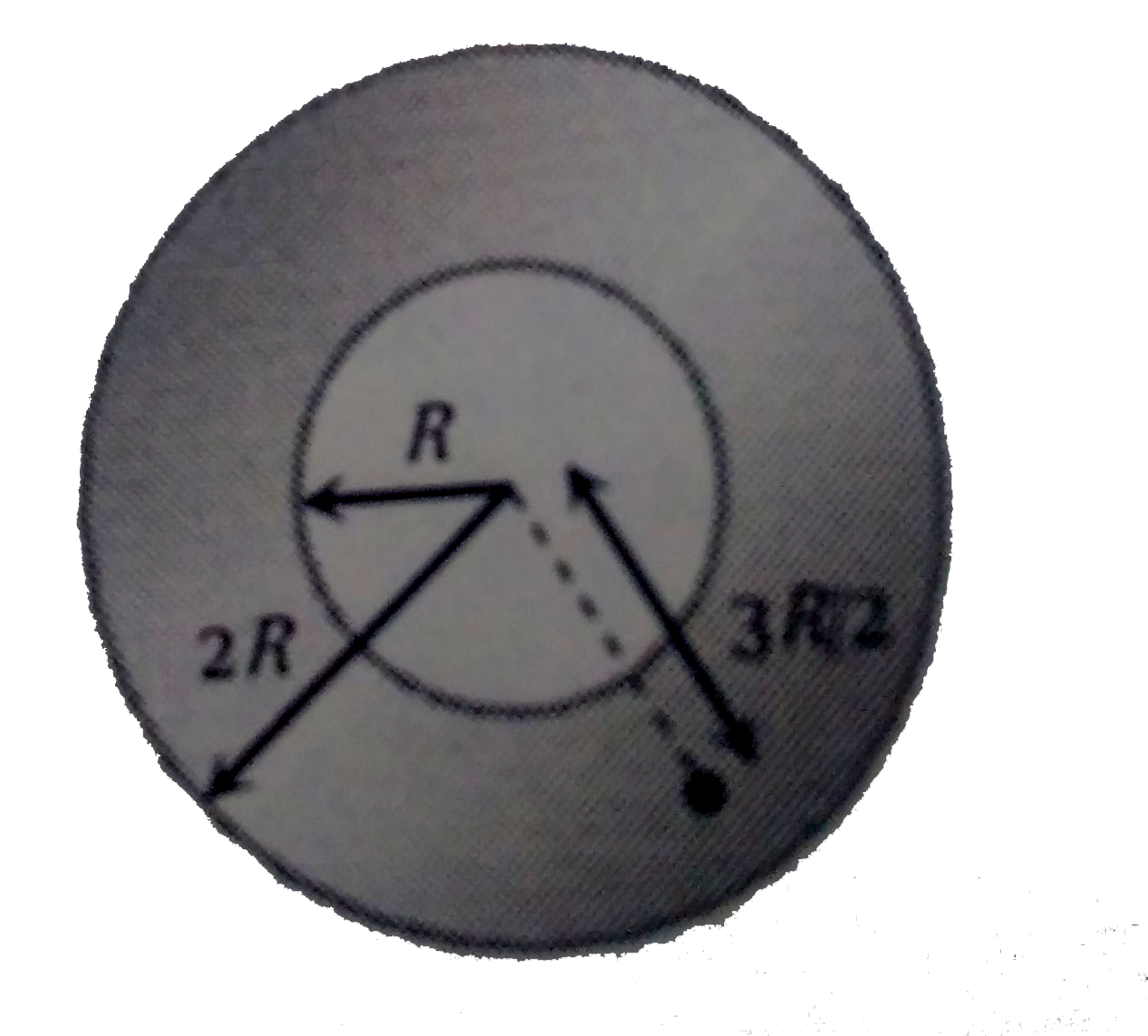
View SolutionA circular coil of radius R carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance r from the centre of the coil, such that r>>R, varies as
View SolutionA circular coil of radius R carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance r from the centre of the coil, such that r>>R, varies as
View SolutionA long cylinder of wire of radius 'a' carries a current i distributed uniformly over its cross section. If the magnetic fields at distances r<aandR>a from the axis have equal magnitude, then
View SolutionAn infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R/2 with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electric field at the point P, which is at a distance 2R form the axis of the cylinder, is given by the expression 23rR16ke0 . The value of k is .
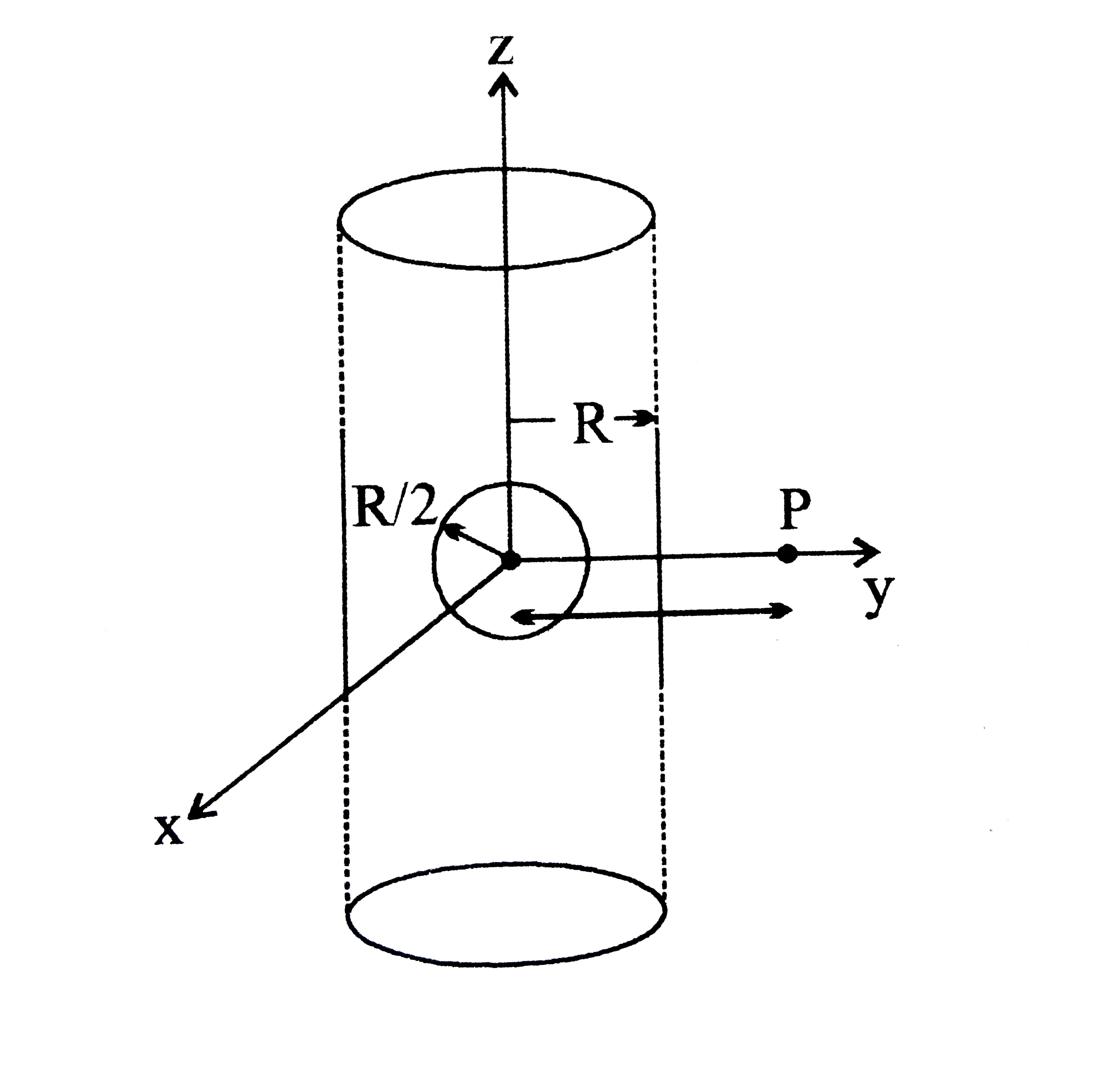 .
.
View Solution
