From amongst the following curves, which one shows the variation of the velocity v with time t for a small sized spherical body falling vertically in a long column of a viscous liquid
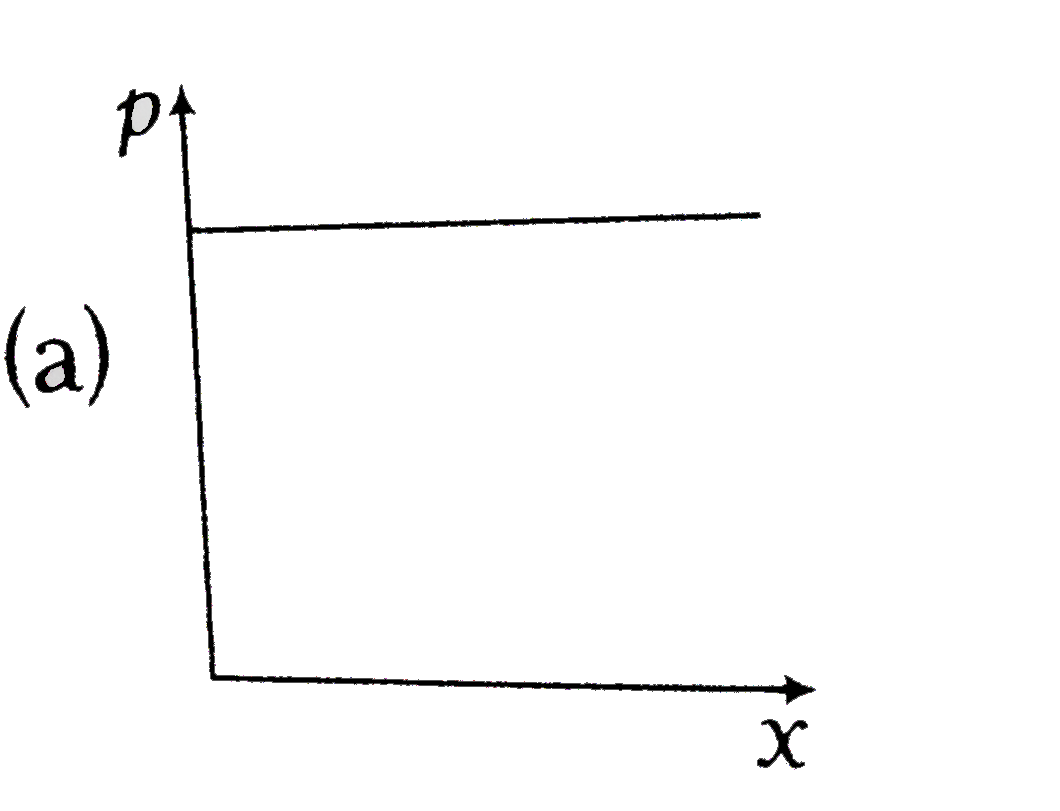

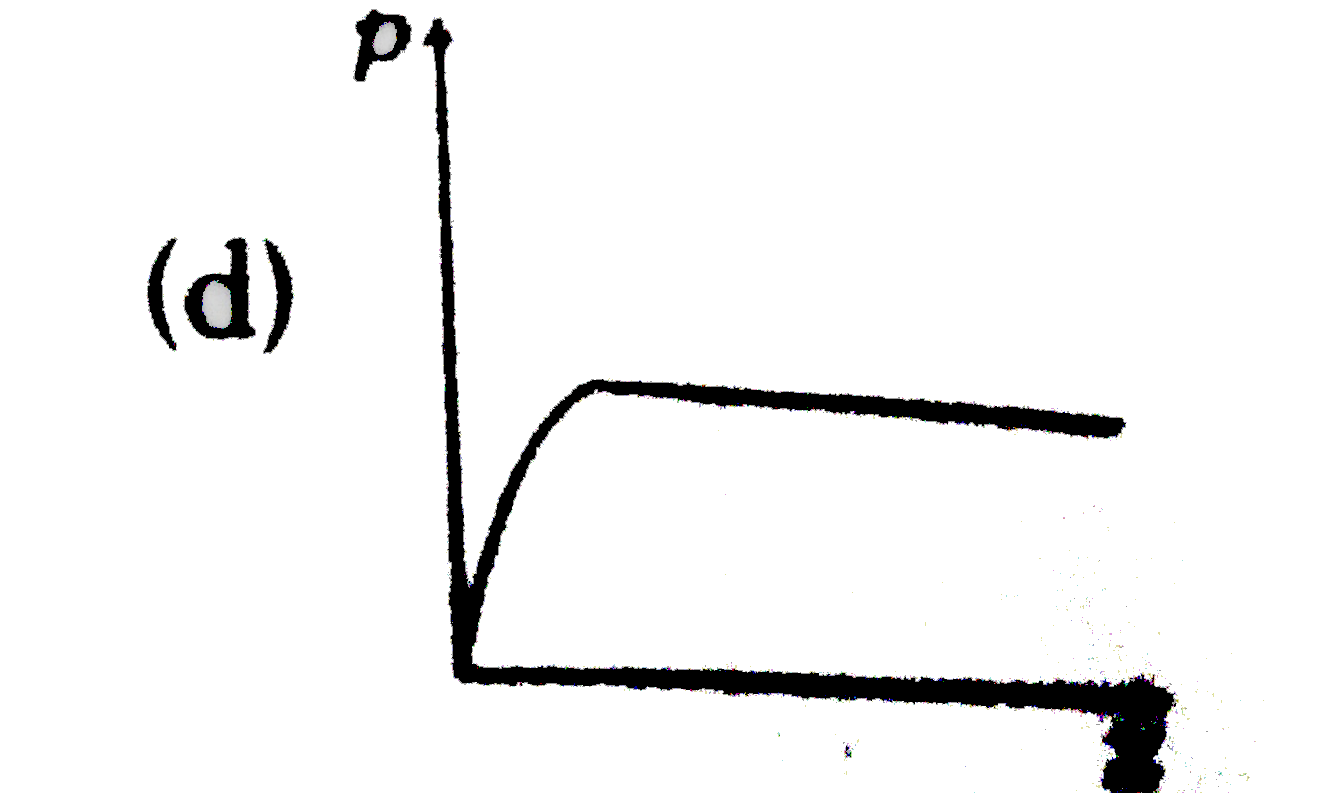
The correct Answer is:D
To determine the variation of the velocity v with time t for a small-sized spherical body falling vertically in a long column of a viscous liquid, we can analyze the motion of the body under the influence of gravity and viscous drag.
1. Understanding the Forces Acting on the Body:
- When a small spherical body is released in a viscous liquid, two main forces act on it:
- The gravitational force Fg=mg (downward).
- The viscous drag force Fd (upward), which opposes the motion.
2. Newton's Second Law:
- According to Newton's second law, the net force acting on the body is given by:
Fnet=Fg−Fd
- This net force causes the body to accelerate.
3. Initial Acceleration:
- Initially, when the body is released, the gravitational force is much greater than the drag force, leading to a net downward force. Therefore, the body accelerates downward.
4. Increasing Velocity:
- As the body falls, its velocity increases, and consequently, the drag force Fd (which is proportional to the velocity) also increases. This can be expressed as:
F_d = kv \quad \text{(where k is a constant)}
5. Reaching Terminal Velocity:
- Eventually, the drag force will equal the gravitational force:
mg=kvt
- At this point, the net force becomes zero, and the body stops accelerating. The velocity at this point is called the terminal velocity vt.
6. Graphical Representation:
- The graph of velocity v versus time t will show:
- An initial increase in velocity (which may appear parabolic due to acceleration).
- A plateau where the velocity becomes constant (terminal velocity).
7. Conclusion:
- The correct curve that represents this behavior is one that starts from zero, increases initially, and then levels off to a constant value. This corresponds to option B.
Final Answer:
The curve that shows the variation of the velocity v with time t for a small-sized spherical body falling vertically in a long column of a viscous liquid is option B.
- When a small spherical body is released in a viscous liquid, two main forces act on it:
- The gravitational force Fg=mg (downward).
- The viscous drag force Fd (upward), which opposes the motion.
- According to Newton's second law, the net force acting on the body is given by:
Fnet=Fg−Fd
- This net force causes the body to accelerate.
- Initially, when the body is released, the gravitational force is much greater than the drag force, leading to a net downward force. Therefore, the body accelerates downward.
- As the body falls, its velocity increases, and consequently, the drag force Fd (which is proportional to the velocity) also increases. This can be expressed as:
F_d = kv \quad \text{(where k is a constant)}
- Eventually, the drag force will equal the gravitational force:
mg=kvt
- At this point, the net force becomes zero, and the body stops accelerating. The velocity at this point is called the terminal velocity vt.
- The graph of velocity v versus time t will show:
- An initial increase in velocity (which may appear parabolic due to acceleration).
- A plateau where the velocity becomes constant (terminal velocity).
- The correct curve that represents this behavior is one that starts from zero, increases initially, and then levels off to a constant value. This corresponds to option B.
The curve that shows the variation of the velocity v with time t for a small-sized spherical body falling vertically in a long column of a viscous liquid is option B.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Taking it together
157 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.2
10 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Knowledge Check
The terminal velocity of small sized spherical body of radius r falling veertically in a viscous liquid is given by a following proportionality
A1r2B1rCrDr2
Which one of the following graphs represents the variation of electric field with distance r from the centre of a charged spherical conductor of radius R?
View SolutionThe terminal velocity v of a spherical ball of lead of radius R falling through a viscous liquid varies with R such that
View SolutionWhich of the following option correctly describes the variation of the speed and acceleration 'a' of a point mass falling vertically in a viscous medium that applies a force F=−kv, where 'k' is constant, on the body?
(Graphs are schematic and drawn to scale)
View SolutionA batsman hits a sixes and the ball touches the ground outside the cricket ground. Which of the following graph describes the variation of the cricket ball's vertical velocity v with time between the time t1 as it hits the bat and time t2 when it touches the ground?
View SolutionThe curve drawn below shows the variations of P as a function of 1/V for a fixed mass and temperature of an ideal gas. It follows from the curve that:
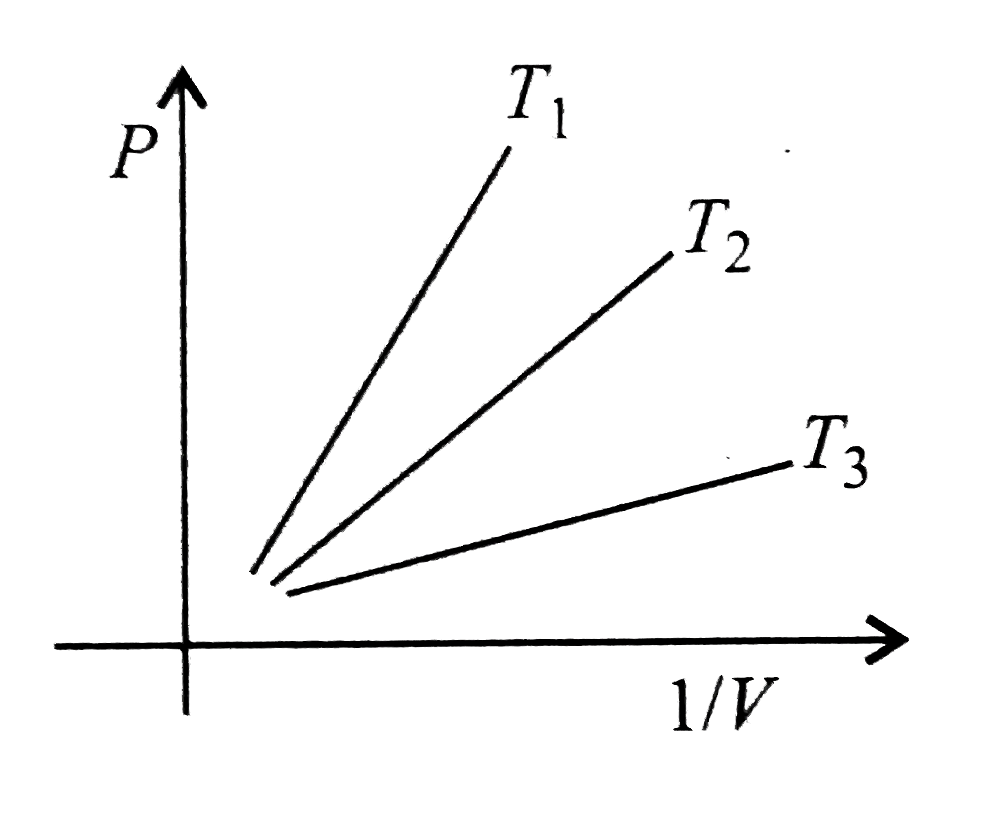
View SolutionWhich one of the following graphs in figure shows the variation of photoelectric current (I) with voltage (V) between the electrodes in a photoelectric cell?
View SolutionWhich of the following velocity-time graphs shows a realistic situation for a body in motion ?
View Solution
