A rectangular loop of length 'l' and breadth 'b' is placed at a distance of x from an infinitely long wire carrying current 'i' such that the direction of current is parallel to breadth. If the loop moves away from the current wire in a direction perpendicular to it with a velocity 'v', the magnitude of the e.m.f. in the loop is: (μ0= permeability of free space)
μ0iv2πx(l+bb)
μ0i2v4π2xlog(bl)
μ0ilbv2πx(l+x)
μ0ilbv2πlog(x+lx)
The correct Answer is:C
To solve the problem, we need to determine the induced electromotive force (e.m.f.) in a rectangular loop that is moving away from an infinitely long wire carrying current. The steps to derive the expression for the induced e.m.f. are as follows:
1. Understand the Setup:
- We have a rectangular loop of length l and breadth b.
- The loop is placed at a distance x from an infinitely long wire carrying current i.
- The loop moves away from the wire with a velocity v in a direction perpendicular to the wire.
2. Identify the Magnetic Field:
- The magnetic field B around a long straight wire carrying current i at a distance r is given by:
\(
B = \frac{\mu_0 i}{2 \pi r}
\)
- For the sides of the loop, we need to consider the magnetic field at two different distances:
- At distance x (for side AD)
- At distance x+l (for side BC)
3. Calculate the Magnetic Fields:
- The magnetic field at distance x (for side AD) is:
\(
B_1 = \frac{\mu_0 i}{2 \pi x}
\)
- The magnetic field at distance x+l (for side BC) is:
\(
B_2 = \frac{\mu_0 i}{2 \pi (x + l)}
\)
4. Determine the Induced e.m.f.:
- The induced e.m.f. (ε) in the loop can be calculated using the formula:
\(
\epsilon = b \cdot (B_1 - B_2) \cdot v
\)
- Substituting the values of B1 and B2:
\(
\epsilon = b \cdot \left(\frac{\mu_0 i}{2 \pi x} - \frac{\mu_0 i}{2 \pi (x + l)}\right) \cdot v
\)
5. Simplify the Expression:
- Factor out common terms:
\(
\epsilon = \frac{\mu_0 i b v}{2 \pi} \left(\frac{1}{x} - \frac{1}{x + l}\right)
\)
- Simplifying the expression inside the parentheses:
\(
\frac{1}{x} - \frac{1}{x + l} = \frac{(x + l) - x}{x(x + l)} = \frac{l}{x(x + l)}
\)
- Therefore, the induced e.m.f. becomes:
\(
\epsilon = \frac{\mu_0 i b v l}{2 \pi x (x + l)}
\)
Final Result:
The magnitude of the induced e.m.f. in the loop is:
\(
\epsilon = \frac{\mu_0 i b v l}{2 \pi x (x + l)}
\)
- We have a rectangular loop of length l and breadth b.
- The loop is placed at a distance x from an infinitely long wire carrying current i.
- The loop moves away from the wire with a velocity v in a direction perpendicular to the wire.
- The magnetic field B around a long straight wire carrying current i at a distance r is given by:
\(
B = \frac{\mu_0 i}{2 \pi r}
\)
- For the sides of the loop, we need to consider the magnetic field at two different distances:
- At distance x (for side AD)
- At distance x+l (for side BC)
- The magnetic field at distance x (for side AD) is:
\(
B_1 = \frac{\mu_0 i}{2 \pi x}
\)
- The magnetic field at distance x+l (for side BC) is:
\(
B_2 = \frac{\mu_0 i}{2 \pi (x + l)}
\)
- The induced e.m.f. (ε) in the loop can be calculated using the formula:
\(
\epsilon = b \cdot (B_1 - B_2) \cdot v
\)
- Substituting the values of B1 and B2:
\(
\epsilon = b \cdot \left(\frac{\mu_0 i}{2 \pi x} - \frac{\mu_0 i}{2 \pi (x + l)}\right) \cdot v
\)
- Factor out common terms:
\(
\epsilon = \frac{\mu_0 i b v}{2 \pi} \left(\frac{1}{x} - \frac{1}{x + l}\right)
\)
- Simplifying the expression inside the parentheses:
\(
\frac{1}{x} - \frac{1}{x + l} = \frac{(x + l) - x}{x(x + l)} = \frac{l}{x(x + l)}
\)
- Therefore, the induced e.m.f. becomes:
\(
\epsilon = \frac{\mu_0 i b v l}{2 \pi x (x + l)}
\)
The magnitude of the induced e.m.f. in the loop is:
\(
\epsilon = \frac{\mu_0 i b v l}{2 \pi x (x + l)}
\)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
Shows a long current carrying wire and two rectangular loops moving with of velocity v. Find the direction of current in each loop.
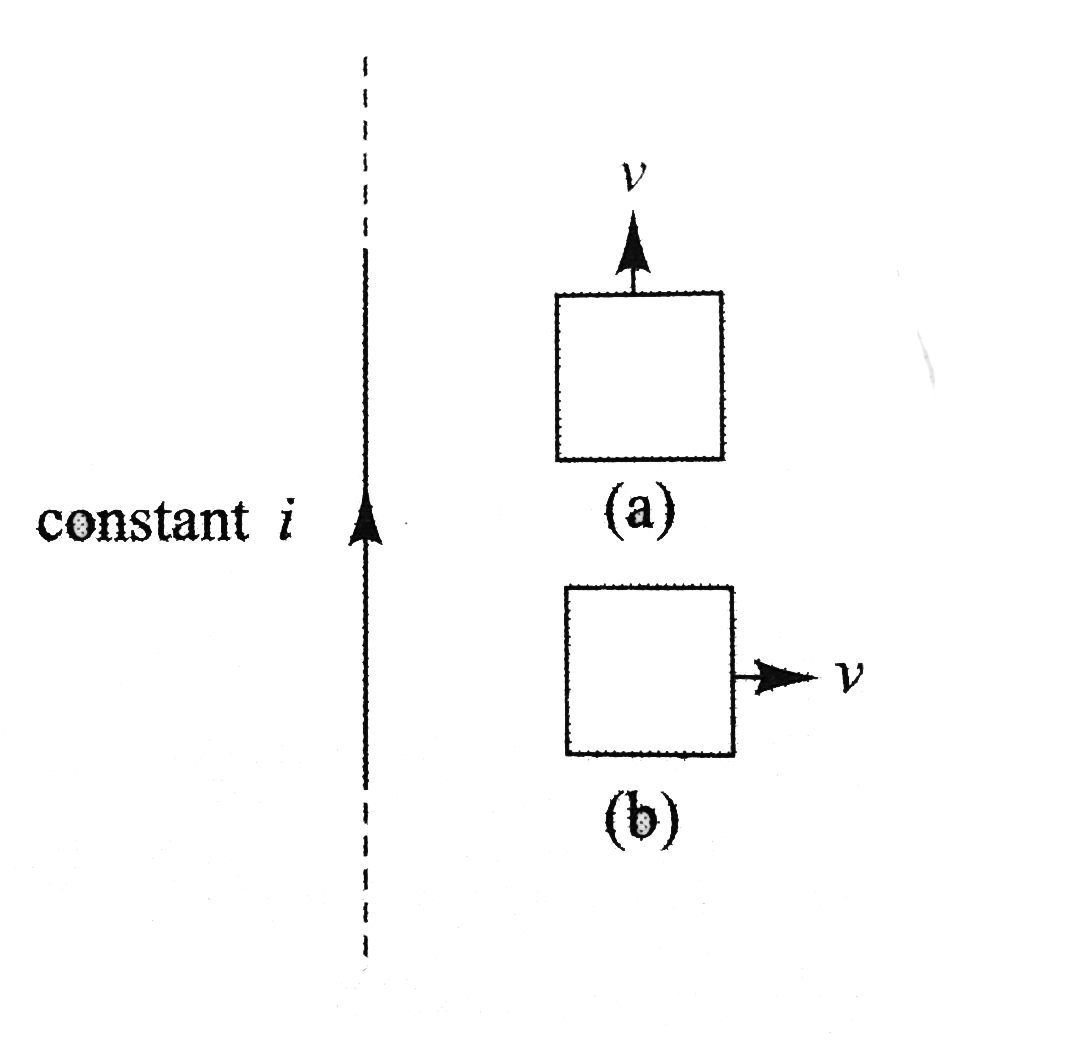
View SolutionShows a long current carrying wire and two rectangular loops moving with of velocity v. Find the direction of current in each loop.

View SolutionShows a long current carrying wire and two rectangular loops moving with of velocity v. Find the direction of current in each loop.

View Solutiona rectangular loop, as shown in Fig. 3.66, moves away from an infinitely long wire carrying a current I. Find the emf induced in the rectangualr loop.

View Solutiona rectangular loop, as shown in Fig. 3.66, moves away from an infinitely long wire carrying a current I. Find the emf induced in the rectangualr loop.

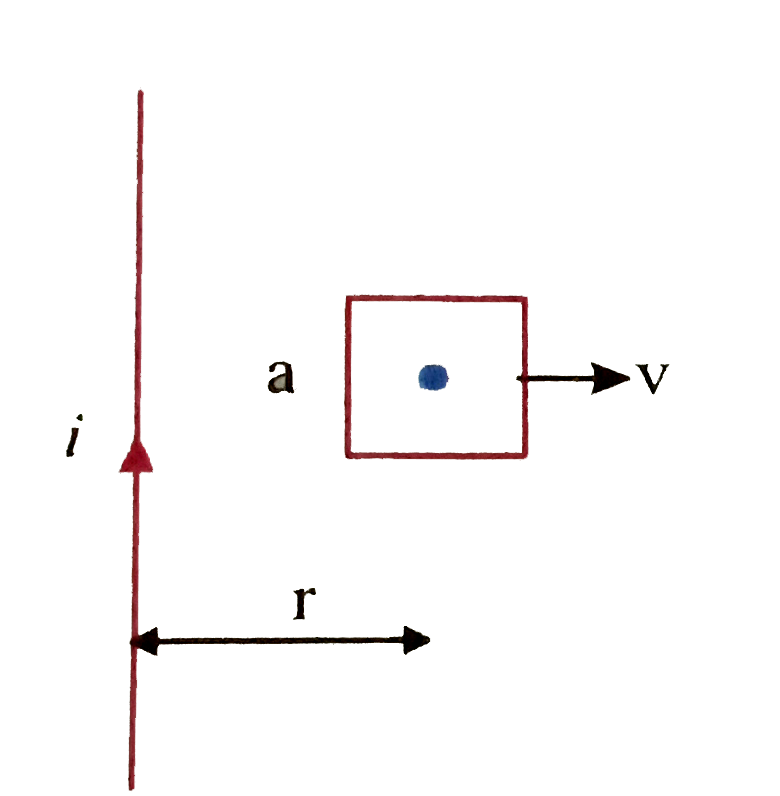
View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from wire where r>>a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f in the loop is
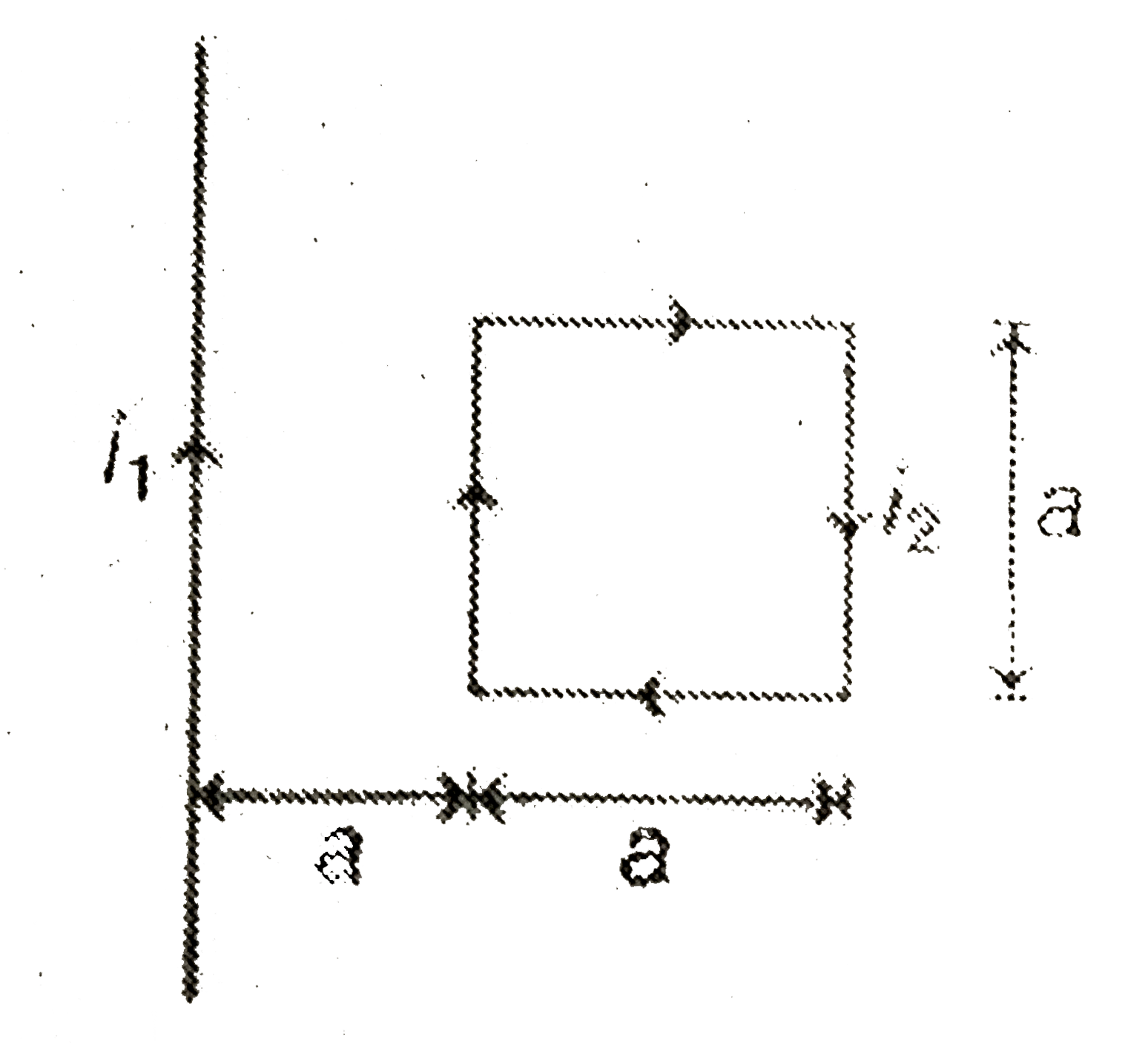
View SolutionA square loop of side a is placed at a distance a length away from a long wire carrying a current I1 . If the loop carries a current I2 as shown in the figure . Then the nature of the nature of the force and its amount is

View SolutionA square loop of 5 cm carrying a current 0.2 A in the clockwise direction is placed at a distance of 10 cm from an infinity long wire carrying a current of 1 A as shown. Calculate (i) the resultant magnetic force and (ii) the torque, if any, acting on the loop.
View SolutionA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
View SolutionA current carrying squre loop is placed near an infinitely long current carrying wire as shown in figure . The loop torque acting on the loop is
View Solution
