Isn't the result of the previous problem in contradiction with the fact that the ideal gas isochore in p-T coordinates is represented by a linear graph, while the iso chore of saturated vapour is nonlinear. ( see 35.3 Fig. 35.2)?
As distinct from an ideal gas, whose molecular concentration (and density) does not change in an isochoric process, the molecular concentration and density) of a saturated vapour rises with temperature because of additional evaporation of the liquid. 22.3. The density of saturated vapour at 55∘Cis104.3g/m3. Therefore at this temperature 8 g of saturated vapour occupies a volume of 810.4.3=7.6×10−3m=7.6 litres. In a smaller volume there will be a precipitation of dew.
Similar Questions
If an additional pressure Δp of a saturated vapour over a convex spherical surface of a liquid is considerably less than the vapour pressure over a plane surface, then Δp=(ρv/ρl)2α/r, where ρv and ρl) are the densities of the vapour and the liquid, α is the surface tension, and r is the radius of curvature of the surface. Using this formula, find the diameter of water droplets at which the saturated vapour pressure exceeds the vapour pressure over the plane surface by η=1.0% at a temperature t=27∘C. The vapour is assumed to be an ideal gas.
View SolutionStraight line on (p - T) graph for an ideal gas represents isochoric process.
If p∝T,V=constant.
View Solution
Knowledge Check
Straight line on (p - T) graph for an ideal gas represents isochoric process.
If p∝T,V=constant.AIf both Assertion and Reason are true and the reason is correct explanation of the Assertion.BIf both Assertion and Reason are true but Reason is not the correct explanation of Assertion.CIf Assertion is true, but the Reason is false.DIf Assertion is false but the Reason is true.A gaseous sample is generally allowed to do only expansion/compression type of work against its surroundings. The work done in case of an irreversible expansion ( in the intermediate stages of expansion/ compression the states of gases are not defined). The work done can be calculated using
dw=−PextdV
while in case of reversible process the work done can be calculated using
dw=-PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process, since
P=nRTV,so,
w=∫dw=−∫VfVinRTV.dV=−nRT In(VfVi)
Since,dw=PdV, so magnitude of work done can also be calculated by calculating the area under the PV curve of the reversible process in PV diagram.
If four identical samples of an ideal gas initially at similar state (P0,V0,T0) are allowed to expand to double their volumes by four different processes.
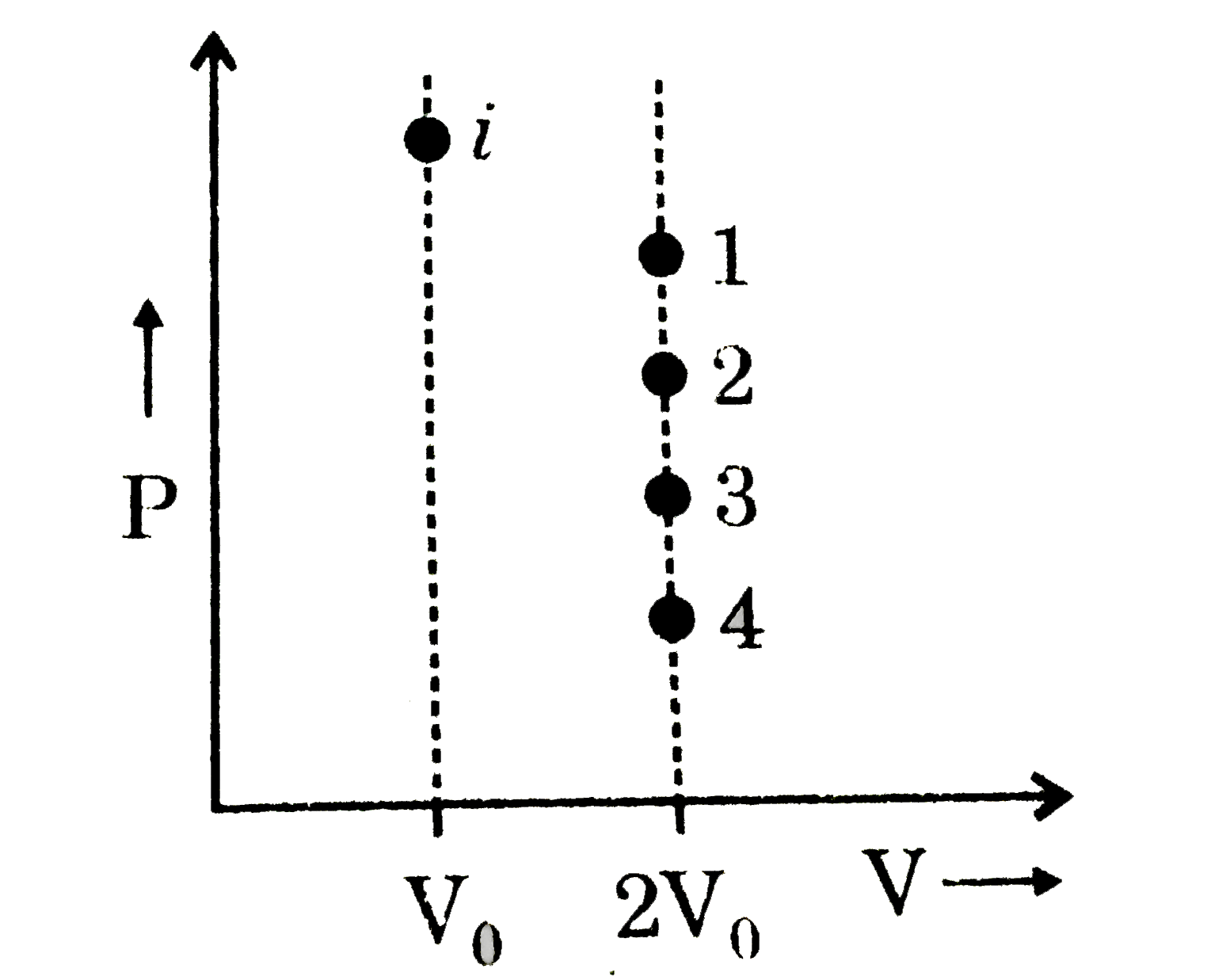
(P)By isothermal irreversible process
(Q) By reversible process having equation P2V= constant
(R) By reversible adiabatic process
(S)By irreversible adiabatic expansion against constant external pressure. Then in the graph shown the final state is represented by four different points then, the correct match can be :A1−P,2−Q,3−R,4−SB1−Q,2−P,3−S,4−RC2−R,3−Q,4−P,1−SD3-Q,1-P,2-S,4-RStraight line on (p - T) graph for an ideal gas represents isochoric process.
If p∝T,V=constant.AStatement-1 is true, statement-2 is true, statement-2 is a correct explanation for statement-1BStatement-1 is true, statement-2 is true, statement-2 is not a correct explanation for statement-1Cstatement-1 is true, statement-2 is falseDstatement-1 is false, statement-2 is true
Here's another paradox from the theory of relativity. Let a spring be perpendicular to the speed of the reference frame. Acted upon by the force F, the spring extends by a length to l0=F0/k. As is well known, transition from one reference frame to another leaves the lateral dimensions unaltered (see Problem 6.1), therefore != lo- Isn't this in contradiction with the fact that as a result of such a transition the lateral force changes in accordance with the law F=F0√1−v2/c2?
View SolutionHere's another paradox from the theory of relativity. Let a spring be perpendicular to the speed of the reference frame. Acted upon by the force F, the spring extends by a length to l0=F0/k. As is well known, transition from one reference frame to another leaves the lateral dimensions unaltered (see Problem 6.1), therefore != lo- Isn't this in contradiction with the fact that as a result of such a transition the lateral force changes in accordance with the law F=F0√1−v2/c2?
View SolutionAssertion: Straight line on (p - T) graph for an ideal gas represents isochoric process.
Reason: If p∝T,V=constant.
View SolutionA gaseous sample is generally allowed to do only expansion/compression type work against its surroundings The work done in case of an irreversible expansion ( in the intermediate stages of expansion/compression the states of gases are not defined). The work done can be calculated using
dw=−PextdV
while in case of reversible process the work done can be calculated using
dw=−PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process. Since P=nRTV, so
w=∫dW=−vf∫vinRTV.dV=−nRTln(VfVi)
Since dw=PdV so magnitude of work done can also be calculated by calculating the area under the PV curve of the reversible process in PV diagram.
If four identical samples of an ideal gas initially at similar state (P0,V0,T0) are allowed to expand to double their volumes by four different process.
I: by isothermal irreversible process
II: by reversible process having equation P2V= constant
III. by reversible adiabatic process
IV. by irreversible adiabatic expansion against constant external pressure.
Then, in the graph shown in the final state is represented by four different points then, the correct match can be
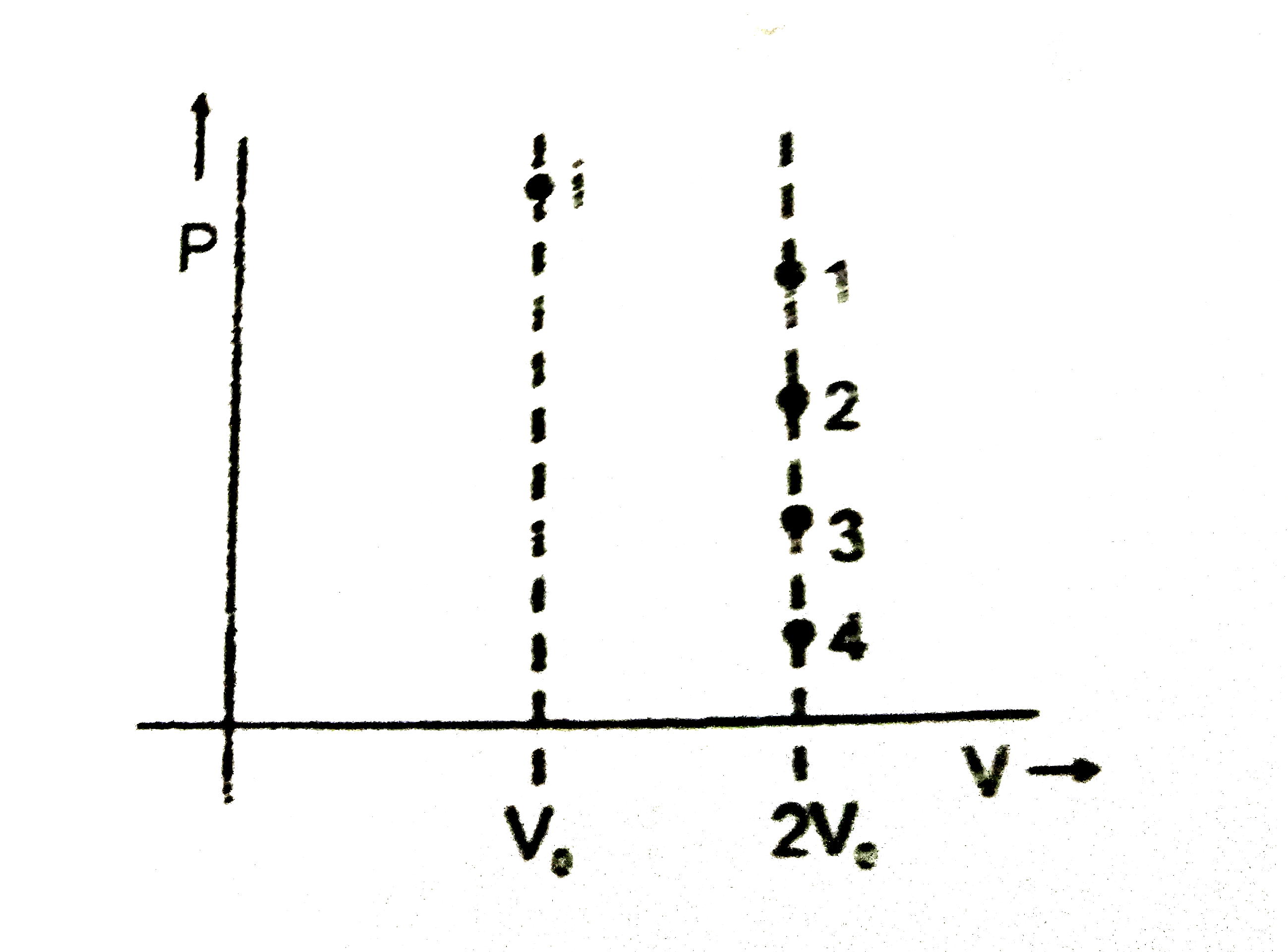
View SolutionThe system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at TK. Standard vapour pressures of A and B are P0A and P0B, respectively, at TK. We collect the vapour of A and B in two containers of volume V, first container is maintained at 2TK and second container is maintained at 3T/2. At the temperature greater than TK, both A and B exist in only gaseous form.
We assume than collected gases behave ideally at 2TK and there may take place an isomerisation reaction in which A gets converted into B by first-order kinetics reaction given as:
Ak−−→B, where k is a rate constant.
In container (II) at the given temperature 3T/2, A and B are ideal in nature and non reacting in nature. A small pin hole is made into container. We can determine the initial rate of effusion of both gases in vacuum by the expression

r=K.P√M0
where P= pressure differences between system and surrounding
K= positive constant
M0= molecular weight of the gas
If partial vapour pressure of A is twice that of partial vapour pressure of B and total vapour pressure 2 atm at TK, where T=50K and V=8.21L, then the number of moles of A and B in vapour phase is:
View Solution
