An ice skater moving at comes to a halt in on a ice surface. Calculate the coefficient of friction between the ice and the skater ?
To solve the problem of finding the coefficient of friction between the ice and the skater, we can follow these steps:
Step 1: Identify the known values
- Initial velocity (u) = 10 m/s
- Final velocity (v) = 0 m/s (since the skater comes to a halt)
- Distance (s) = 100 m
Step 2: Use the equation of motion
We can use the equation of motion:
v2−u2=2as
Where:
- v = final velocity
- u = initial velocity
- a = acceleration
- s = distance
Step 3: Substitute the known values into the equation
Substituting the known values:
02−(10)2=2a(100)
This simplifies to:
−100=200a
Step 4: Solve for acceleration (a)
Rearranging the equation gives:
a=−100200=−0.5m/s2
(Note: The negative sign indicates that the acceleration is in the opposite direction of the motion, which is expected since the skater is decelerating.)
Step 5: Relate acceleration to friction
The frictional force is what causes the skater to decelerate. The equation for friction is:
f=μN
Where:
- f = frictional force
- μ = coefficient of friction
- N = normal force
In this case, the normal force N is equal to the weight of the skater, which is mg (mass times gravitational acceleration).
Step 6: Set up the equation for motion
The frictional force also equals mass times acceleration:
f=ma
Setting the two expressions for friction equal gives:
ma=μmg
Step 7: Cancel mass (m) from both sides
Assuming the mass of the skater is not zero, we can cancel m:
a=μg
Step 8: Solve for the coefficient of friction (μ)
We already calculated a=−0.5m/s2 and g=9.8m/s2. Plugging these values into the equation gives:
−0.5=μ(9.8)
Step 9: Rearranging to find μ
Rearranging the equation to solve for μ:
μ=−0.59.8
Step 10: Calculate μ
Calculating the value:
μ≈−0.59.8≈−0.051
Since the coefficient of friction cannot be negative, we take the absolute value:
μ≈0.051
Final Answer
The coefficient of friction between the ice and the skater is approximately 0.051.
---
- Initial velocity (u) = 10 m/s
- Final velocity (v) = 0 m/s (since the skater comes to a halt)
- Distance (s) = 100 m
We can use the equation of motion:
v2−u2=2as
Where:
- v = final velocity
- u = initial velocity
- a = acceleration
- s = distance
Substituting the known values:
02−(10)2=2a(100)
This simplifies to:
−100=200a
Rearranging the equation gives:
a=−100200=−0.5m/s2
(Note: The negative sign indicates that the acceleration is in the opposite direction of the motion, which is expected since the skater is decelerating.)
The frictional force is what causes the skater to decelerate. The equation for friction is:
f=μN
Where:
- f = frictional force
- μ = coefficient of friction
- N = normal force
The frictional force also equals mass times acceleration:
f=ma
ma=μmg
Assuming the mass of the skater is not zero, we can cancel m:
a=μg
We already calculated a=−0.5m/s2 and g=9.8m/s2. Plugging these values into the equation gives:
−0.5=μ(9.8)
Rearranging the equation to solve for μ:
μ=−0.59.8
Calculating the value:
μ≈−0.59.8≈−0.051
Since the coefficient of friction cannot be negative, we take the absolute value:
μ≈0.051
The coefficient of friction between the ice and the skater is approximately 0.051.
Topper's Solved these Questions
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Additional solved examples
9 Videos
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Conceptual short answer questions with answer
9 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
12 Videos
- GRAVITATIONBOOK - ICSECHAPTER - GRAVITATIONEXERCISE - FROM THE HUBBLE TELESCOP
2 Videos
Similar Questions
The time taken for an ice block to slide down on inclined surface of inclination 60∘ is 1-2 times the time taken by the same ice block to slide down a frictionless inclined plane of the same inclination. Calculate the coefficient of friction between ice and the inclined plane ?
View SolutionA piece of ice slides down a 45∘ incline in twice the time it takes to slide down a frictionless 45∘ incline . What is the coefficient of friction between the ice and the incline ? .
View Solution
Knowledge Check
A block slides with a velocity of 10 m/sec. on a rough horizontal surface. It comes to rest after covering of 50 m. If g is 10 m/sec2, then the coefficient of dynamic friction between the block and surface is
A1B10C2D0.1
Two blocks of masses 2kg and M are at rest on an inclined plane and are separated by a distance of 6.0m as shown. The coefficient of friction between each block and the inclined plane is 0.25. The 2kg block is given a velocity of 10.0m/s up the inclined plane. It collides with M, comes back and has a velocity of 1.0m/s when it reaches its initial position. The other block M after the collision moves 0.5m up and comes to rest. Calculate the coefficient of restitution between the blocks and the mass of the block M.
[Take sinθ=tanθ=0.05 and g=10m/s2]
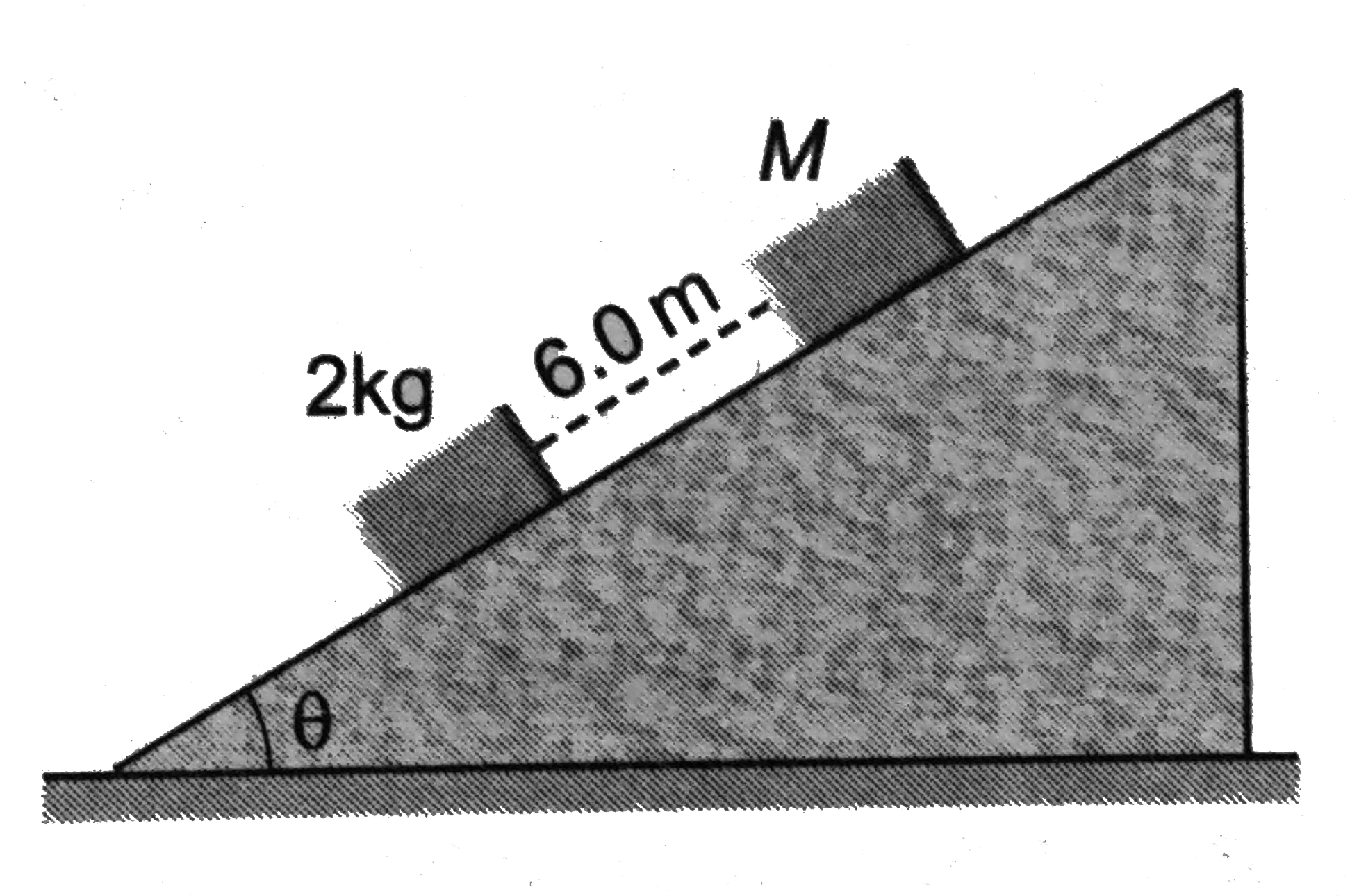
View SolutionA force of 147N is required to just slide a sledgeweighing 500N over a surface of ice. Calculate the coefficient the coefficient of friction between the surface of contact of the sledge and the ice.
View SolutionA block of mass 10 kg slides down on an incline 5 m long and 3 m high. A man pushes up on the ice block parallel to the incline so that it slides down at constant speed. The coefficient of friction between the ice and the incline is 0.1. Find :
(a) the work done by the man on the block.
(b) the work done by gravity on the block.
(c) the work done by the surface on the block.
(d) the work done by the resultant forces on the block.
(e) the change in K.E. of the block.
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionThe velocity - time (V - t) graph of an object of mass 2 kg is as shown in figure while it is moving on a rough horizontal surface. The coefficient of friction between object and the surface is (g=10ms2)
View SolutionA skater of mass m standing on ice throws a stone of mass M with a velocity of v in a horizontal direction. The distance over which the skater will move back (the coefficient of friction between the skater and the ice is μ)
View SolutionA stone of 1kg is thrown with a velocity of 20ms−1 across the frozen surface of lake and comes to rest after travelling a distance of 50m. What is the force of friction between the stone and the ice?
View Solution
