m द्रव्यमान की एक गेंद को हल्की अविस्तारणीय L लंबाई की डोरी की सहायता से एक स्थिर बिंदु O से लटकाया गया है। गेंद को निम्नतम बिंदु पर चाल u इस प्रकार दी जाती है कि यह चित्र में दर्शाये अनुसार O केंद्र वाले ऊर्ध्वाधर वृत्त को पूरा कर लेता है। माना AB वृत्तीय पथ का एक व्यास है जो ऊर्ध्वाधर से कोण बनता है। (g गुरूत्वीय त्वरण है)
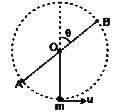
माना तथा डोरी में उस समय तनाव है जब डोरी क्रमशः बिंदु A एवं बिंदु B पर है । तो का मान होगा।
इनमें से कोई नहीं
The correct Answer is:A

स्थिति A एवं B पर गतिज ऊर्जाओं में अंतर
………1
……..2
सभी 1 एवं 2 से
A एवं B पर त्वरण के घटक चित्र में प्रदर्शित है।
Topper's Solved these Questions
Similar Questions
दो ब्लॉक A तथा B क्षैतिज चिकनी सतह पर चित्रानुसार रखे गये है जिन पर समान परिमाण के दो बल चित्रानुसार लगाये गये है। प्रत्येक ब्लॉक का त्वरण ज्ञात कीजिये ( g=10m/s2 लीजिये)
 View Solution
View Solutionएक 2 kg की खिलौना कार x अक्ष के अनुदि । गति कर सकती है। ग्राफ बल Fx को प्रदर्शित करता है, जो समय t = 0 पर विराम पर कार पर लग्न प्रारम्भ होता है | t= 10 s पर कार एक वेग है:
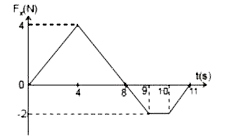 04:29View Solution
04:29View Solutionदरअसल शुरू से ही था हमारे आदेशों में कही एक जानी दुश्मन कि घर को बचाना है लूटेरों से शहर को बचाना है नदियों से देश को बचाना है , देश के दुश्मनों से बचाना है - नदियों को नाला हो जाने से हवा को धुआँ हो जाने से खाने को जहर हो जाने से : बचाना है - जंगल को मरुस्थल हो जाने से , बचाना है - मनुष्य को , जंगल हो जाने से । शब्द - सारिणी की सहायता से समान अर्थ के शब्द ढूढ़कर लीखिए :
04:22View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
05:53View Solutionएक बिंदु इस प्रकार गमन करता है कि उसकी बिंदु (3,4) से दुरी बिंदु (−3,−4) से उसकी दूरी की तिगुनी रहती है । उसका बिन्दुपथ ज्ञात कीजिए ।
10:07View Solutionतीन थेलो A ,B तथा C में क्रमश : 6 लाल ,4 सफ़ेद ,2 लाल 6 सफ़ेद तथा 1 लाल 5 सफ़ेद गेंद है एक थैले का यादृच्छिक रूप से चयन किया गया तथा उसमे से एक गेंद निकाली जो की लाल रंग की थी प्रायिकता ज्ञात कीजिए की यह गेंद थैला A में से निकाली गई है
05:41View Solutionतीन थैलों में रंगीन गेंदें निम्न सारणी में दर्शाये गए तरह से आबंटित की गयी हैं-
 एक थैले को याद्द्च्छ्या चुना गया और फिर उसमें से दो गेंदें निकली गई। यदि गेंद का रंग काला और लाल है तो उसकी क्या प्रायिकता है कि गेंद को थैला I से निकाला गया है?04:37View Solution
एक थैले को याद्द्च्छ्या चुना गया और फिर उसमें से दो गेंदें निकली गई। यदि गेंद का रंग काला और लाल है तो उसकी क्या प्रायिकता है कि गेंद को थैला I से निकाला गया है?04:37View Solutionवह समतल, जो बिन्दुओ (−3,−3,4) तथा (3,7,6) को मिलाने वाले रेखाखण्ड का लंबसमद्विभाजक करता है, निम्न में से किस एक बिंदु से होकर जाता है?
02:36View Solutionवक्र y=xex2 की वह स्पर्श रेख जो बिंदु (1,e) से होकर जाती है, निम्न में से किस बिंदु से भी होकर जाती है ?
02:33View Solutionएक बिंदु p को एक वृत्त के भीतरी भाग से यादृच्छिक रूप से चयन किया जाता है, तो वह, प्रायिकता क्या होगी जिससे यह वस्तुतः वृत्त की परिसीमा के नजदीक होने की बजाय वृत्त के केंद्र से अधिक नजदीक होगा।
01:01View Solutionएक थैले में 3 सफेद और 5 काली गेंदें हैं। थैले के अंदर से बिना देखे एक गेंद निकाली जाती है।
(a) एक सफेद गेंद प्राप्त करने की प्रायिकता क्या है?
(b) एक काली गेंद प्राप्त करने की प्रायिकता क्या है?02:05View SolutionA train travels at a speed of 76 km/hr. If it crosses a pole in 36 sec. The length of the train is:
एक ट्रेन 76 किमी/घंटा की चाल से चलती है | यदि यह एक खंभे को 36 सेकंड में पार करती है, तो ट्रेन की लंबाई क्या है ?05:20View SolutionIn a circle centred at O, AB is a chord and C is any point on AB, such that OC is perpendicular to AB. If the length of the chord is 16 cm and OC = 6 cm, the radius of circle is : O केंद्र वाले एक वृत्त में, AB एक जीवा है और C, AB पर कोई बिंदु है, जैसे OC, AB पर लंबवत है। यदि जीवा की लंबाई 16 सेमी और OC = 6 सेमी है, तो वृत्त की त्रिज्या है:
03:52View SolutionAB is a diameter of a circle with centre O. CB is a tangent to the circle at B. AC intersects the circle at G. If the radius of the circle is 6cm and AG = 8cm, then the length of BC is : AB एक वृत्त का व्यास है जिसका केंद्र O है | CB, B पर वृत्त की स्पर्श रेखा है| AC, वृत्त को G पर काटता है | यदि वृत्त की त्रिज्या 6 सेमी है तथा AG = 8 सेमी है, तो BC की लंबाई ज्ञात करें |
05:24View SolutionIn a circle with centre O, PQR is a tangent at the point Q on it. AB is a chord in the circle parallel to the tangent such that angle BQR= 70^@ . What is the measure of angle AQB ? केंद्र O वाले एक वत्त में, PQR इस पर स्थित बिंदु Q पर एक स्पर्श रेखा है | AB वृत्त में एक जीवा है जो स्पर्श रेखा से इस प्रकार समानांतर है कि angle BQR= 70^@ है | angle AQB का मान ज्ञात करें |
06:52View SolutionA and B are two points on a circle with centre O. AT is a tangent, such that angle BAT = 45^@ .N is a point on OA, such that BN= 10 cm. The length of the median OM of the triangle NOB is: A और B केंद्र O वाले एक वृत्त पर स्थित दो बिंदु हैं | AT एक स्पर्श रेखा है जो इस प्रकार है कि angle BAT = 45^@ है| N, OA पर स्थित एक बिंदु है जो इस प्रकार है कि BN =10 सेमी है | triangle NOB की मध्यिका OM की लंबाई ज्ञात करें |
03:06View Solution

