Consider the circle S:x2+y2−4x−1=0 and the line L:y=3x−1. If the line L cuts the circle at A & B. (i) Length of the chord AB equal (i) The angle subtended by the chord AB in the minor arc of S is (iii). Acute angle between the line L and the circle S is
π4
2π3
3π4
5π6
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Rewrite the equation of the circle in standard form
The given equation of the circle is:
x2+y2−4x−1=0
We can rearrange this equation to find the center and radius of the circle. Completing the square for the x terms:
1. Group the x terms:
(x2−4x)+y2=1
2. Complete the square for x2−4x:
(x−2)2−4+y2=1
(x−2)2+y2=5
From this, we can see that the center of the circle is at (2,0) and the radius r is √5.
Step 2: Find the points of intersection (A and B) of the line and the circle
The equation of the line is given as:
y=3x−1
Substituting this into the circle's equation:
x2+(3x−1)2−4x−1=0
Expanding:
x2+(9x2−6x+1)−4x−1=0
10x2−10x=0
Factoring out 10x:
10x(x−1)=0
Thus, x=0 or x=1.
Now, substituting back to find y:
- For x=0:
y=3(0)−1=−1
So, point A is (0,−1).
- For x=1:
y=3(1)−1=2
So, point B is (1,2).
Step 3: Calculate the length of chord AB
Using the distance formula:
AB=√(x2−x1)2+(y2−y1)2
Where A(0,−1) and B(1,2):
AB=√(1−0)2+(2−(−1))2
=√12+(2+1)2
=√1+9
=√10
Step 4: Find the angle subtended by chord AB at the center of the circle
Using the sine rule:
Let O be the center of the circle (2,0). The distances OA and OB are both equal to the radius √5.
Using the triangle OAB:
- AB=√10
- OA=OB=√5
Using the cosine rule:
AB2=OA2+OB2−2⋅OA⋅OB⋅cos(θ)
10=5+5−2⋅5⋅cos(θ)
10=10−10⋅cos(θ)
10⋅cos(θ)=0
cos(θ)=0
Thus, θ=90∘.
Step 5: Find the acute angle between the line L and the radius at point A
The slope of line L is 3 and the slope of the radius OA can be calculated as:
slope of OA=y2−y1x2−x1=−1−00−2=−1−2=12
Using the formula for the angle between two lines:
tan(ϕ)=∣∣∣m1−m21+m1m2∣∣∣
Where m1=3 (slope of line L) and m2=12:
tan(ϕ)=∣∣
∣∣3−121+3⋅12∣∣
∣∣=∣∣
∣∣62−121+32∣∣
∣∣=∣∣
∣∣5252∣∣
∣∣=1
Thus, ϕ=45∘.
Summary of Answers:
1. Length of chord AB = √10
2. Angle subtended by chord AB at the center = 90∘
3. Acute angle between line L and radius at point A = 45∘
The given equation of the circle is:
x2+y2−4x−1=0
(x2−4x)+y2=1
(x−2)2−4+y2=1
(x−2)2+y2=5
The equation of the line is given as:
y=3x−1
x2+(3x−1)2−4x−1=0
x2+(9x2−6x+1)−4x−1=0
10x2−10x=0
10x(x−1)=0
- For x=0:
y=3(0)−1=−1
So, point A is (0,−1).
y=3(1)−1=2
So, point B is (1,2).
Using the distance formula:
AB=√(x2−x1)2+(y2−y1)2
Where A(0,−1) and B(1,2):
AB=√(1−0)2+(2−(−1))2
=√12+(2+1)2
=√1+9
=√10
Using the sine rule:
Let O be the center of the circle (2,0). The distances OA and OB are both equal to the radius √5.
- AB=√10
- OA=OB=√5
AB2=OA2+OB2−2⋅OA⋅OB⋅cos(θ)
10=5+5−2⋅5⋅cos(θ)
10=10−10⋅cos(θ)
10⋅cos(θ)=0
cos(θ)=0
Thus, θ=90∘.
The slope of line L is 3 and the slope of the radius OA can be calculated as:
slope of OA=y2−y1x2−x1=−1−00−2=−1−2=12
tan(ϕ)=∣∣∣m1−m21+m1m2∣∣∣
Where m1=3 (slope of line L) and m2=12:
tan(ϕ)=∣∣
∣∣3−121+3⋅12∣∣
∣∣=∣∣
∣∣62−121+32∣∣
∣∣=∣∣
∣∣5252∣∣
∣∣=1
1. Length of chord AB = √10
2. Angle subtended by chord AB at the center = 90∘
3. Acute angle between line L and radius at point A = 45∘
Topper's Solved these Questions
- CIRCLE BOOK - ARIHANT MATHS ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise (Single Integer Answer Type Questions)
9 Videos
- CIRCLE BOOK - ARIHANT MATHS ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise (Statement I And Ii Type Questions)
7 Videos
- CIRCLE BOOK - ARIHANT MATHS ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- BIONOMIAL THEOREMBOOK - ARIHANT MATHS ENGLISHCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- COMPLEX NUMBERSBOOK - ARIHANT MATHS ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 8
2 Videos
Similar Questions
Knowledge Check
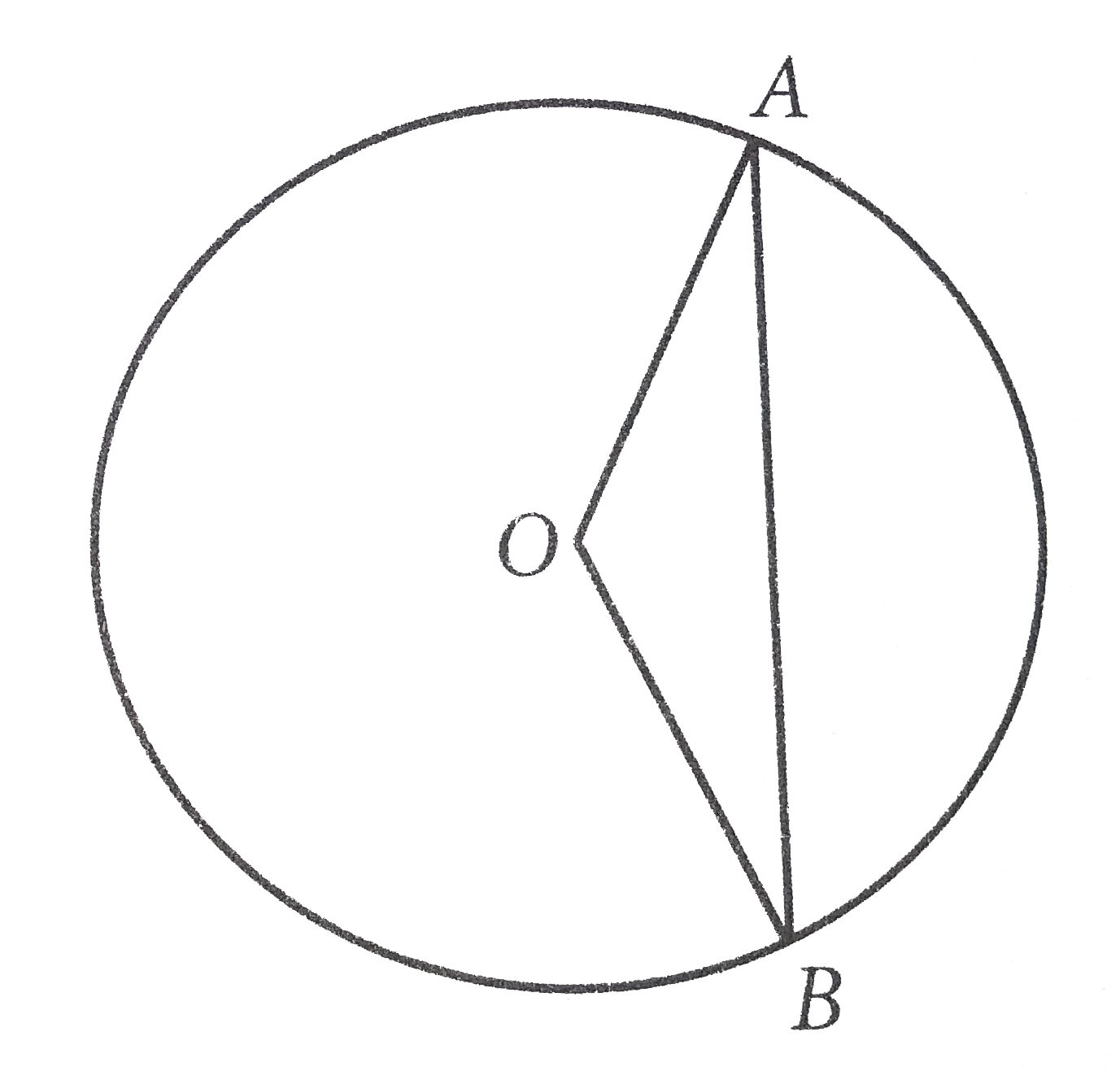
If the radius of the circle above is x, ∠AOB=120∘, and O is the center of the circle, what is the length of chord AB, in terms of x?A√2xB√3xCx√2Dx√3
If the circle x2+y2=a2 cuts off a chord of length 2b from the line y=mx+c, then
View SolutionThe chord of a circle is equal to its radius. The angle subtended by this chord at the minor arc of the circle is
View SolutionIf a chord AB subtends and angle of 60∘ at the centre of a circle, then the angle between the tangents to the circle drawn from A and B is
View Solutionx−y+b=0 is a chord of the circle x2+y2=a2 subtending an angle 600 in the major segment of the circle. Statement 1 : ba=±√2. Statement 2 : The angle subtended by a chord of a circle at the centre is twice the angle subtended by it at any point on the circumference. (A) Both 1 and 2 are true and 2 is the correct explanation of 1 (B) Both 1 and 2 are true and 2 is not a correct explanation of 1 (C) 1 is true but 2 is false (D) 1 is false but 2 is true
View SolutionIf the equation of a given circle is x2+y2=36, then the length of the chord which lies along the line 3x+4y−15=0 is
View SolutionThe acute angle between the line 3x−4y=5 and the circle x2+y2−4x+2y−4=0 is θ . Then 9cosθ=
View SolutionIf the length of focal chord of y2=4ax is l, then find the angle between the axis of the parabola and the focal chord.
View Solution
