[Solved] a parabola

Equation of the circumcircle of a triangle formed by the lines $L_{1} = 0, L_{2} = 0 and L_{3} = 0$ can be written as $L_{1} L_{2} + λ L_{2} L_{3} + μ L_{3} L_{1} = 0$ , where $λ and μ$ are such that coefficient of $x^{2}$ =coefficient of $y^{2}$ and coefficient of xy=0.
$L_{1} L_{2}^{2} + λ L_{2} L_{3}^{2} + μ L_{1}^{2} = 0$ represents

View Solution

Equation of the circumcircle of a triangle formed by the lines $L_{1} = 0, L_{2} = 0 and L_{3} = 0$ can be written as $L_{1} L_{2} + λ L_{2} L_{3} + μ L_{3} L_{1} = 0$ , where $λ and μ$ are such that coefficient of $x^{2}$ =coefficient of $y^{2}$ and coefficient of xy=0.
If $L_{1} L_{2} + λ L_{2} L_{3} + μ L_{3} L_{1} = 0$ is such that $μ = 0 and λ$ is non-zero, then it represents

View Solution

Find the equation of the circle which circumscribes the triangle formed by the lines $x = 0, y = 0 a n d l x + m y = 1 .$

View Solution

Let $l_{1} and l_{2}$ be the two skew lines. If P, Q are two distinct points on $l_{1}$ and R, S are two distinct points on $l_{2}$ , then prove that PR cannot be parallel to QS.

View Solution

Let $L_{1} = 0 and L_{2} = 0$ be two intarecting straight lines. Then the number of points, whose distacne from $L_{1}$ is 2 units and from $L_{2}$ 2 units is

View Solution

Let $l_{1}$ and $l_{2}$ be the two lines which are normal to $y^{2} = 4 x$ and tangent to $x^{2} = - 12 y$ respectively (where, $l_{1} and l_{2}$ are not the x - axis). Then, the product of the slopes of $l_{1} and l_{2}$ is

View Solution

Consider the lines given by
$L_{1} : x + 3 y - 5 = 0$
$L_{2} : 3 x - k y - 1 = 0$
$L_{3} : 5 x + 2 y - 12 = 0$
Match the following lists.
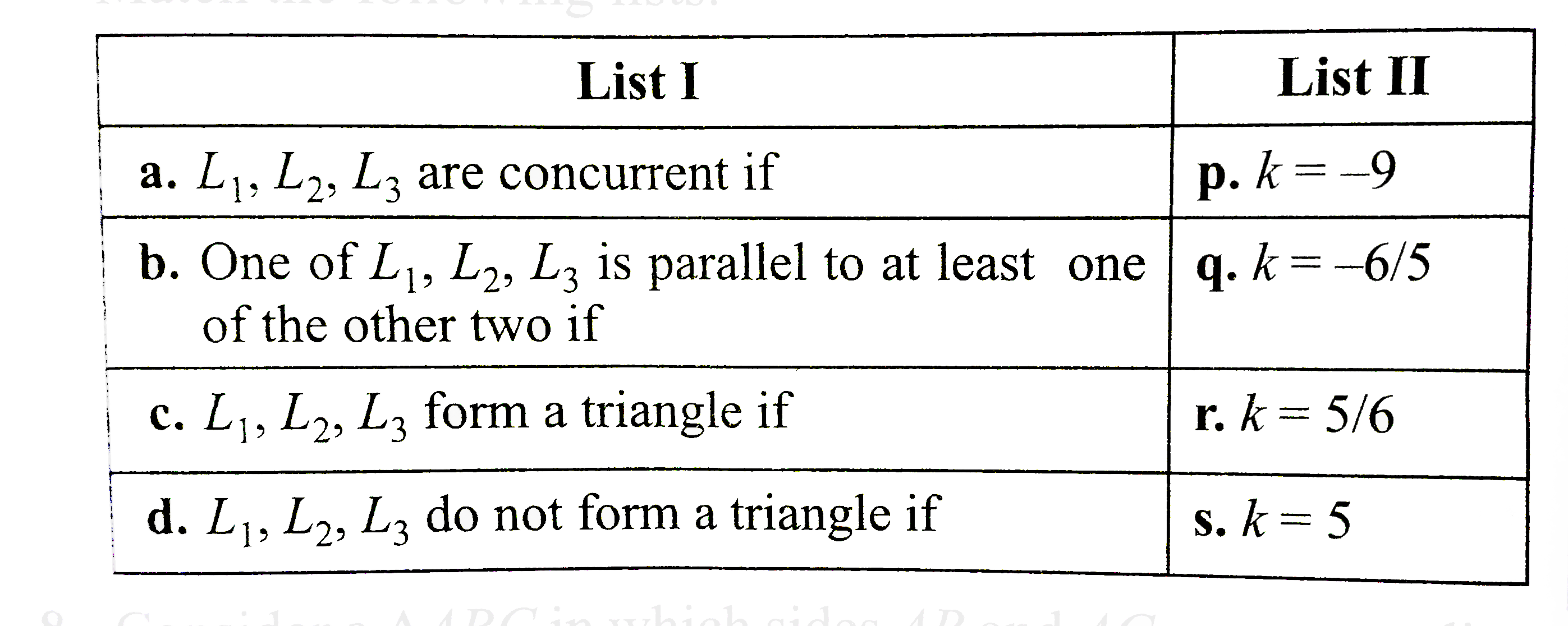
ocr_image

View Solution

Statement -1 : The lines (a + b) x + 2(a - b) y = 2a are concurrent at the point (1, 1/2) .
Statement-2 : $L_{1} + λ L_{2} = 0$ represents the equation of family of lines passing through the intersection of the lines $L_{1} = 0$ and $L_{2} = 0$ for all non - zero finite value of $λ$

View Solution

$θ_{1} and θ_{2}$ are the inclination of lines $L_{1} and L_{2}$ with the x-axis. If $L_{1} and L_{2}$ pass through $P (x_{1}, y_{1})$ , then the equation of one of the angle bisector of these lines is

View Solution

Let $C : y = x^{2} - 3, D : y = k x^{2}$ be two parabolas and
$L_{1}$ : $x = a, L_{2} : x = 1 (a \neq 0)$ be two straight lines.
IF the line $L_{1}$ meets the parabola C at a point B on the line $L_{2}$ , other than A, then a may be equal to

View Solution

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

ARIHANT MATHS ENGLISH-CIRCLE -Exercise (Passage Based Questions)