Two variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C is
x2+y2=a2
x2+y2=2a2
x2+y2=4a2
x2+y2=8a2
The correct Answer is:C
Step by step video & image solution for Two variable chords AB and BC of a circle x^(2)+y^(2)=a^(2) are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle. The locus of the points of intersection of tangents at A and C is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLE Book:ARIHANT MATHS ENGLISHChapter:CIRCLE Exercise:Exercise (Single Integer Answer Type Questions)
Explore 9 Videos
- CIRCLE Book:ARIHANT MATHS ENGLISHChapter:CIRCLE Exercise:Exercise (Statement I And Ii Type Questions)
Explore 7 Videos
- CIRCLE Book:ARIHANT MATHS ENGLISHChapter:CIRCLE Exercise:Exercise (More Than One Correct Option Type Questions)
Explore 15 Videos
- BIONOMIAL THEOREMBook:ARIHANT MATHS ENGLISHChapter:BIONOMIAL THEOREMExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 21 Videos
- COMPLEX NUMBERSBook:ARIHANT MATHS ENGLISHChapter:COMPLEX NUMBERSExercise:Complex Number Exercise 8
Explore 2 Videos
Similar Questions
Two variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
∠OAB is
View SolutionTwo variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
View Solution
Knowledge Check
AB and CD are chords of the circle, and E and F are the midpoints of the chords, respectively. The line EF passes through the center O of the circle. IF EF=17. then what is radius of the circle?
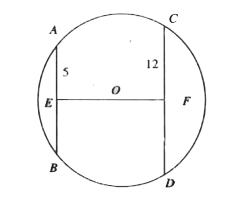 A10B12C13D15
A10B12C13D15
Two variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
View SolutionA chord AB of circle x2+y2=a2 touches the circle x2+y2−2ax=0.Locus of the point of intersection of tangens at A and B is :
View SolutionThe straight line x-2y+1=0 intersects the circle x2+y2=25 in points P and Q the coordinates of the point of intersection of tangents drawn at P and Q to the circle is
View SolutionThe straight line x−2y+5=0 intersects the circle x2+y2=25 in points P and Q, the coordinates of the point of the intersection of tangents drawn at P and Q to the circle is
View SolutionIn the figure, O is the center of the circle and BO is the bisector of ∠ABC show that AB=BC
View SolutionAB and AC are two chords of a circle of radius r such that AB=2AC. If p and q are the distances of AB and AC from the centre Prove that 4q2=p2+3r2.
View SolutionM and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that :
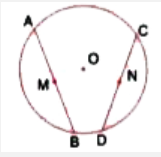
∠AMN=∠CNM.
View Solution
