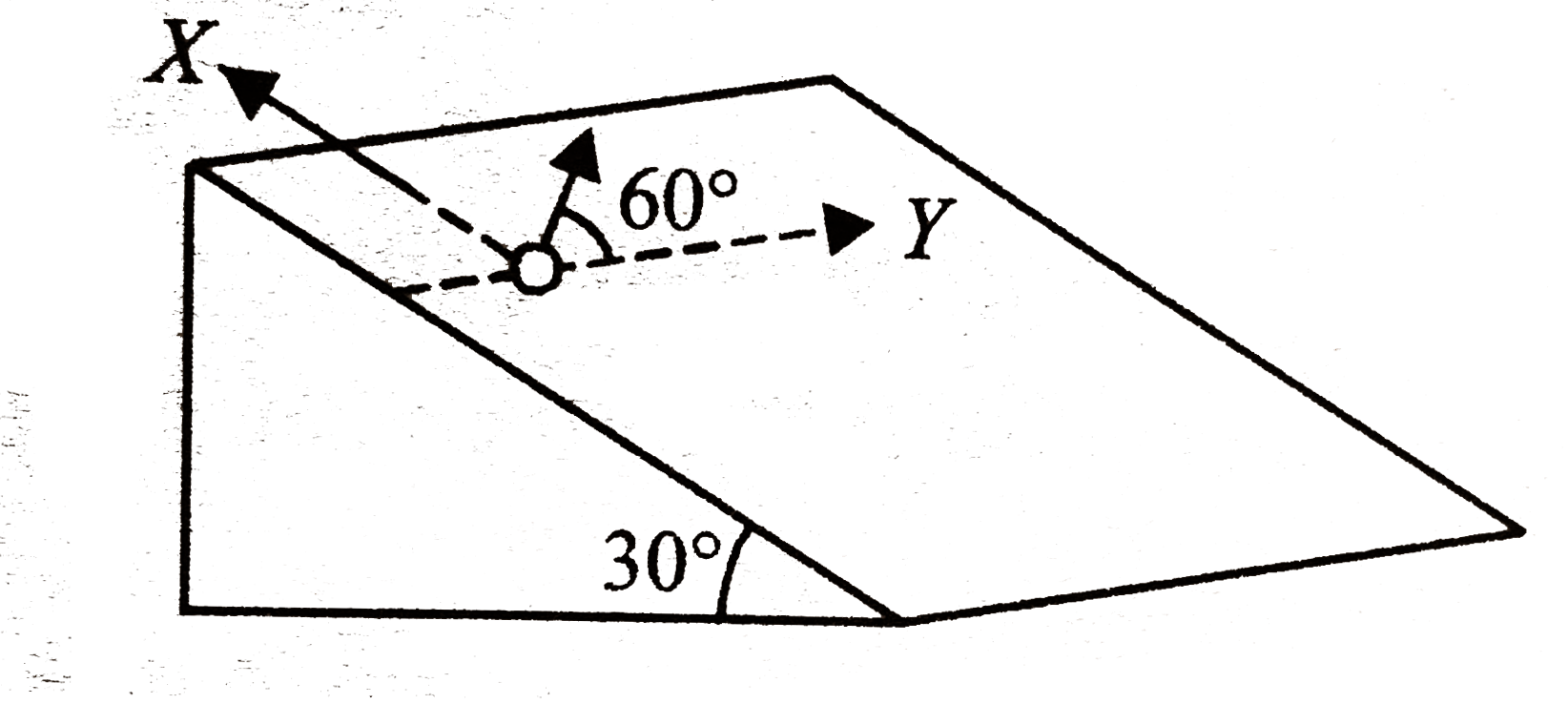
A small sphere is projected with a velocity of 3ms−1 in a direction 60∘ from the horizontal y - axis, on the smooth inclined plane (Fig. 5.197). The motion of sphere takes place in the x - y plane. Calculate the magnitude v of its velocity after 2s.
 .
.
The correct Answer is:1.5ms−1
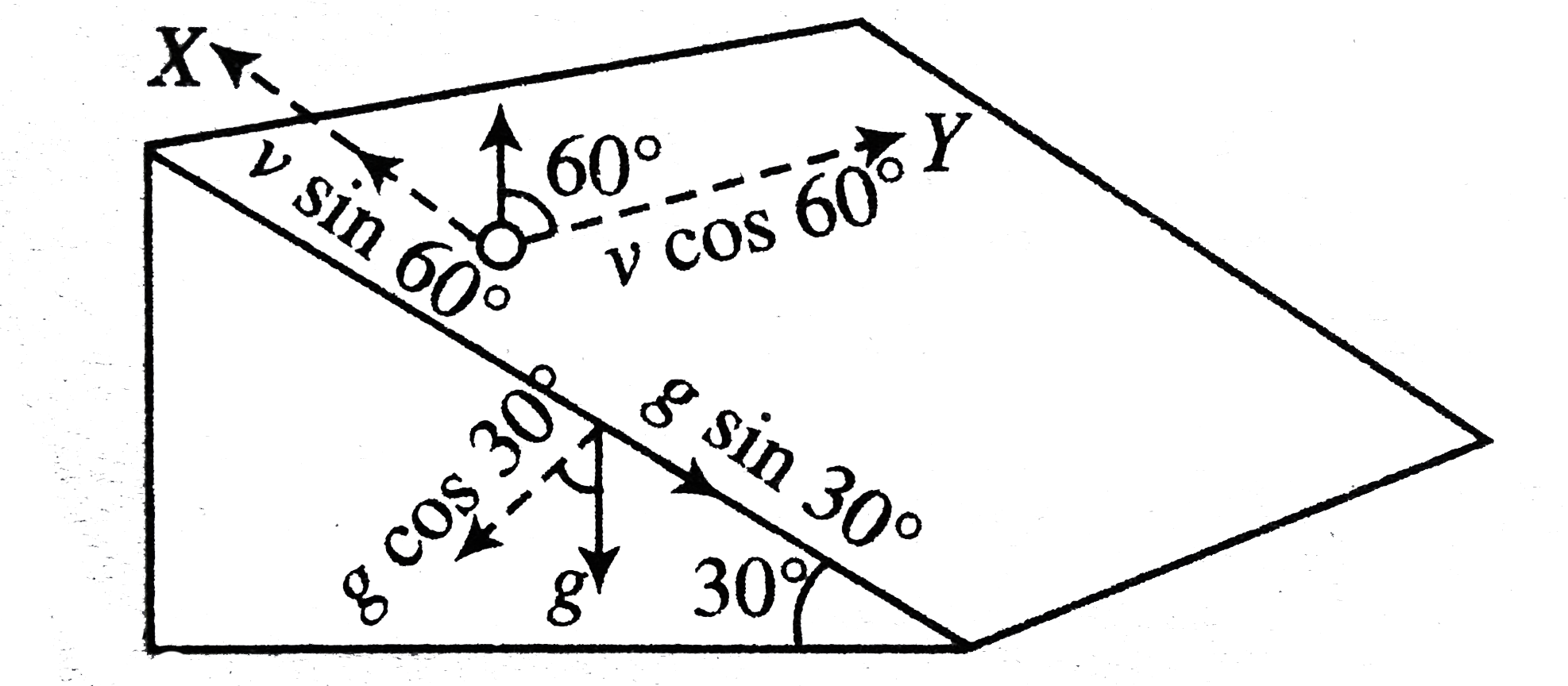
The motion of the sphere takes place in a plane , the x - and x - components of its acceleration are Ax=−gsin30∘, ay=0 The x- and y - components of the sphere's velocity at time t=2s are
Vx=v0x−axt=3sin60∘−gsin30∘×2=0.1ms−1
Vy=vcos60∘=constant=1.5ms−1
So the magnitude of sphere's velocity is
|→v|=√v2x+v2y=√(0.1)2+(1.5)2≅1.5ms−1
 .
.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct76videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct11videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.411videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
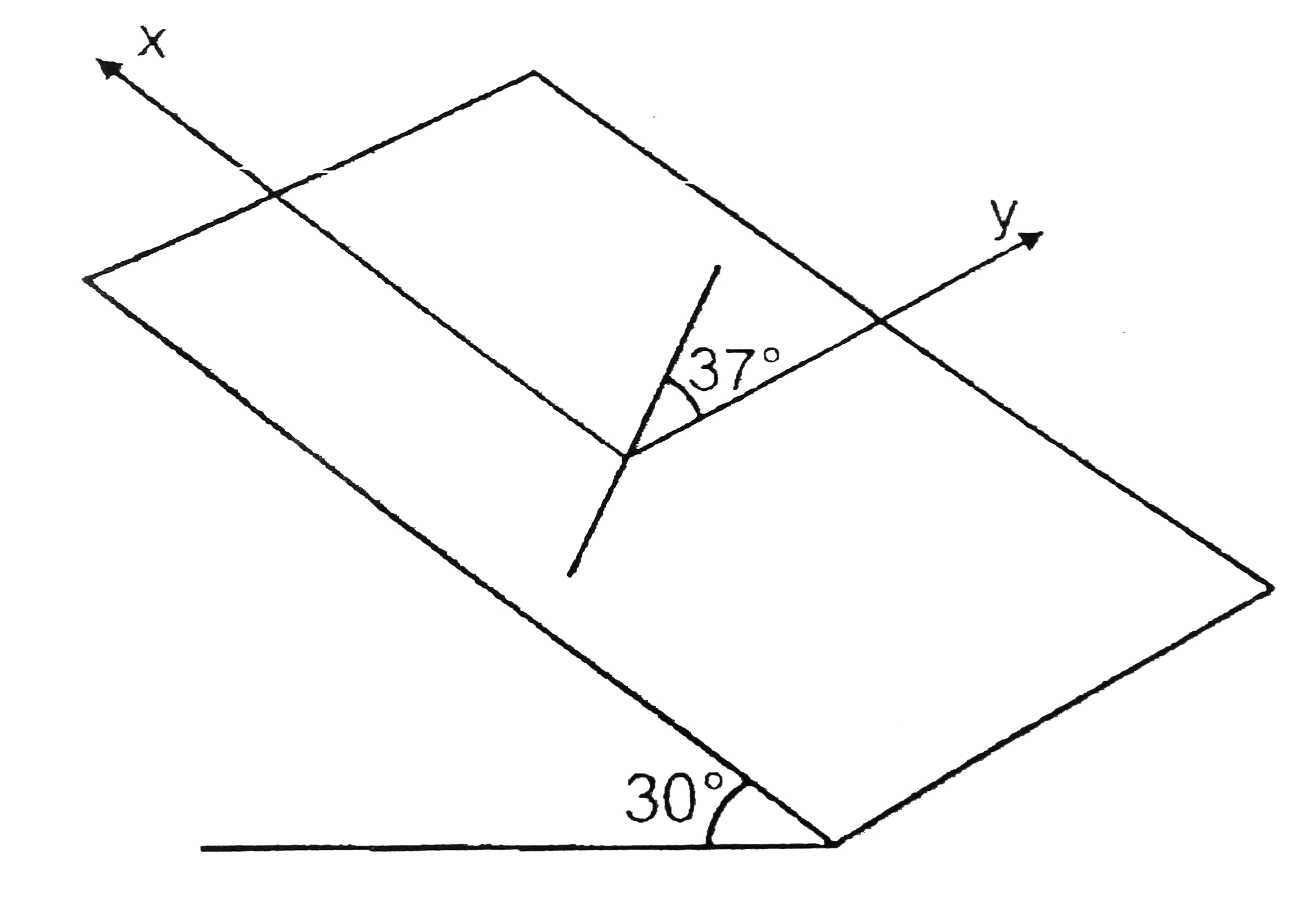
A small sphere is projected with velocity 5ms in a direction 37∘ from the horizontal y-axis on a smoother inclined plane. The motion of sphere takes plane in x-y plane. Magnitude of its velocity after 2 s is:View SolutionA body is projected with a velocity of 20ms−1 in a direction making an angle of 60∘ with the horizontal. Determine its (i) position after 0.5 s and (ii) the velocity after 0.5s.
View SolutionA particle is projected with a velocity of 20ms−1 at an angle of 60∘ to the horizontal. The particle hits the horizontal plane again during its journey. What will be the time of impact ?
View SolutionA body is projected with velocity 24 ms−1 making an angle 30° with the horizontal. The vertical component of its velocity after 2s is (g=10ms−1 )
View SolutionAn inclined plane makes an angle θ0=30∘ with the horizontal. A particle is projected from this plane with a speed of 5ms−1 at an angle of elevation β=30∘ with the horizontal as shown in (Fig. 5.53).
(a) Find the range of the particle on the plane when it strikes the plane.
(b) Find the range of the particle for β=120∘.
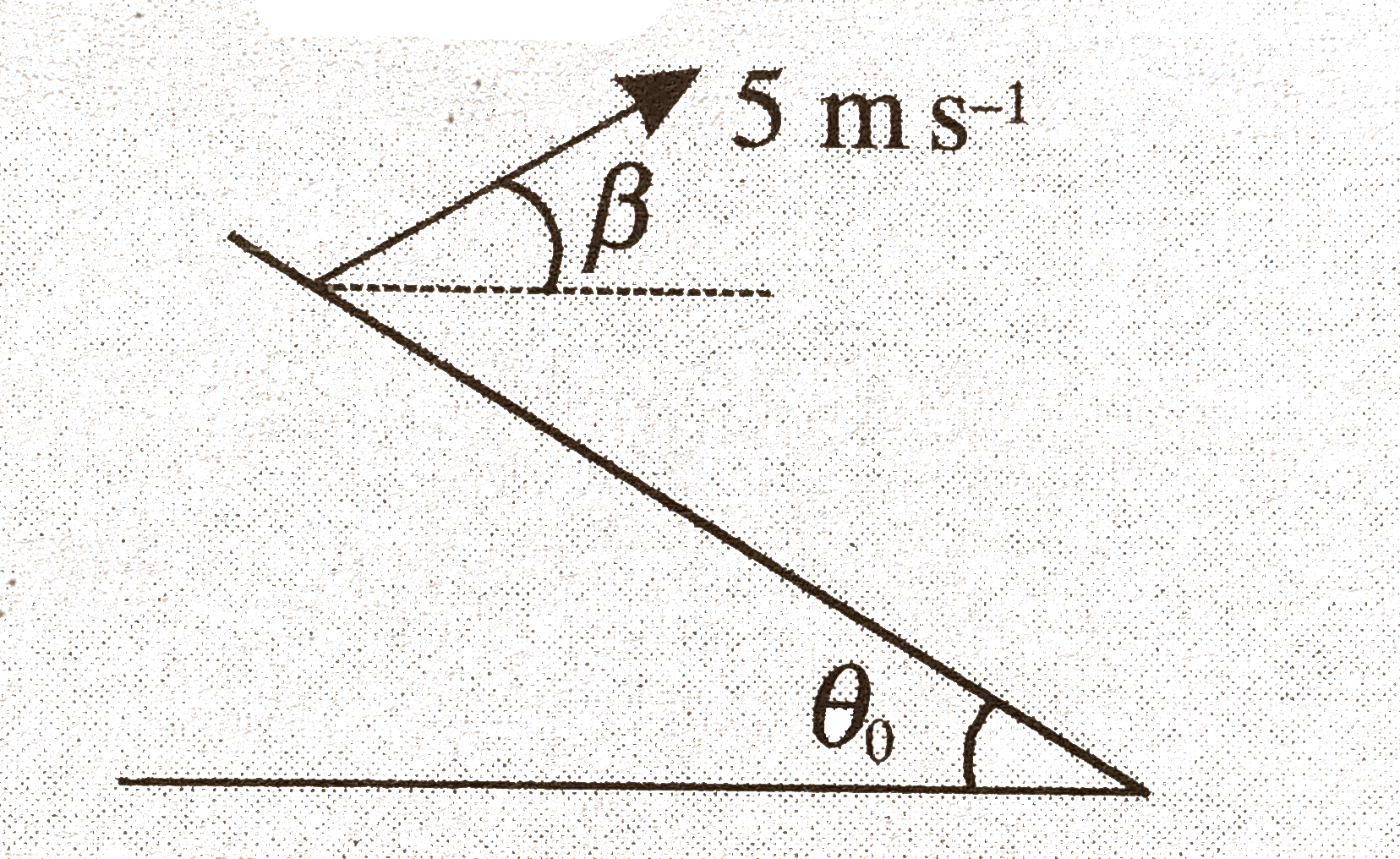 .View Solution
.View SolutionA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time
 View Solution
View SolutionA ball is projected with a velocity 20√3ms−1 at angle 60∘ to the horizontal. The time interval after which the velocity vector will make an angle 30∘ to the horizontal is (Take, g=10ms−2)
View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is
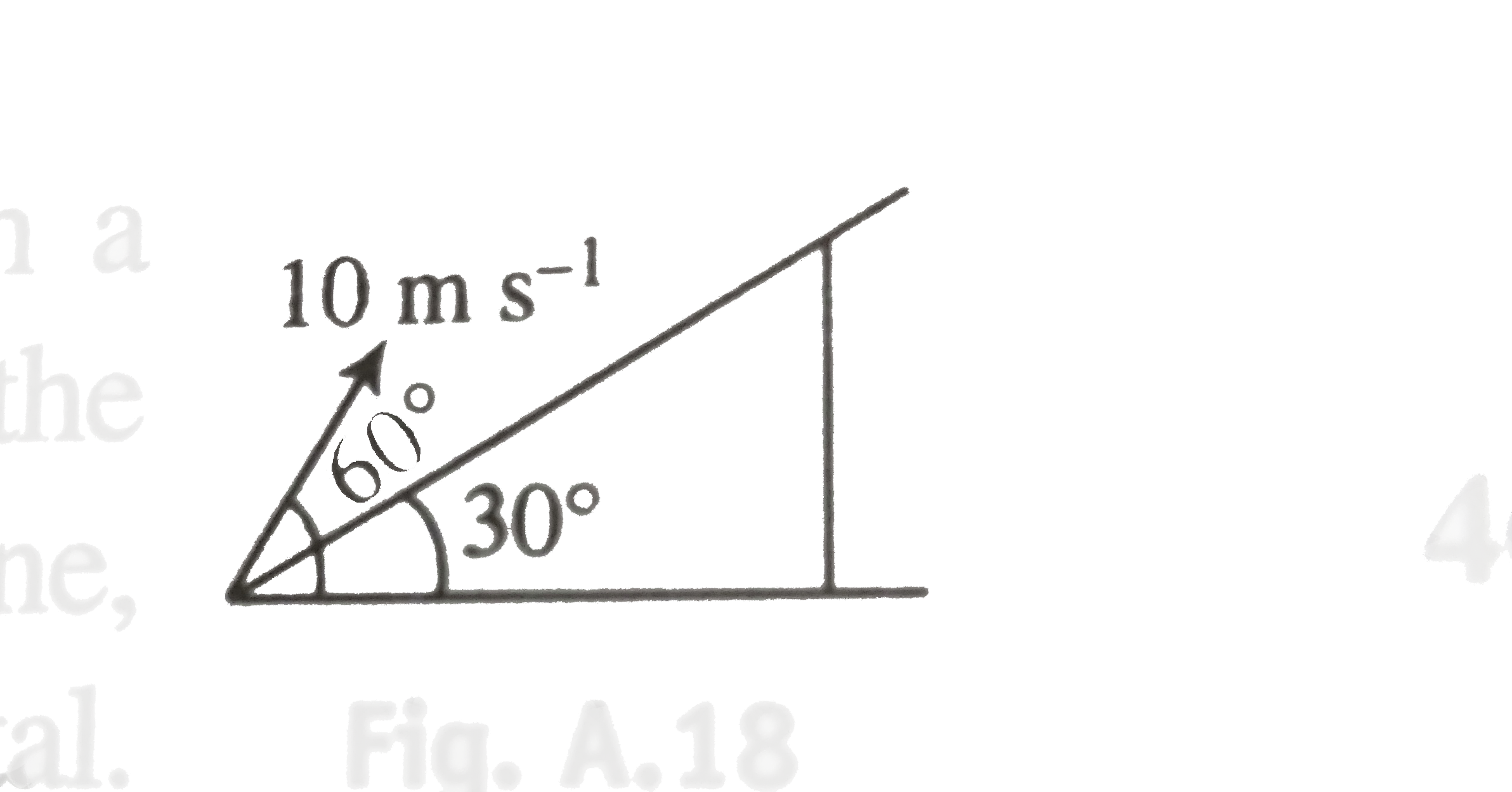 View Solution
View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is
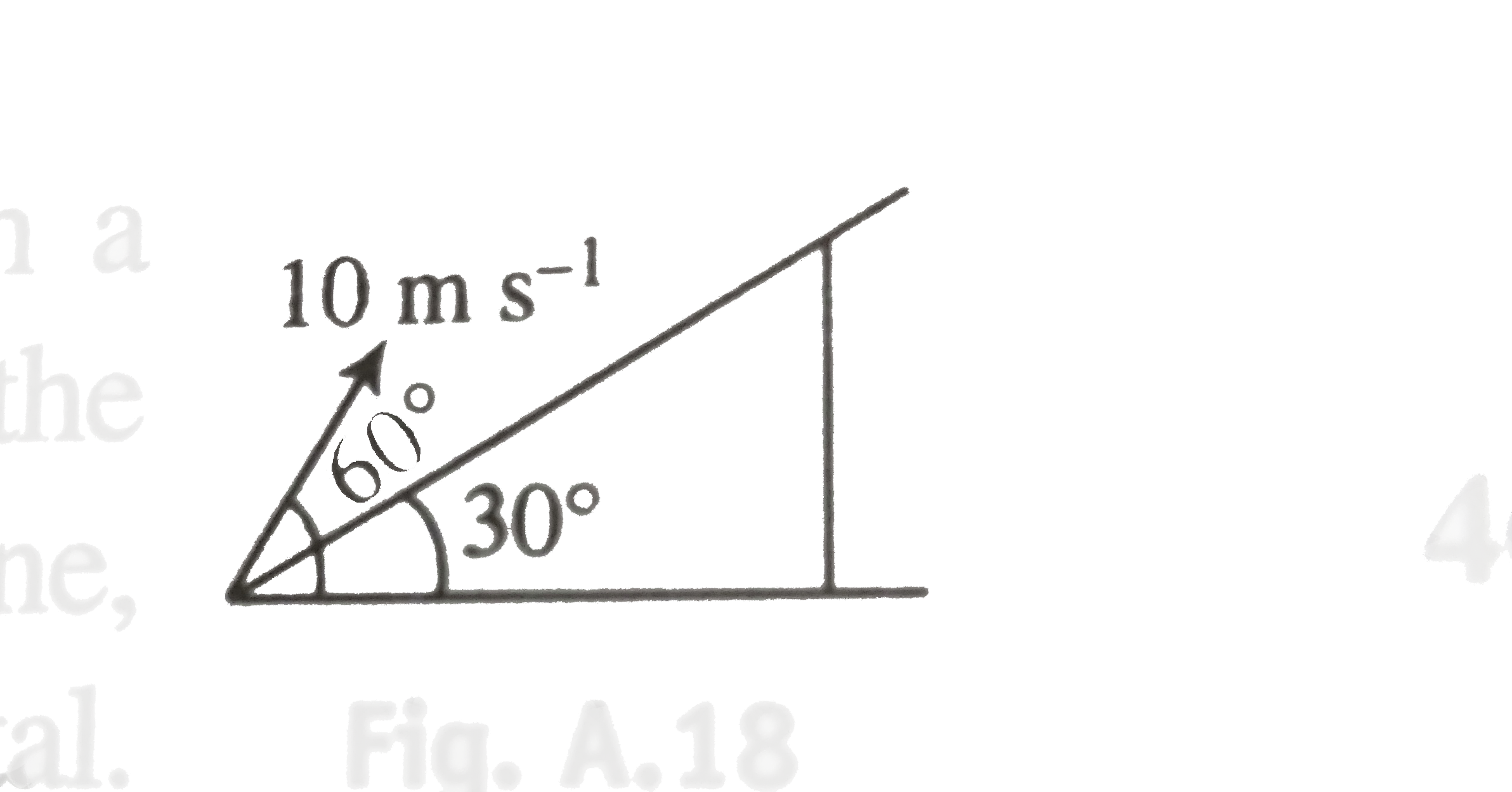 View Solution
View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is
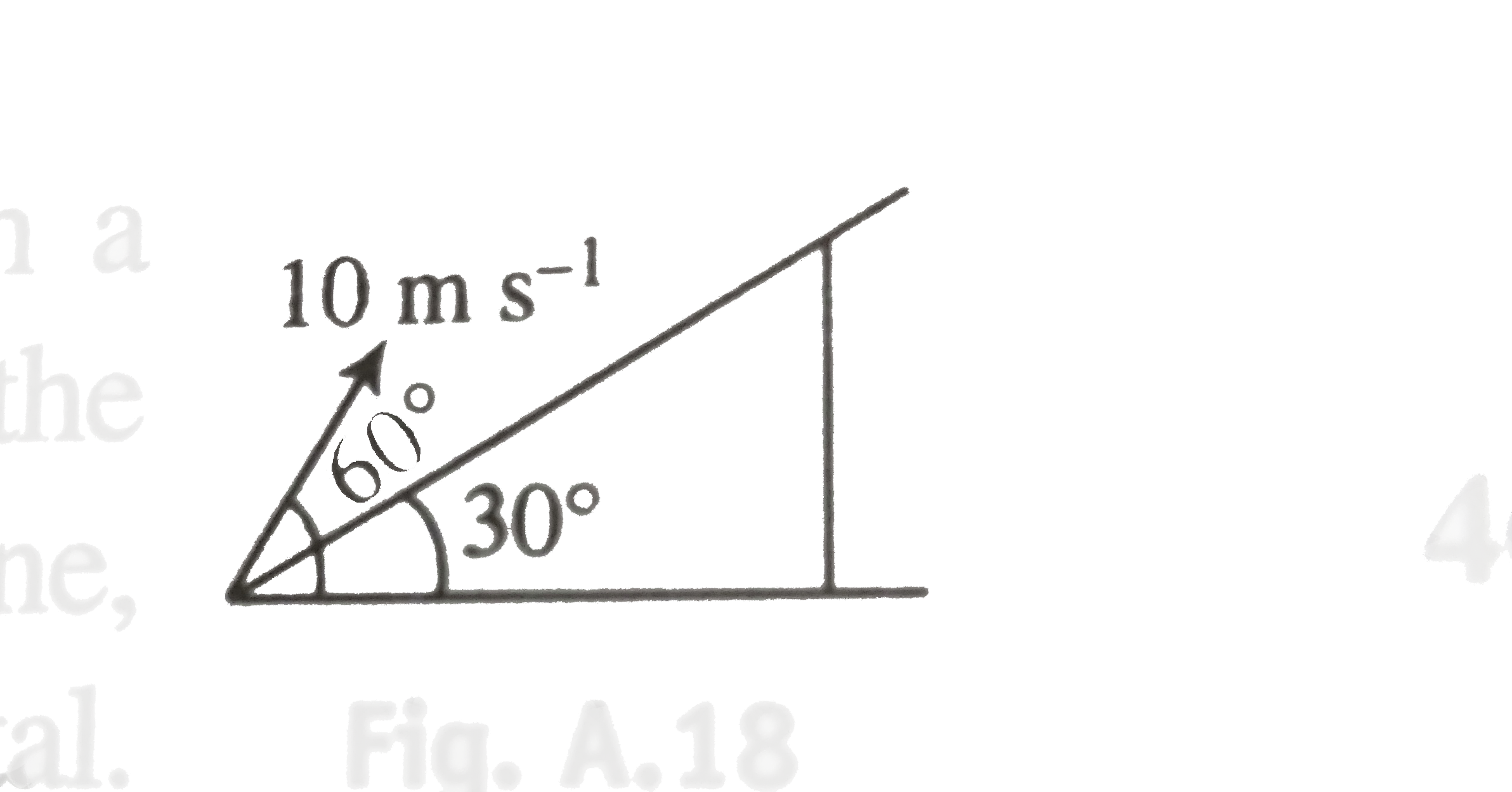 View Solution
View Solution

