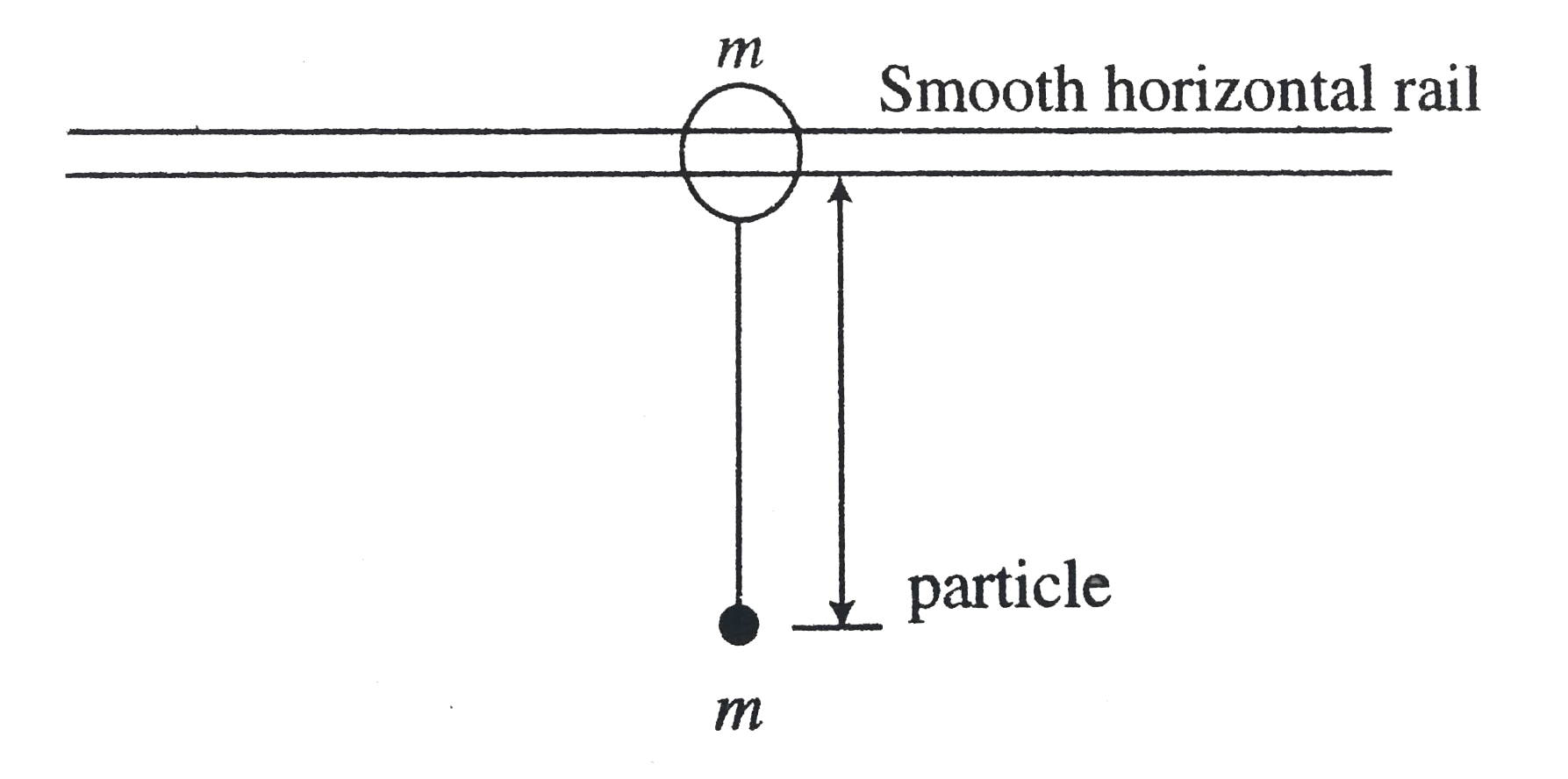
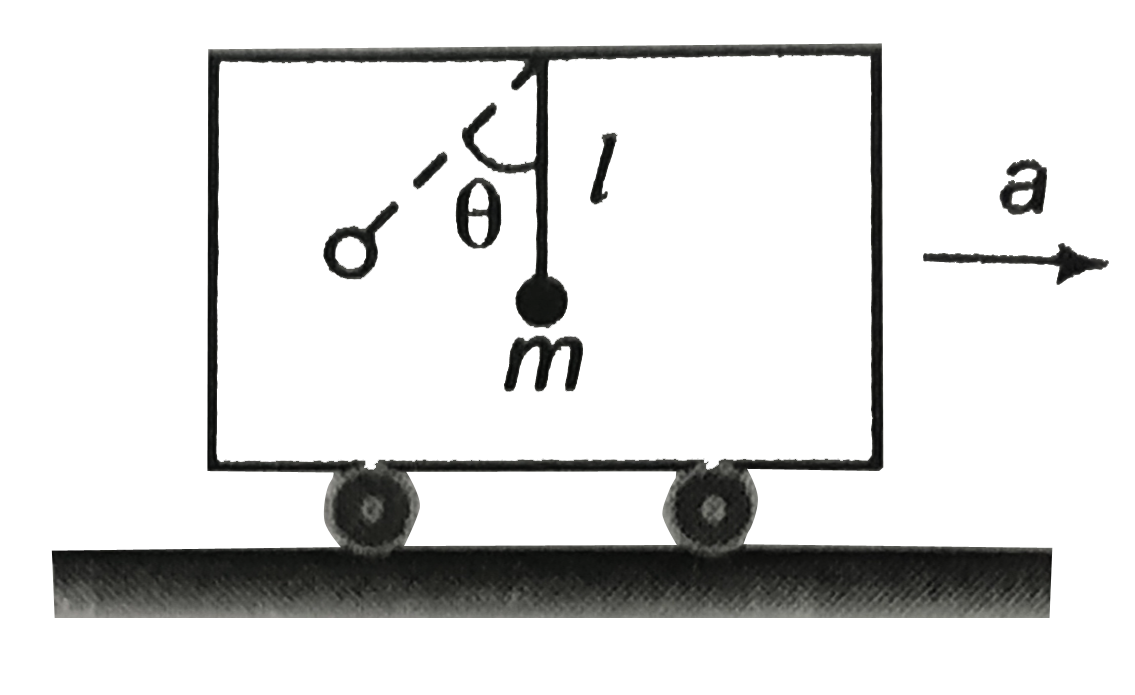
The ring shown in fig. is given a constant horizontal acceleration (a0=g√3). The maximum deflection of the string from the vertical is θ0. Then
a. θ0=30∘
b. θ0=60∘
c. At maximum deflection, tension in string is equal to mg.
d. At maximum deflection, tension in string is equal to 2mg√3
The correct Answer is:A, D
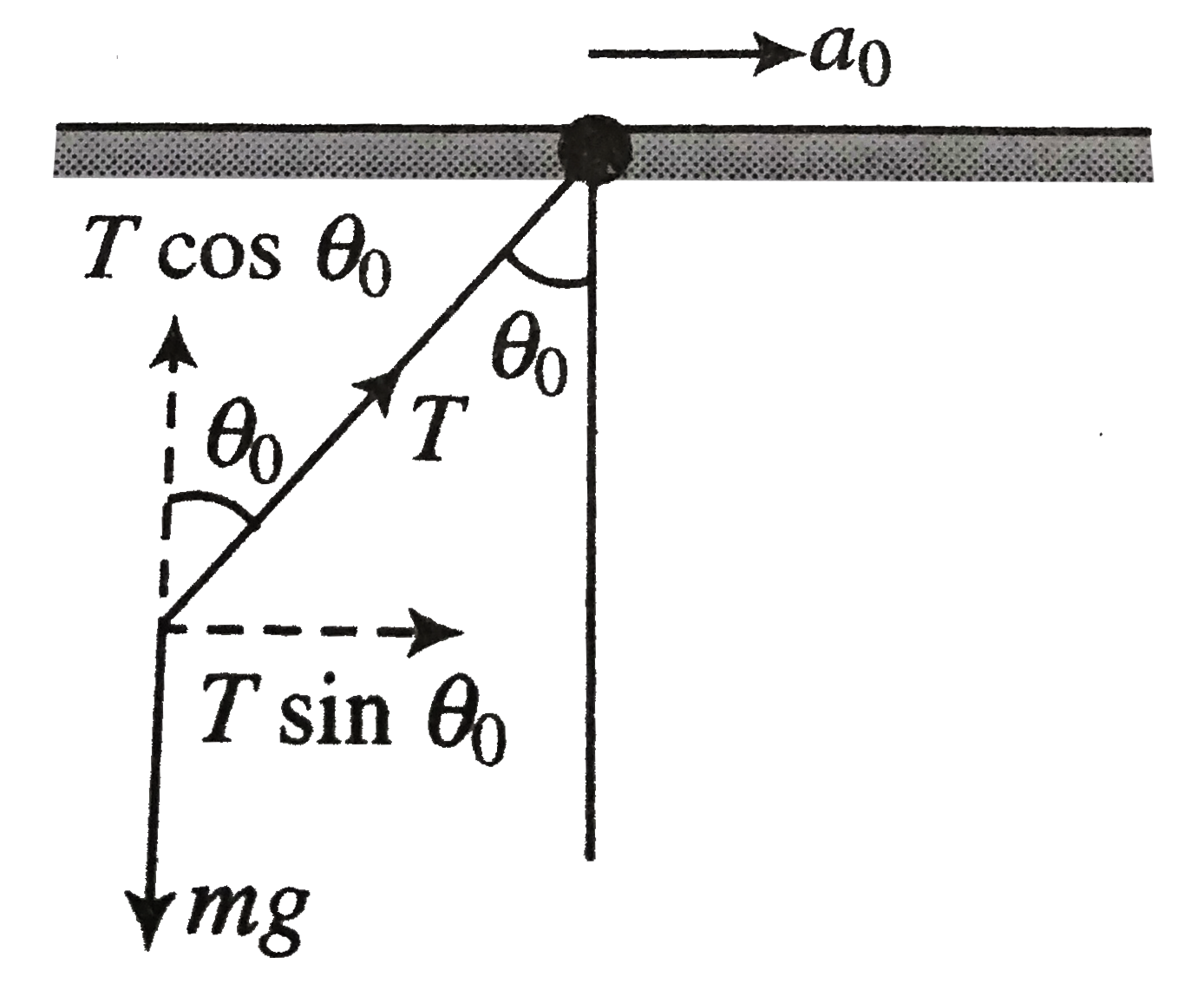
Tcosθ0=mg ..(i)
Tsinθ0=ma0 …(ii)
Dividing Eq, (ii) by (i) we get
tanθ0=ag⇒θ0=30∘ ltbtgt T=mgcos30∘=2mg√3
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning
15 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Linked Comperhension
46 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Single Correct
75 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Video
Similar Questions
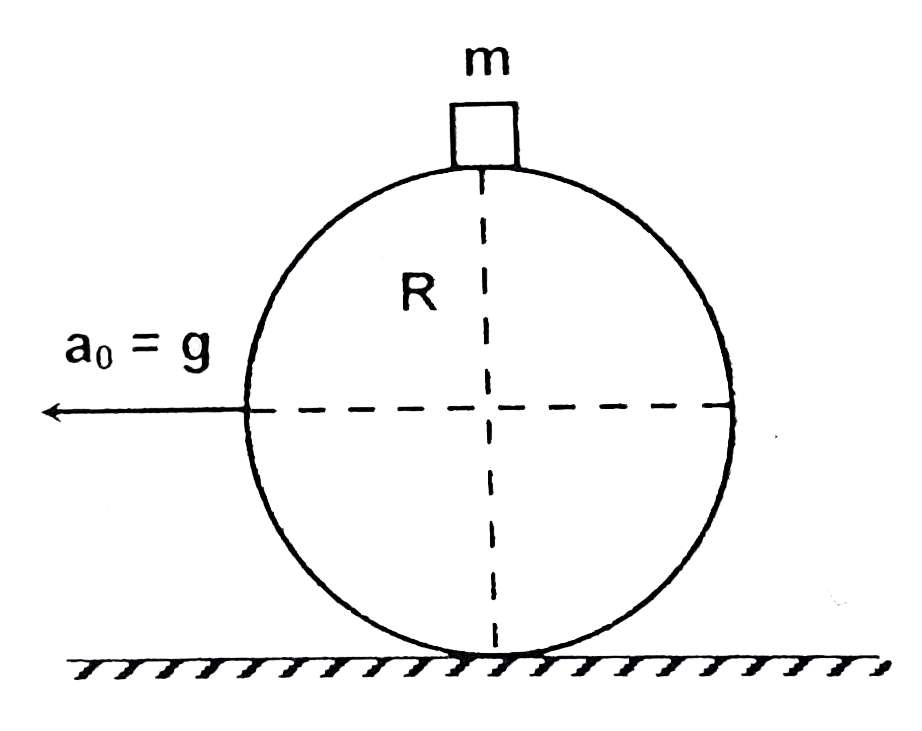
A small body of mass 'm' is placed at the top of a smooth sphere of radius 'R' placed on a horizontal surface as shown, Now the sphere is given a constant horizontal acceleration a0=g. The velocity of the body relative to the sphere at the moment when it loses contact with the sphere is
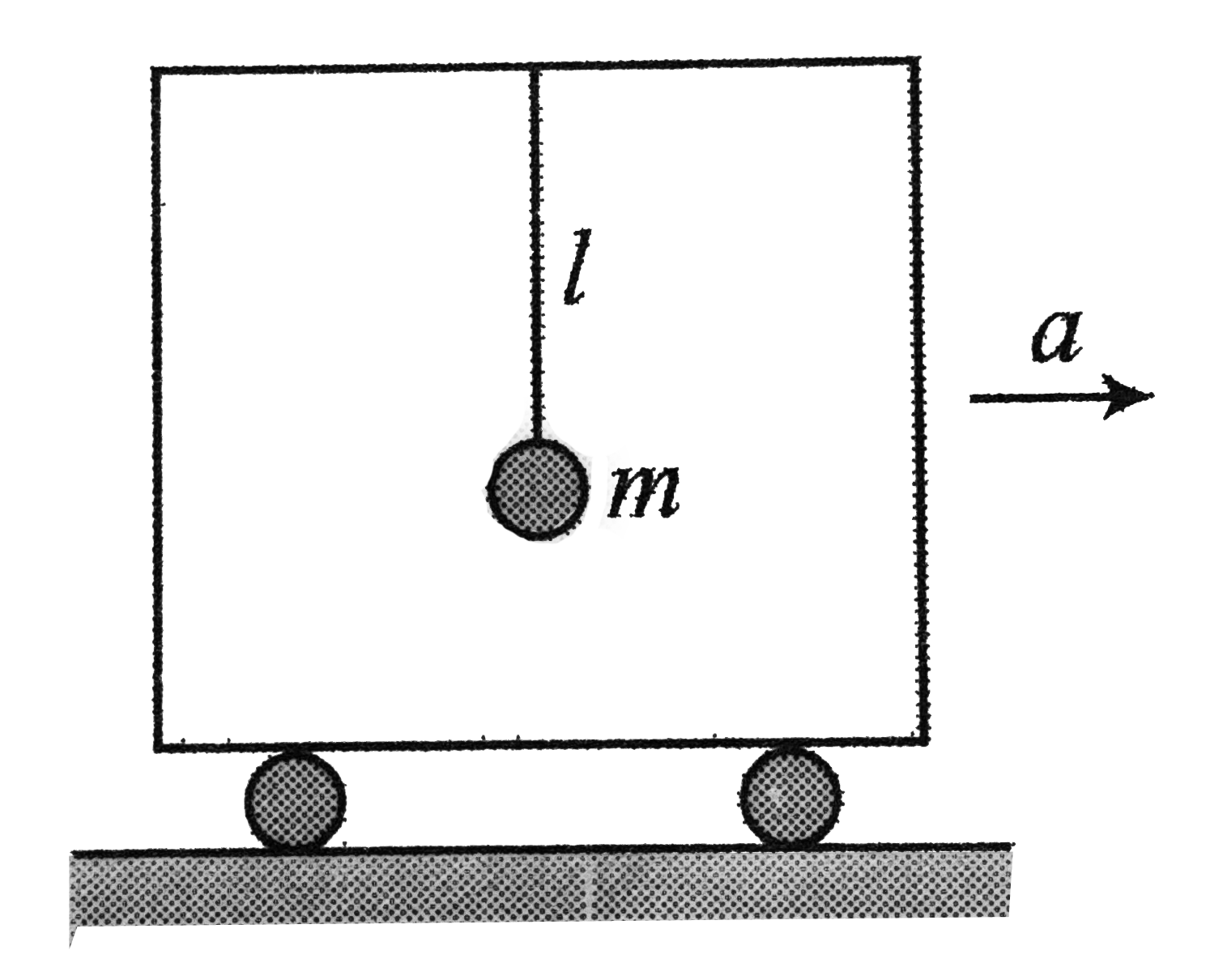
View SolutionA pendulum of mass m and length l is suspended from the ceiling of a trolley which has a constant acceleration a in the maximum deflection θ of the pendulum from the vertical.
View SolutionWhen the trolley show in figure is given a horizontal acceleration a, the pendulem bob of mass m gets deflected to a maximum deflection , the net acceleration of the bob with respect to trolley is
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
The maximum value of water pressure in the box is equal to
View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
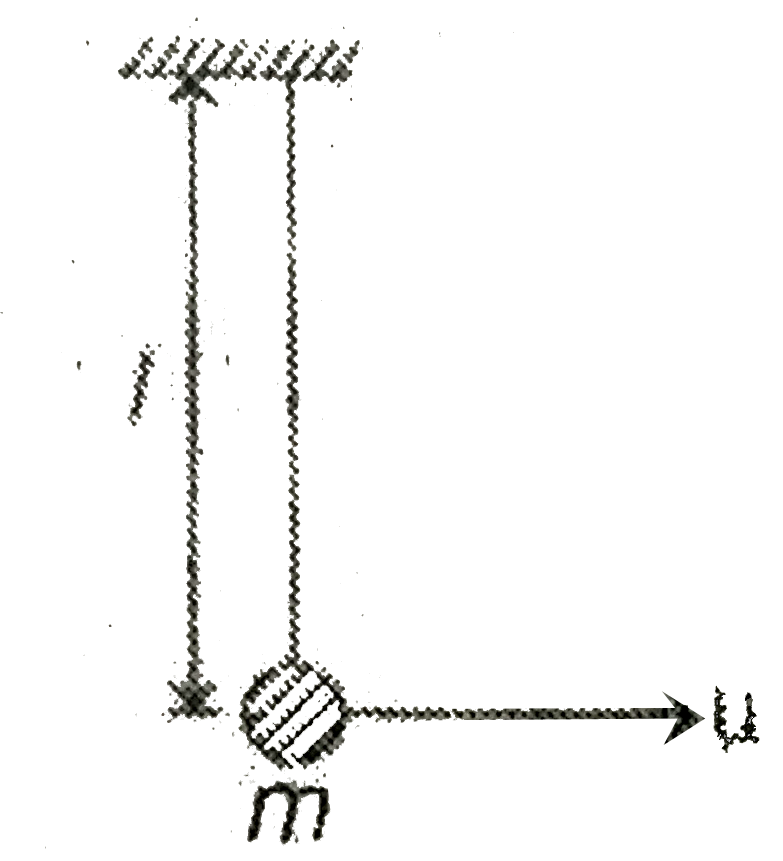
The maximum angle made by the string with downward vertical is
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
The angle of the free surface with the horizons is equal to
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
What is the value of vertical acceleration of box for given horizontal acceleration (g/2), so that no part of the bottom of the box is exposed?
View SolutionA small sphere is suspended by a string from the ceiling of a car. If the car beings to move with a constant acceleration a, the inclination of the string to the vertical is:
View Solution
Four identical metal butterflies are hanging from a light string of length 5l at equally placed points as shown. The ends of the string are attached to horizontal fixed support. The middle section of the string is horizontal . The relation between the angle θ1 and θ2 is given by
View SolutionA block of mass 1 kg and density 0.8g/cm3 is held stationary with the help of a string as shown in figure. The tank is accelerating vertically upwards with an acceleration a =1.0m/s2. Find

(a) the tension in the string,
(b) if the string is now cut find the acceleration of block.
(Take g=10m/s2 and density of water =103kg/m3).
View Solution
