A body has mass M and radius 2r. If the body assumes four shapes, solid cylinder, solid sphere, disc and ring of same radius, then the moment of inertia will be maximum about axis through centre of mass for:
ring
solid sphere
disc
solid cylinder
The correct Answer is:A
To solve the problem of finding which shape has the maximum moment of inertia about an axis through the center of mass, we will calculate the moment of inertia for each of the four shapes given: solid cylinder, solid sphere, disc, and ring.
1. Identify the Shapes and Their Formulas:
- We have four shapes: solid cylinder, solid sphere, disc, and ring.
- The formulas for the moment of inertia (I) for each shape about an axis through the center of mass are:
- Solid Cylinder: I=12MR2
- Solid Sphere: I=25MR2
- Disc: I=12MR2
- Ring: I=MR2
2. Substitute the Given Values:
- The mass of the body is M and the radius is 2r.
- We will substitute R=2r into each formula.
3. Calculate Moment of Inertia for Each Shape:
- Solid Cylinder:
Icylinder=12M(2r)2=12M(4r2)=2Mr2
- Solid Sphere:
Isphere=25M(2r)2=25M(4r2)=85Mr2
- Disc:
Idisc=12M(2r)2=12M(4r2)=2Mr2
- Ring:
Iring=M(2r)2=M(4r2)=4Mr2
4. Compare the Moments of Inertia:
- Now we have the moments of inertia for each shape:
- Solid Cylinder: 2Mr2
- Solid Sphere: 85Mr2 (which is 1.6Mr2)
- Disc: 2Mr2
- Ring: 4Mr2
5. Determine the Maximum Moment of Inertia:
- Comparing the values:
- 2Mr2 (Solid Cylinder)
- 1.6Mr2 (Solid Sphere)
- 2Mr2 (Disc)
- 4Mr2 (Ring)
- The maximum moment of inertia is 4Mr2 for the ring.
Conclusion:
The moment of inertia will be maximum about the axis through the center of mass for the ring.
---
- We have four shapes: solid cylinder, solid sphere, disc, and ring.
- The formulas for the moment of inertia (I) for each shape about an axis through the center of mass are:
- Solid Cylinder: I=12MR2
- Solid Sphere: I=25MR2
- Disc: I=12MR2
- Ring: I=MR2
- The mass of the body is M and the radius is 2r.
- We will substitute R=2r into each formula.
- Solid Cylinder:
Icylinder=12M(2r)2=12M(4r2)=2Mr2
Isphere=25M(2r)2=25M(4r2)=85Mr2
Idisc=12M(2r)2=12M(4r2)=2Mr2
Iring=M(2r)2=M(4r2)=4Mr2
- Now we have the moments of inertia for each shape:
- Solid Cylinder: 2Mr2
- Solid Sphere: 85Mr2 (which is 1.6Mr2)
- Disc: 2Mr2
- Ring: 4Mr2
- Comparing the values:
- 2Mr2 (Solid Cylinder)
- 1.6Mr2 (Solid Sphere)
- 2Mr2 (Disc)
- 4Mr2 (Ring)
- The maximum moment of inertia is 4Mr2 for the ring.
The moment of inertia will be maximum about the axis through the center of mass for the ring.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ENABLE
50 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EFFICIENT
50 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
Similar Questions
A solid cylinder of mass 20kg has length 1 m and radius 0.2 m. Then its moment of inertia (in kg-m2) about its geometrical axis is :
View SolutionThe mass of a body cannot be considered to be concentrated at the centre of mass of the body for the purpose of computing its moment of inertia.
For then the moment of inertia of every body about an axis passing through its centre of mass would be zero.
View SolutionA uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionThe mass of the cylinder is 25 kg and radius of cylinder is 5 m. Find the moment of inertia of a solid cylinder about a tangent to the cylinder.
View SolutionA disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
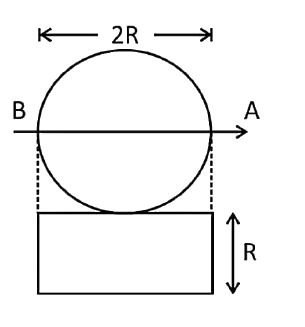
View SolutionA disc of mass m and radius R is attached to a rectangular plate of the same mass m, breadth R and length 2R as shown in figure. The moment of inertia of the system about the axis AB passing through the centre of the disc and along the plane is I=1α(313mR2).
View SolutionTwo spheres each of mass M and radius R/2 are connected with a massless rod of length R. Find the moment of inertia of the system about an axis passing through the centre of one of the sphere and perpendicular to the rod
View SolutionA disc of mass m and radius R has a concentric hole of radius r. Its moment of inertia about an axis through its center and perpendicular to its plane is
View SolutionWhy does a solid sphere have smaller moment of inertia than a hollow cylinder of same mass and radius, about an axis passing through their axes of symmentry ?
View Solution
