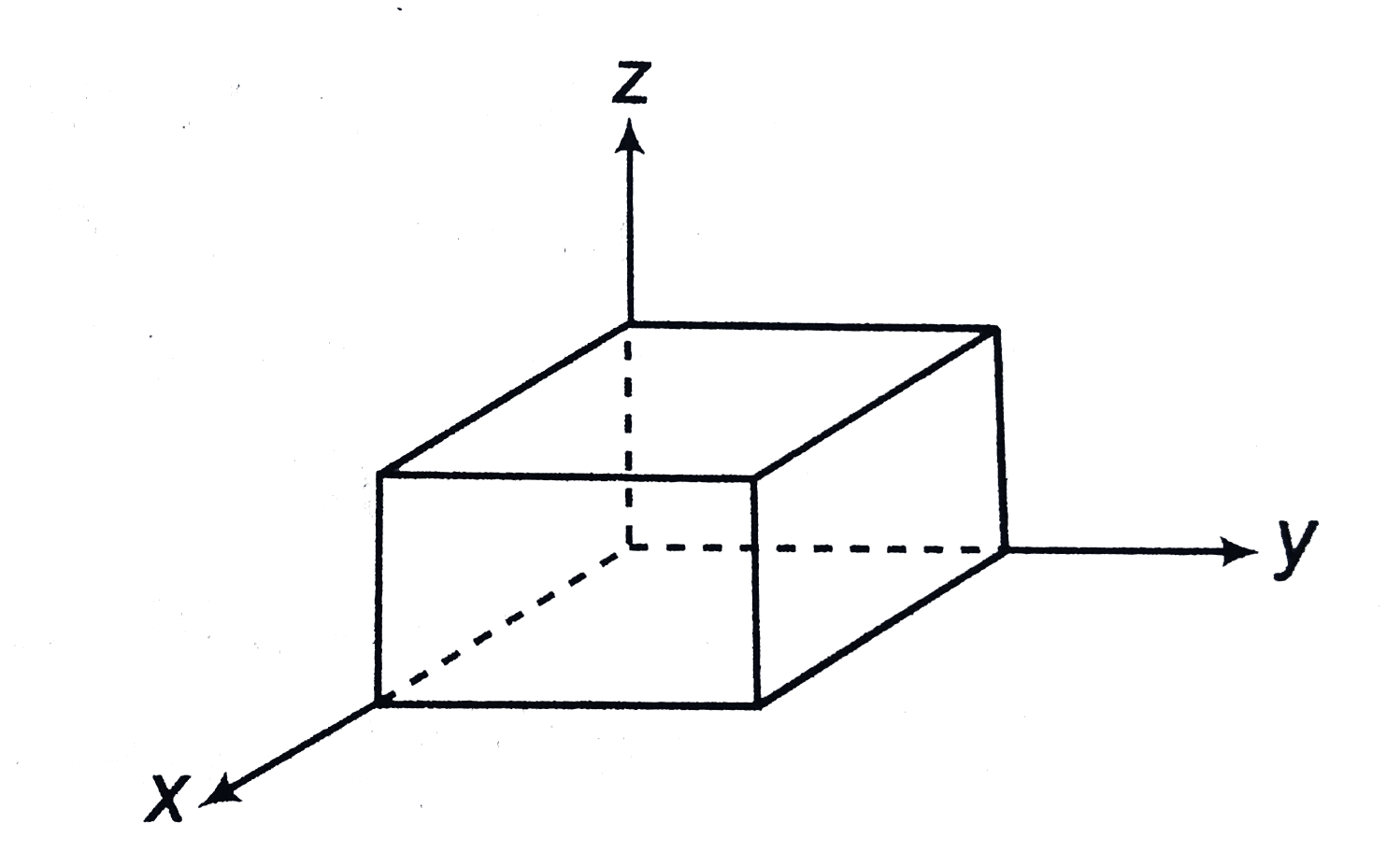
A cube has sides of length L=0.300m. It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by →E=(−5.00NC−1)xˆi+(3.00NC−1)zˆk.
The total electric charge inside the cube is
−0.054ε0C
0.081ε0C
0.135ε0C
0.054ε0C
The correct Answer is:A
To find the total electric charge inside the cube given the electric field, we can use Gauss's law, which states:
ΦE=Qencϵ0
where ΦE is the electric flux through a closed surface, Qenc is the total charge enclosed by the surface, and ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2.
Step 1: Calculate the Electric Flux through Each Face of the Cube
The electric field is given by:
→E=(−5.00N/C)^i+(3.00N/C)^k
The cube has 6 faces, and we need to calculate the electric flux through each face.
Face 1 (x = 0):
- Area vector →A1=L2^i
- Φ1=→E⋅→A1=(−5.00)⋅(0.32)=−0.45N m2/C
Face 2 (x = L):
- Area vector →A2=−L2^i
- Φ2=→E⋅→A2=(−5.00)⋅(0.32)=−0.45N m2/C
Face 3 (y = 0):
- Area vector →A3=L2^j
- Φ3=→E⋅→A3=0 (since ^j is perpendicular to →E)
Face 4 (y = L):
- Area vector →A4=−L2^j
- Φ4=→E⋅→A4=0
Face 5 (z = 0):
- Area vector →A5=L2^k
- Φ5=→E⋅→A5=(3.00)⋅(0.32)=0.27N m2/C
Face 6 (z = L):
- Area vector →A6=−L2^k
- Φ6=→E⋅→A6=(3.00)⋅(0.32)=0.27N m2/C
Step 2: Sum the Electric Flux
Now, we sum the flux through all the faces:
ΦE=Φ1+Φ2+Φ3+Φ4+Φ5+Φ6
ΦE=(−0.45)+(−0.45)+0+0+0.27+0.27=−0.36N m2/C
Step 3: Use Gauss's Law to Find the Charge
Using Gauss's law:
ΦE=Qencϵ0
Rearranging gives:
Qenc=ΦE⋅ϵ0
Substituting the values:
Qenc=−0.36⋅(8.85×10−12)=−3.19×10−12C
Final Answer
The total electric charge inside the cube is approximately:
Qenc≈−3.19pC
- Area vector →A1=L2^i
- Φ1=→E⋅→A1=(−5.00)⋅(0.32)=−0.45N m2/C
- Area vector →A2=−L2^i
- Φ2=→E⋅→A2=(−5.00)⋅(0.32)=−0.45N m2/C
- Area vector →A3=L2^j
- Φ3=→E⋅→A3=0 (since ^j is perpendicular to →E)
- Area vector →A4=−L2^j
- Φ4=→E⋅→A4=0
- Area vector →A5=L2^k
- Φ5=→E⋅→A5=(3.00)⋅(0.32)=0.27N m2/C
- Area vector →A6=−L2^k
- Φ6=→E⋅→A6=(3.00)⋅(0.32)=0.27N m2/C
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective type7videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct8videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.515videos
ELECTRIC POTENTIAL
Similar Questions
A cube has sides of length L=0.300m. It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by →E=(−5.00NC−1)xˆi+(3.00NC−1)zˆk.
The flux passing through the surface S5 will beView SolutionA cube has sides of length L. It is placed with one corner at the origin ( refer to Fig.2.119). The electric field is uniform and given by →€=−Bˆi+Cˆj−Dˆk , where B,C,andD are positive constants.
The total flux passing through the cube isView SolutionA cube has sides of length L=0.2m. It is placed with one corner at the origin as shown in figure. The electric field is uniform and given by E=(2.5N/C)ˆi−(4.2N/C)ˆj. Find the electric flux through the entire cube.
 View Solution
View SolutionA cube has sides of length L. It is placed with one corner at the origin as shown in figure. The electric field is uniform and given by E=−Bˆi+Cˆj−Dˆk, where B, C and D are positive constants.
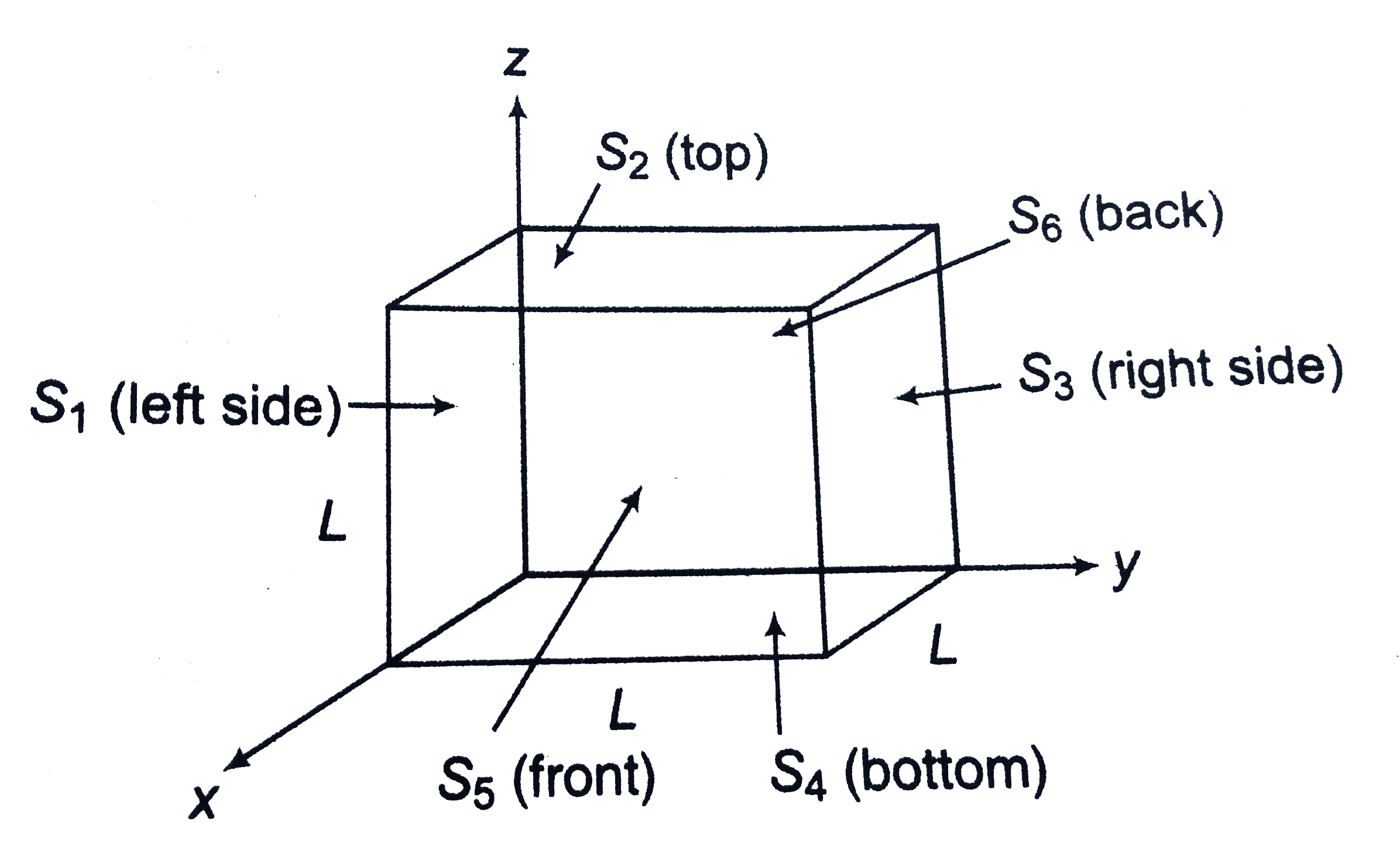
(a) Find the electric flux through each of the six cube faces S1,S2,S3,S4andS5andS6.
(b) Find the electric flux through the entire cube.View SolutionElectric field in a region is given by →E=−4xˆi+6yˆj. Then find the charge enclosed in the cube of side 1m oriented as shown in the diagram
 View Solution
View SolutionA cube of side a is placed in a uniform electric field E=E0ˆi+E0ˆj+E0k. Total electric flux passing through the cube would be
View SolutionA bollow cylindrical box of length 1m and area of cross section 25cm2 is placed in a three dimensional co-ordinate system as shown in Fig, The electric field in the
region is given by →E=50xˆi , where E is in NC−1 and x is in meter. Find
(i) Net flux through the cylinder
(ii) Charge enclosed by the cylinder.
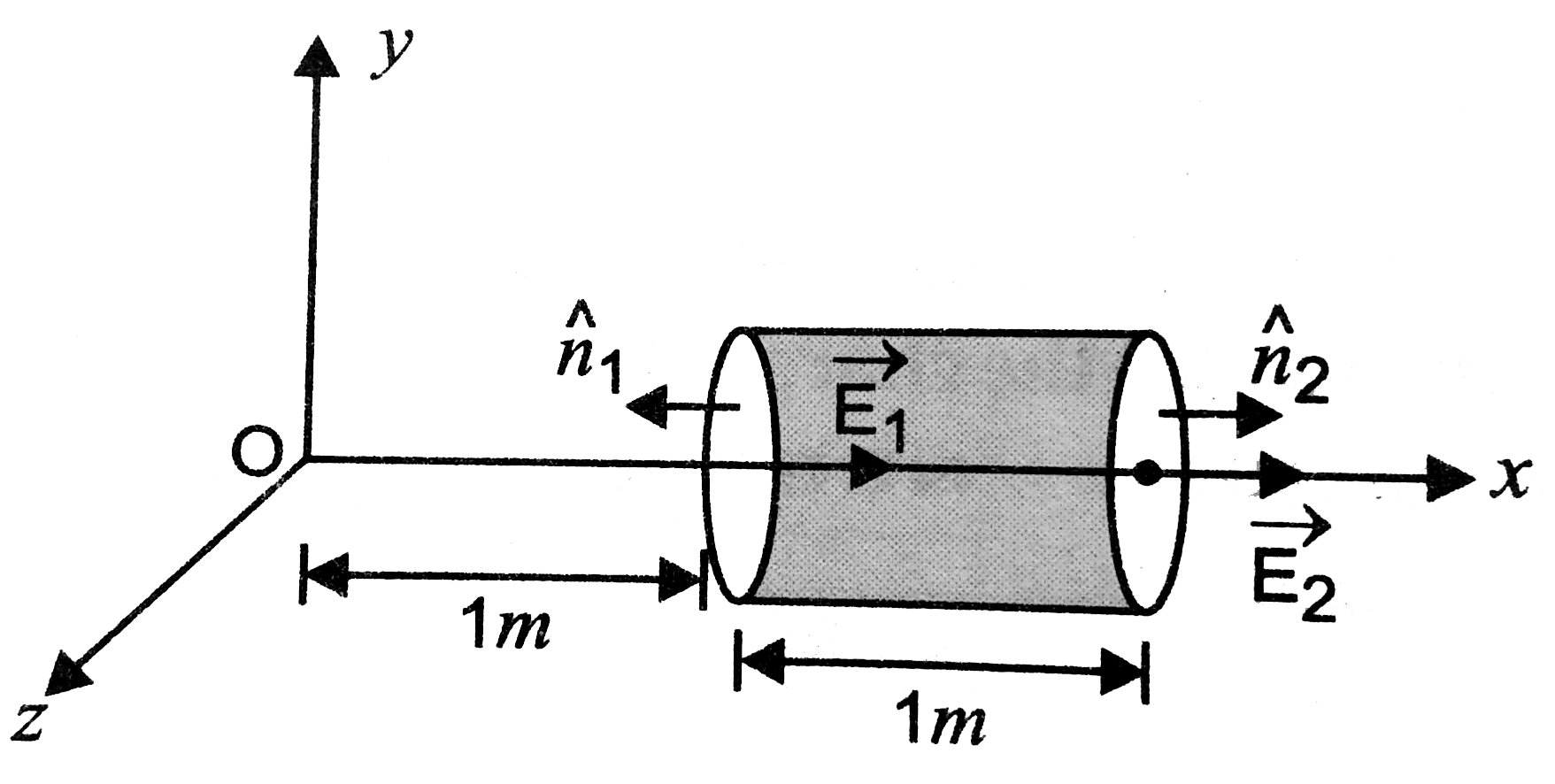 View Solution
View SolutionThe electric field ina region is given as
E=1ε0[(2y2+z)ˆi+4xyˆj+xˆk]V/m
Find volume charge density at ( - 1, 0,3) .View SolutionA hollow cylindrical box of length 0.5m and area of cross-section 20cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by →E=20xˆi, where E is NC−1 and x is in meters, Find

(i) Net flux through the cylinder.
(ii) Charge enclosed in the cylinder.View SolutionThe cube in figure has edge length √2m and is oriented as shown in a region of uniform electric field , in newtons per coulomb, is given by (a)6.00ˆi,(b)−2.00ˆj,and(c)−3.00ˆj+4.00ˆk . (d) what is the total flux through the cube for each field ?
 View Solution
View Solution

