Two wires made of tinned copper having identical cross section (=10−6m2) and lengths 10and15cm are to be used as fuses. Show that the fuses will melt at the same value of current in each case.
To show that the two wires made of tinned copper will melt at the same value of current, we can follow these steps:
Step 1: Understand the Heat Produced by the Current
The heat produced per second (power) in a wire due to the current can be expressed using the formula:
P=I2R
where P is the power (heat produced per second), I is the current, and R is the resistance of the wire.
Step 2: Calculate the Resistance of Each Wire
The resistance R of a wire can be calculated using the formula:
R=ρLA
where ρ is the resistivity of the material, L is the length of the wire, and A is the cross-sectional area.
Given:
- Cross-sectional area A=10−6m2
- Length of wire 1 L1=10cm=0.1m
- Length of wire 2 L2=15cm=0.15m
Calculating the resistance for each wire:
- For wire 1:
R1=ρ0.110−6=0.1ρ×106=105ρ
- For wire 2:
R2=ρ0.1510−6=0.15ρ×106=1.5×105ρ
Step 3: Set Up the Power Equations
Using the power formula for both wires:
- For wire 1:
P1=I2R1=I2(105ρ)
- For wire 2:
P2=I2R2=I2(1.5×105ρ)
Step 4: Determine the Melting Condition
The fuses will melt when the heat produced equals the heat lost. Since the heat loss is proportional to the surface area and the heat produced is proportional to the resistance, we can set the conditions for melting.
Step 5: Equate the Power for Melting
Since both wires are made of the same material (tinned copper) and have the same cross-sectional area, the melting condition can be equated:
I2(105ρ)=I2(1.5×105ρ)
Step 6: Conclusion
From the above equations, we can see that the current I will not affect the melting condition since the resistivity ρ and the cross-sectional area A are constant. Therefore, both wires will melt at the same current value because the ratio of their resistances will not affect the current needed to produce enough heat to reach the melting point.
Final Answer
Thus, we have shown that the fuses will melt at the same value of current in each case.
---
The heat produced per second (power) in a wire due to the current can be expressed using the formula:
P=I2R
where P is the power (heat produced per second), I is the current, and R is the resistance of the wire.
The resistance R of a wire can be calculated using the formula:
R=ρLA
where ρ is the resistivity of the material, L is the length of the wire, and A is the cross-sectional area.
- Cross-sectional area A=10−6m2
- Length of wire 1 L1=10cm=0.1m
- Length of wire 2 L2=15cm=0.15m
- For wire 1:
R1=ρ0.110−6=0.1ρ×106=105ρ
R2=ρ0.1510−6=0.15ρ×106=1.5×105ρ
Using the power formula for both wires:
- For wire 1:
P1=I2R1=I2(105ρ)
P2=I2R2=I2(1.5×105ρ)
The fuses will melt when the heat produced equals the heat lost. Since the heat loss is proportional to the surface area and the heat produced is proportional to the resistance, we can set the conditions for melting.
Since both wires are made of the same material (tinned copper) and have the same cross-sectional area, the melting condition can be equated:
I2(105ρ)=I2(1.5×105ρ)
From the above equations, we can see that the current I will not affect the melting condition since the resistivity ρ and the cross-sectional area A are constant. Therefore, both wires will melt at the same current value because the ratio of their resistances will not affect the current needed to produce enough heat to reach the melting point.
Thus, we have shown that the fuses will melt at the same value of current in each case.
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Solved Examples
13 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Exercise 7.1
22 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type
4 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
Similar Questions
Three rods made of the same material and having same cross-section area but different length 10 cm, 20 cm and 30 cm are joined as shown. The temperature of the junction is
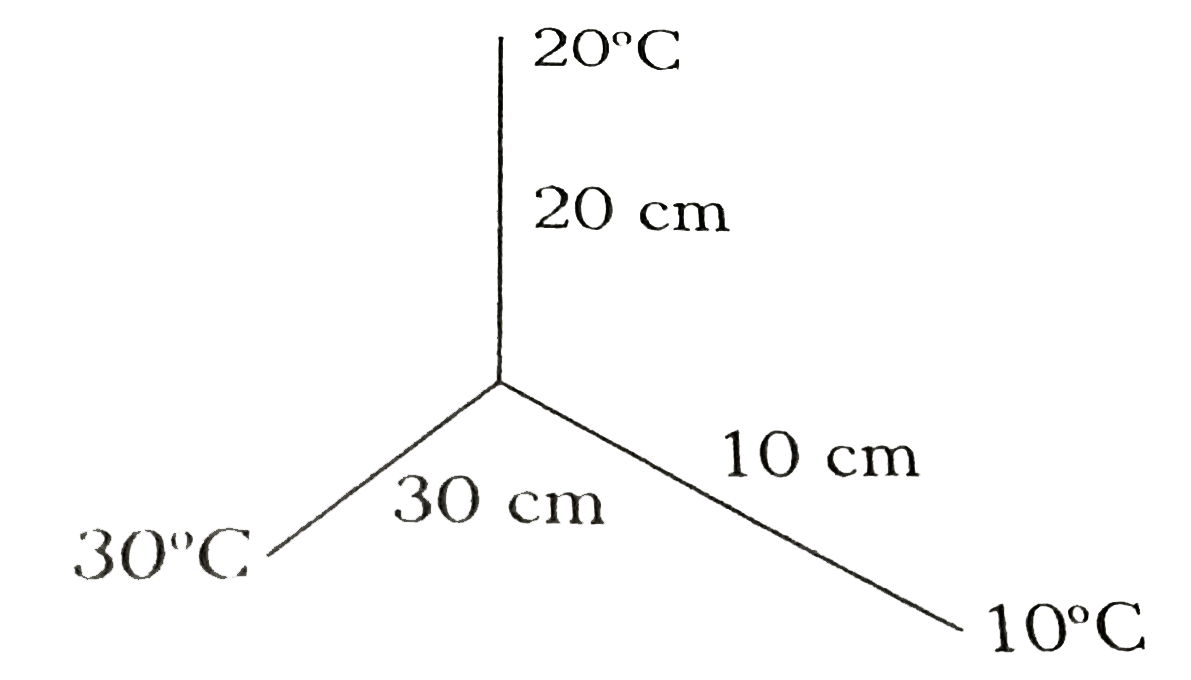
View SolutionTwo coaxial solenoids are made by winding thin insulated wire over a pipe of cross-sectional area A=10cm2 and length =10cm. If one of the solenoid has 300 turns and the other 400 turns, their mutual indcutance is
View Solution
Knowledge Check
The self inductance of a solenoid that has a cross-sectional area of 1cm2, a length of 10 cm and 1000 turns of wire is
A0.86mHB1.06mHC1.26mHD1.46mH
Two wires one of copper and other of iron having same cross-section area and lengths 2 m and 1.5 m respectively are fastened end and stretched by a load 10 N. If copper wire is stretched by 2mm then find the total extension of combined wire, YCu=1×1011N/m2 and YFe=3×1011N/m2.
View SolutionAn electric current of 16 A exists in a metal wire of cross section 10−6m2 and length 1 m. Assuming one free electron per atom. The drift speed of the free electrons in the wire will be (Density of metal = 5×103kg/m3 atomic weight = 60)
View SolutionA light rod of length of length 2m is suspended from a ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross - section 10−3m2 and the other is of brass of cross- section 2×10−3m2.x is the distance from the steel wire end, at which a weight may be hung. Ysteel=2×1011PaandYbrass=1011Pa
Which of the following statement(s) is /are correct ?
View SolutionA light rod of length of length 2m is suspended from a ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross - section 10−3m2 and the other is of brass of cross- section 2×10−3m2.x is the distance from the steel wire end, at which a weight may be hung. Ysteel=2×1011PaandYbrass=1011Pa
Which of the following statement(s) is /are correct ?
View SolutionA block of weight 100 N is suspended by copper and steel wires of same cross sectional area 0.5cm2 and, length √3 m and 1m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are 30∘and60∘, respectively. If elongation in copper wire is (ΔlC) and elongation in steel wire is (Δls), then the ratio ΔlCΔls is -
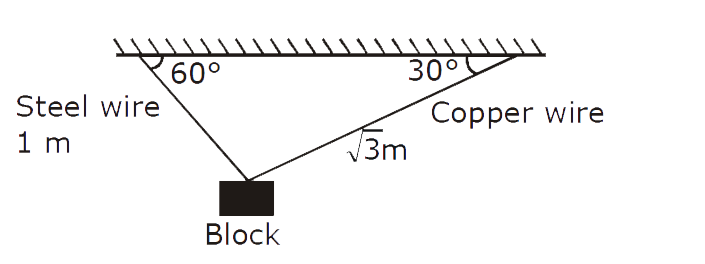
[Young's modulus for copper and steel are 1×1011N/m2and2×1011N/m2, respectively]
View SolutionIf 106 electrons/s are flowing through an area of cross section of 10−4m2 then the current will be:-
View SolutionA steel wire and a copper wire of equal length and equal cross- sectional area are joined end to end and the combination is subjected to a tension. Find the ratio of
copper/steel
(a) the stresses developed . In the two wires,
(b) the strains developed. (Y of steel =2×1011N/m2)
View Solution
