In a midified YDESE, sources S is kept in front of slit S1. Find the phase difference at point O that is equidistant from slits S1 and S2 and point P that is in front of slit S1 in the following situations. ltgt 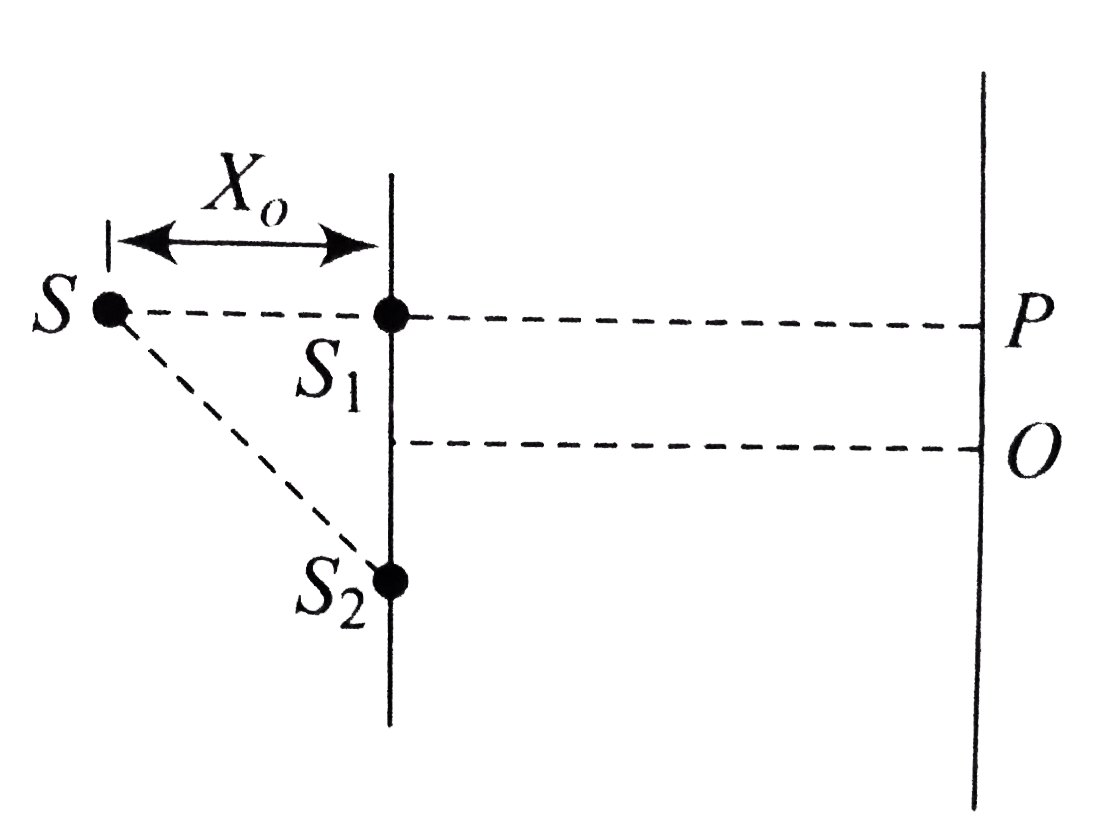
Liquid is filled between the slit and source S.
2πλ=[μ√d2+x20−x0−d22D]
2πλ=[μ√d2+x20−x0+d22D]
2πλ[μ√d2−x20+x0+d22D]
2πλ=[μ√d2+x20+x0+d22D]
The correct Answer is:b
While calculating path difference, it must be remembered that is is equal to difference of optical path lengths from sources S to point on the screen.
∴Δxtotal=[Δx]before slits+[Δx]after slits
=(SS2−SS1)+(S2P−S1P) ltbgt a. When liquid is filled between the slits and screen, then
[S2P]liquid=[μS2P]air
[S1P]liquid=[μS1P]air
At point O: μS2O=μS1O
Noth path difference is introduced after slits. So,
Δxtotal=SS2−SS1=√d2+X20−x0
Thus, phase diffenence,
Δϕ=2πλ(√d2+X20−x0)
At point P: [Delta x]_("before slits") = sqrt(d^(2) + x_(0)^(2)) - x_(0)<br>[Delta x]_("after slits") = mu S_(2) P - mu S_(1) ap = mu (S_(2)P - S_(1)P)<br>= (mu yd)/(D) = (mu d^(2))/(2 D)(asy=d2)
Thus phase difference,
Δϕ=2πλ[(√d2+x20−x0)+μd22D]
b. When liquid is filled between the source and slits:
At point O: (Δx)before slits=(SS2+SS1)liquid
(μSS2+μSS1)air
=μ(√d2+x20−x0)
(Δx)after slits=S2O+S1O=0
(Δx)total=μ(√d2+x20−x0)
Thus, phase differnce at P,
Δϕ=2πλ(μ√d2+x20−x0)
At point P: (Δx)before slits=(SS2+SS1)liquid=(μSS2+μSS1)air
(Δx)after slits=(S2P−S1P)air=ydD=d22D
(Δx)total=[(μ√d2+x20−x0)+d22D]
Thus, phase difference at P,
Δϕ=2πλ[μ√D2+x20−x0+d22D]
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Integer
3 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Archives
4 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
In a modified YDSE, sources S is kept in front of slit S1. Find the phase difference at point O that is equidistant from slits S1 and S2 and point P that is in front of slit S1 in the following situations.
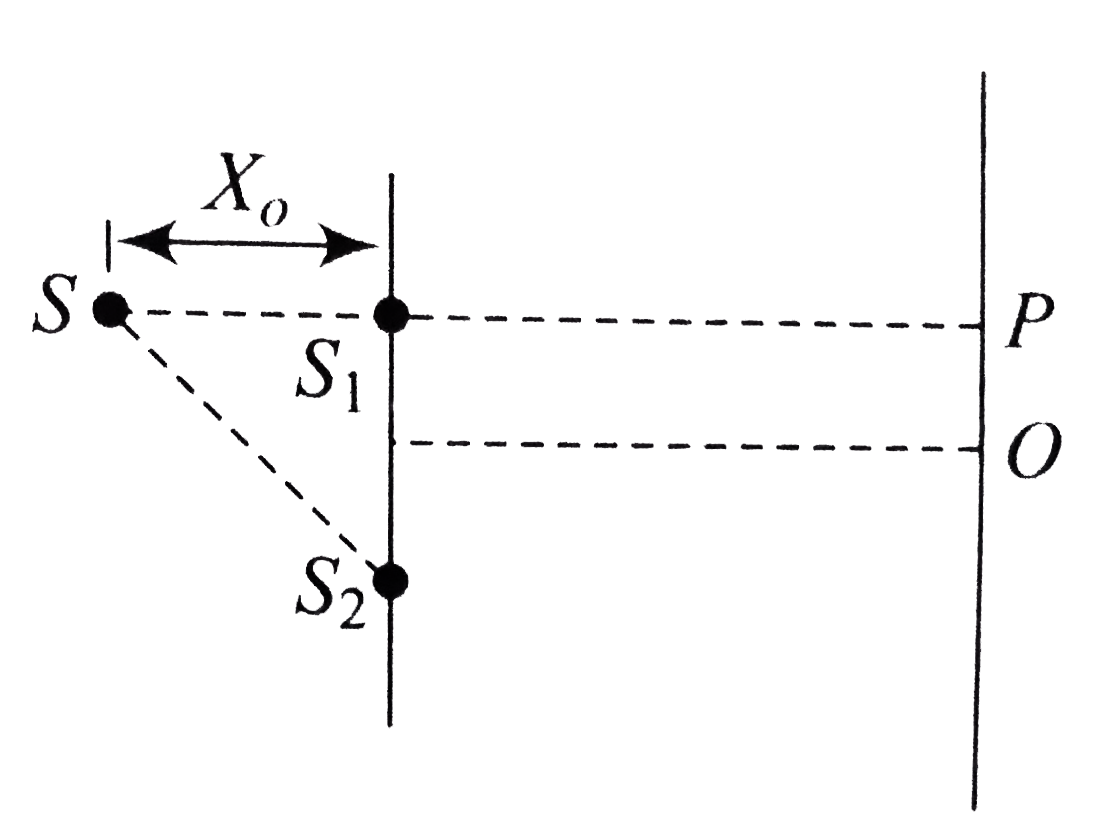
A liquid of refractive index μ is filled between the screen and slits.
View SolutionIn an interference experiment, the two slits S1andS2 are not equidistant from the source S. then the central fringe at 0 will be
View Solution
Knowledge Check
In a modified Young's double-slit experiment, source S is kept in front of slit S1 as shown in the following figure. Find the phase difference at a point that is equidistant from slits S1 and S2 and point P that is in front of slit S1 in the following situations:

If a liquid is filled between the slit and the source S, what is the phase difference?A2πλ[n√d2+x20−x0−d22D]B2πλ[n√d2+x20−x0+d22D]C2πλ[n√d2+x20+x0+d22D]D2πλ[n√d2−x20−x0−d22D]In a modified Young's double-slit experiment, source S is kept in front of slit S1 as shown in the following figure. Find the phase difference at a point that is equidistant from slits S1 and S2 and point P that is in front of slit S1 in the following situations:
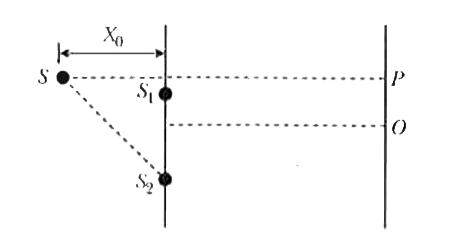
If a liquid of refractive index n is filled between the screen and slits, what is the phase difference?A2πλ[[√d2+x20+x0]+nd22D]B2πλ[[√d2+x20−x0]+nd22D]C2πλ[[√d2−x20+x0]+nd22D]D2πλ[[√d2−x20−x0]+nd22D]A coherent light is incident on two paralle slits S1andS2. At a point P1 the frings will be dark if the phase difference between the rays coming from S1andS2 is
Anπ radiansB(n+0.5)π radiansC(2n+0.5)π radiansD(2n+1)π radians
In the set up shown in figure, the two slits S1 and S2 are not equidistant from the slit S. The central fringe at O is then
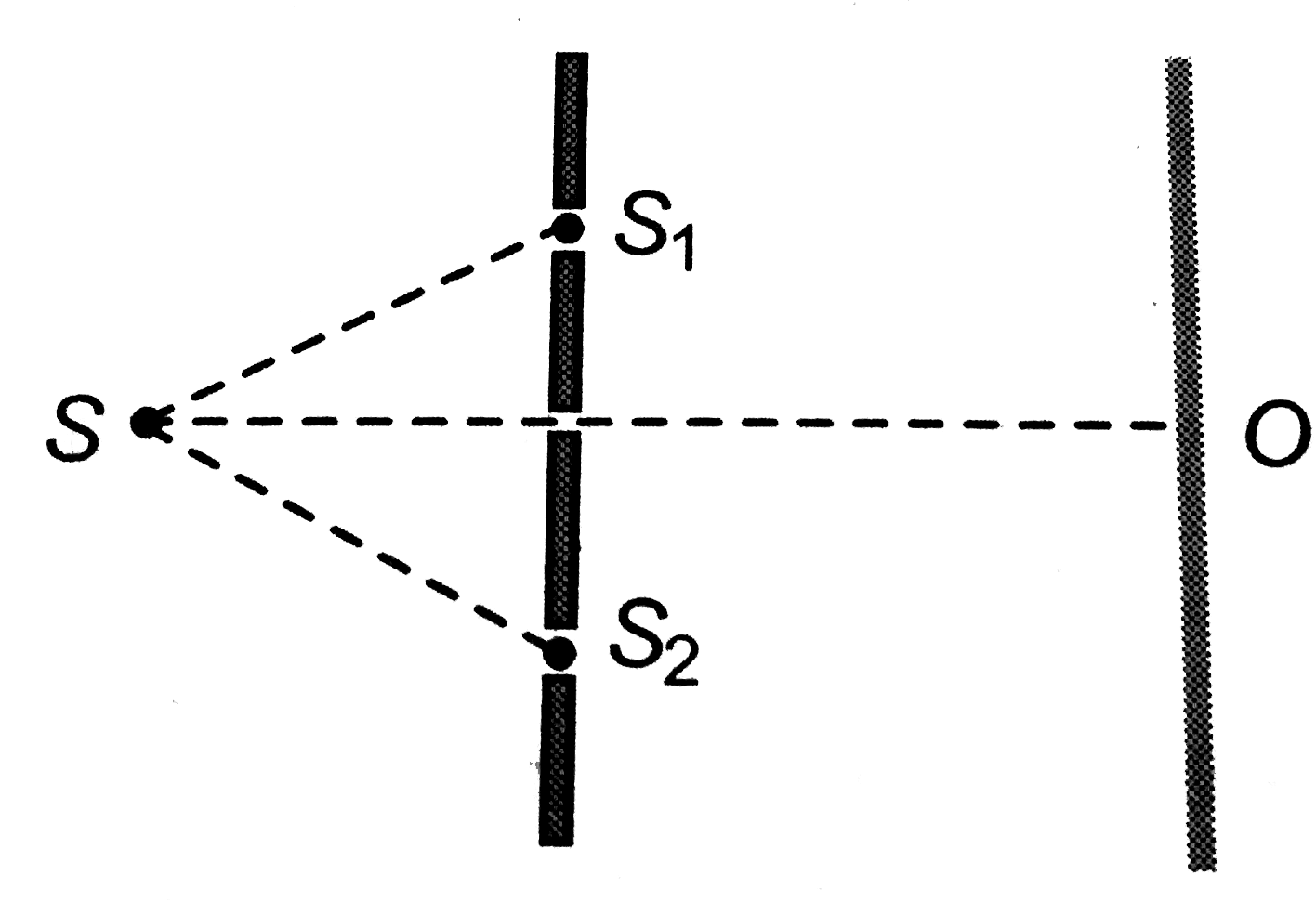
View SolutionMonochromatic light of wavelength λ passes through a very narrow slit S and then strikes a screen placed at a distance D = 1m in which there are two parallel slits S1 and S2 as shown. Slit S1 is directly in line with S while S2 is displaced a distance d to one side. The light is detected at point P on a second screen, equidistant from S1 and S2 When either slit S1 or S2 is open equal light intensities I are measured at point P. When both slits are open, the intensity is three times as large i.e. 3I. If the minimum possible wavelength is Nd2, then find the value of N(d<<D)

View SolutionMonochromatic light of wavelength λ passes through a very narrow slit S and then strikes a screen placed at a distance D = 1m in which there are two parallel slits S1 and S2 as shown. Slit S1 is directly in line with S while S2 is displaced a distance d to one side. The light is detected at point P on a second screen, equidistant from S1 and S2 When either slit S1 or S2 is open equal light intensities I are measured at point P. When both slits are open, the intensity is three times as large i.e. 3I. If the minimum possible wavelength is Nd2, then find the value of N(d<<D)

View SolutionIn a modified set up of Young's double slit experiment, it is given that SS2−SS1=λ4 i.e., the source S is not equidistant from the slits S1andS2.
(a) Obtain the condition for constructive and destructive interference at any point P on the screen in terms of the path difference Δ=S2P−S1P.
(b) Does the observed central bright fringe lie above or below O ? Give reason in support of your answer.
View SolutionIn the set up shown in figure, the two slits S1 and S2 are not equidistant from the slit S. The central fringe at O is then

View Solution
