Consider a collision between two particles one of which is at rest and the other strikes it head on with momentum P1. Calculate the energy of reaction Q in terms of the kinetic energy of the particles before and they collide.
To solve the problem of calculating the energy of reaction Q in terms of the kinetic energy of the particles before they collide, we can follow these steps:
Step 1: Understand the System
We have two particles:
- Particle 1 with mass m1 and initial momentum P1 (moving).
- Particle 2 with mass m2 at rest, so its momentum P2=0.
Step 2: Apply Conservation of Momentum
According to the conservation of momentum, the total momentum before the collision must equal the total momentum after the collision. Thus, we can write:
P1+P2=P′1+P′2
Since P2=0, this simplifies to:
P1=P′1+P′2
Step 3: Express P′2
From the equation above, we can express P′2 as:
P′2=P1−P′1
Step 4: Square the Momentum Terms
To relate momentum to kinetic energy, we square the momentum terms:
P′22=(P1−P′1)2=P21−2P1P′1+P′21
Step 5: Relate Kinetic Energy to Momentum
The kinetic energy K of a particle can be expressed in terms of its momentum P as:
K=P22m
Thus, we can write the kinetic energies before and after the collision:
- Initial kinetic energy of particle 1:
K1=P212m1
- Final kinetic energy of particle 1:
K′1=P′212m′1
- Final kinetic energy of particle 2:
K′2=P′222m′2
Step 6: Write the Energy of Reaction Q
The energy of reaction Q can be defined as the difference in total kinetic energy before and after the collision:
Q=(K1+K2)−(K′1+K′2)
Since particle 2 is initially at rest, its initial kinetic energy K2=0:
Q=K1−(K′1+K′2)
Step 7: Substitute Kinetic Energies
Substituting the expressions for kinetic energy:
Q=P212m1−(P′212m′1+P′222m′2)
Step 8: Substitute P′2
Now substitute P′2 from Step 3 into the equation:
Q=P212m1−(P′212m′1+(P1−P′1)22m′2)
Step 9: Simplify the Expression
This expression can be simplified further to express Q in terms of the kinetic energies of the particles before the collision.
Final Expression for Q
After simplification, we arrive at the final expression for the energy of reaction Q:
Q=P212m1−(P′212m′1+(P1−P′1)22m′2)
We have two particles:
- Particle 1 with mass m1 and initial momentum P1 (moving).
- Particle 2 with mass m2 at rest, so its momentum P2=0.
According to the conservation of momentum, the total momentum before the collision must equal the total momentum after the collision. Thus, we can write:
P1+P2=P′1+P′2
Since P2=0, this simplifies to:
P1=P′1+P′2
From the equation above, we can express P′2 as:
P′2=P1−P′1
To relate momentum to kinetic energy, we square the momentum terms:
P′22=(P1−P′1)2=P21−2P1P′1+P′21
The kinetic energy K of a particle can be expressed in terms of its momentum P as:
K=P22m
Thus, we can write the kinetic energies before and after the collision:
- Initial kinetic energy of particle 1:
K1=P212m1
- Final kinetic energy of particle 1:
K′1=P′212m′1
- Final kinetic energy of particle 2:
K′2=P′222m′2
The energy of reaction Q can be defined as the difference in total kinetic energy before and after the collision:
Q=(K1+K2)−(K′1+K′2)
Since particle 2 is initially at rest, its initial kinetic energy K2=0:
Q=K1−(K′1+K′2)
Substituting the expressions for kinetic energy:
Q=P212m1−(P′212m′1+P′222m′2)
Now substitute P′2 from Step 3 into the equation:
Q=P212m1−(P′212m′1+(P1−P′1)22m′2)
This expression can be simplified further to express Q in terms of the kinetic energies of the particles before the collision.
After simplification, we arrive at the final expression for the energy of reaction Q:
Q=P212m1−(P′212m′1+(P1−P′1)22m′2)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Solved Examples17videos
NUCLEAR PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Exercise 5.110videos
NUCLEAR PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Integer Type4videos
PHOTOELECTRIC EFFECT
Similar Questions
Knowledge Check
- Question 1 - Select One
For a moving particle (mass m, velocity v) having a momentum p, which one of the following correctly describes the kinetic energy of the particle?
Ap22mBp2mCv22mDv2m
Consider a system of two identical particles. One of the particles is at rest and the other has an acceleration. The centre of mass has an acceleration.
View Solutionconsider a head on collision between two particles of masses m1andm2. The initial speeds of the particles are u1andu2 in the same direction. The collision starts at t=0 and the particles interact for a time interval △t. during the collision the speed of the first particle varies as
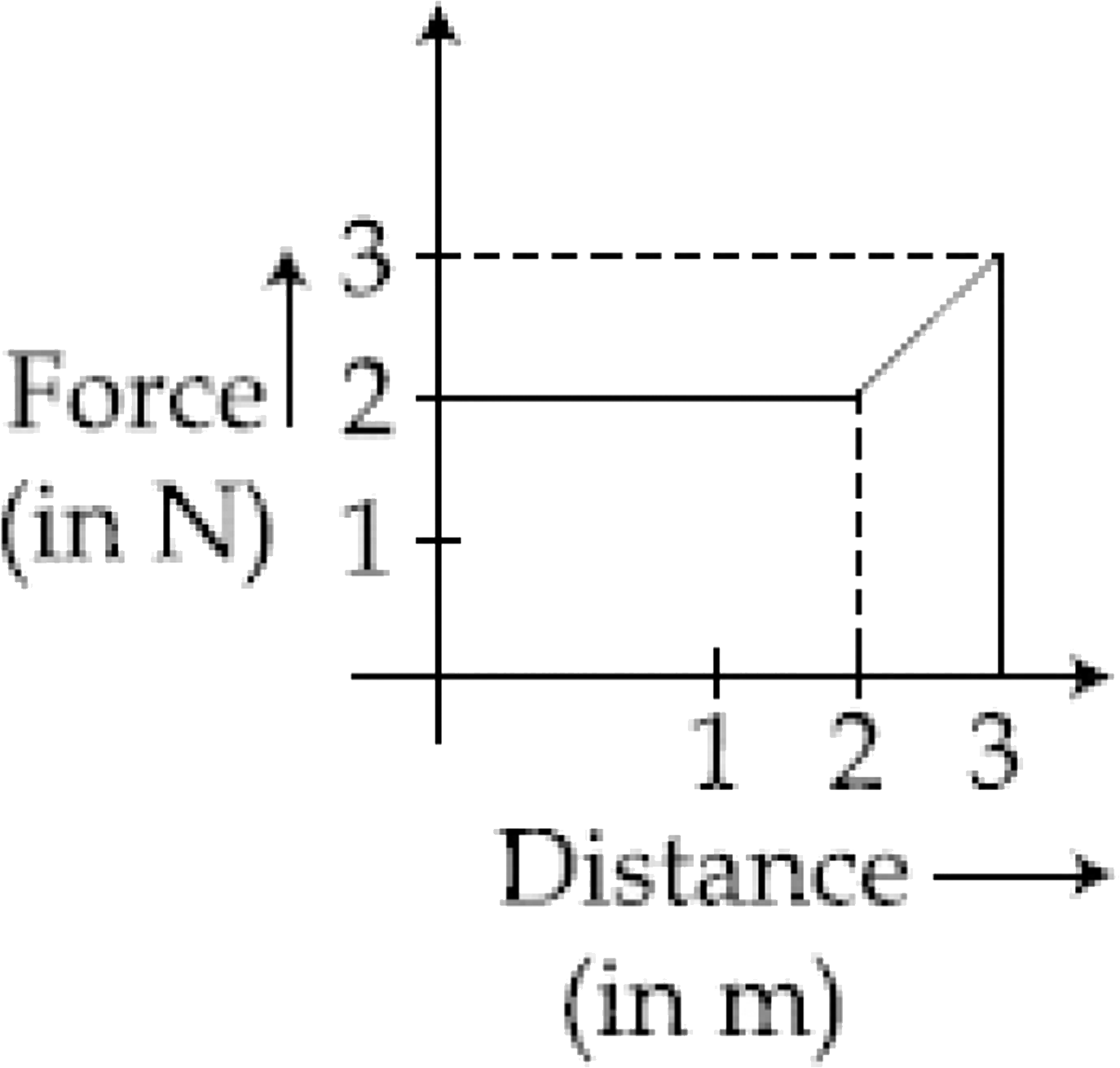
v(t)=u1+t/ t(v1−u1) Find the speed of the second particle as as function of time during the collision.View SolutionA particle moves in one dimension from rest under the influence of a force that varies with the distance travelled by the particle as shown in the figure. The kinetic energy of the particle after it has travelled 3m is:
 View Solution
View SolutionConsider the following two statements:
A. Linear momentum of a system of particles is zero.
B. Kinetic energy of a system of particles is zero.View SolutionA particle of mass m and charge q is released from rest in uniform electric field of intensity E. Calculate the kinetic energy it attains after moving a distance y between the plates.
View SolutionA moving body of mass m makes a head on elastic collision with another body of mass 2m which is initially at rest. Find the fraction of kinetic energy lost by the colliding particles after collision.
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View Solution


