For a series RLC circuit R=XL=2XC. The impedence of the current and phase different (between) V and i will be
√5R2,tan−1(2)
√5R2,tan−1(12)
√5XC,tan−1(12)
√5R,tan−1(12)
The correct Answer is:B
To solve the problem step by step, we will analyze the given conditions and apply the relevant formulas for impedance and phase difference in a series RLC circuit.
Step 1: Understand the given conditions
We are given that:
- R=XL=2XC
Step 2: Express XL and XC in terms of R
From the given condition, we can express:
- XL=R
- XC=R2
Step 3: Write the formula for impedance Z
The impedance Z in a series RLC circuit is given by:
Z=√R2+(XL−XC)2
Step 4: Substitute the values of R, XL, and XC
Substituting XL=R and XC=R2 into the impedance formula:
Z=√R2+(R−R2)2
This simplifies to:
Z=√R2+(R2)2
Step 5: Simplify the expression for Z
Calculating (R2)2:
(R2)2=R24
Now substituting this back into the impedance formula:
Z=√R2+R24=√4R24+R24=√5R24=R2√5
Step 6: Calculate the phase difference ϕ
The phase difference ϕ is given by:
tanϕ=XL−XCR
Substituting the values:
tanϕ=R−R2R=R2R=12
Step 7: Find ϕ
To find ϕ, we take the arctangent:
ϕ=tan−1(12)
Conclusion
The impedance of the circuit is R2√5 and the phase difference ϕ is tan−1(12).
We are given that:
- R=XL=2XC
From the given condition, we can express:
- XL=R
- XC=R2
The impedance Z in a series RLC circuit is given by:
Z=√R2+(XL−XC)2
Substituting XL=R and XC=R2 into the impedance formula:
Z=√R2+(R−R2)2
This simplifies to:
Z=√R2+(R2)2
Calculating (R2)2:
(R2)2=R24
Now substituting this back into the impedance formula:
Z=√R2+R24=√4R24+R24=√5R24=R2√5
The phase difference ϕ is given by:
tanϕ=XL−XCR
Substituting the values:
tanϕ=R−R2R=R2R=12
To find ϕ, we take the arctangent:
ϕ=tan−1(12)
The impedance of the circuit is R2√5 and the phase difference ϕ is tan−1(12).
Topper's Solved these Questions
- ALTERNATING CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:ALTERNATING CURRENTExercise:Comphension Based
Explore 8 Videos
- ALTERNATING CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:ALTERNATING CURRENTExercise:Single Correct
Explore 10 Videos
- ALTERNATING CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:ALTERNATING CURRENTExercise:Archives Integer
Explore 1 Video
- ATOMIC PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:ATOMIC PHYSICSExercise:ddp.4.3
Explore 15 Videos
Similar Questions
Knowledge Check
In a series LCR circuit, the phase difference between the voltage and the current is 45∘. Then the power factor will be
A0.607B0.707C0.808D1
In a series LCR circuit resistance R=10Ω and the impedance Z=10Ω The phase difference between the current and the voltage is
View SolutionFind the phase difference between voltage and current in L-C circuit.
View SolutionIn the shown AC circuit phase different between current I1 and I2 is
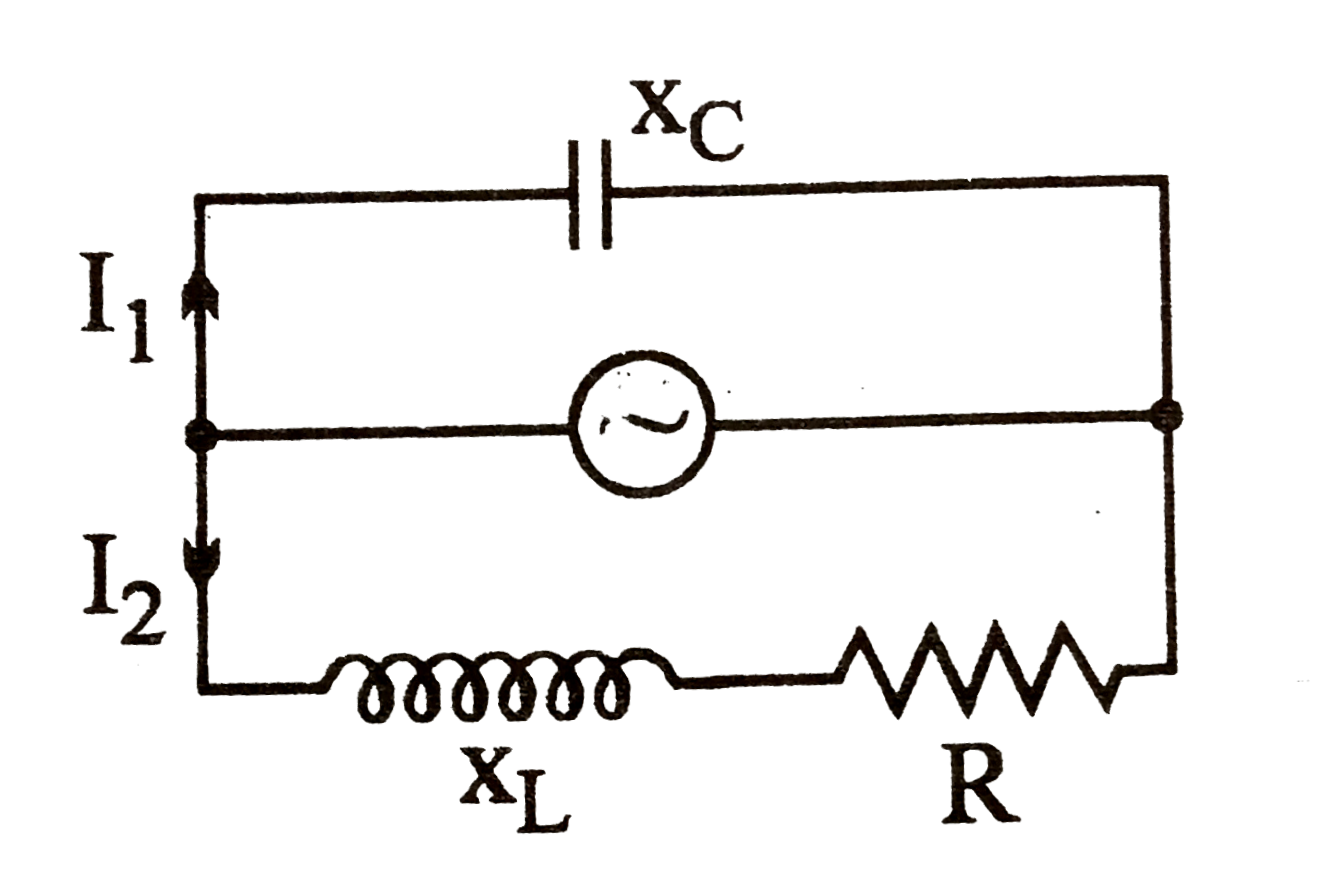
View SolutionIn the circuit shown in figure :
R=10Ω,L=√310H,R2=20Ω and C=√32mF. Current in L−R1 circuit is I1 in C−R1 circuit is I2 and the main current is I

Phase difference between I1 and I2 is
View SolutionIn the circuit shown in figure :
R=10Ω,L=√310H,R2=20Ω and C=√32mF. Current in L−R1 circuit is I1 in C−R1 circuit is I2 and the main current is I

Phase difference between I1 and I2 is
View Solution200V A.C. is applied at the ends of an LCR circuit. The circuit consists of an inductive reactance XL=50Ω capacitive reactance Xc=50Ω and ohmic resistance R = 10 Ω . Calculate the impedance of the circuit and also potential differences across L and R What will be the potential difference across L-C
View Solutionin a series LCR circuit, what is the phase difference between VLandVC where VL is the potential difference across the inductor and VC is the potential difference across the capacitor?
View Solution