He,N2, and O3 are expanded adiabatically and their expansion curves between P and V are plotted under silimar conditions. About the ratio of the slope, which one is not correct?
The ratio of slopes of P−V curves for He and O3is1.25.
The ratio of slopes of P−V curves for He and N2is1.20.
The ratio of slopes of P−V curves for N2 and O3is1.05.
The slope of He is least steeper and for O3 is most steeper.
To solve the problem regarding the adiabatic expansion of helium (He), nitrogen (N₂), and ozone (O₃), we need to analyze the slopes of their respective P-V curves based on the adiabatic process. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Adiabatic Process
The adiabatic process for an ideal gas is described by the equation:
PVγ=constant
where γ (gamma) is the adiabatic index, defined as:
γ=CpCv
where Cp is the heat capacity at constant pressure and Cv is the heat capacity at constant volume.
Step 2: Differentiate the Adiabatic Equation
To find the slope of the P-V curve, we differentiate the equation PVγ=constant with respect to V:
ddV(PVγ)=0
Using the product rule, we have:
P⋅ddV(Vγ)+Vγ⋅dPdV=0
Step 3: Solve for the Slope dPdV
Differentiating Vγ:
ddV(Vγ)=γVγ−1
Substituting back, we get:
P⋅γVγ−1+Vγ⋅dPdV=0
Rearranging gives:
dPdV=−γPV
Step 4: Calculate γ for Each Gas
- For Helium (He, monoatomic):
- Degrees of freedom F=3
- γ=1+2F=1+23=53
- For Nitrogen (N₂, diatomic):
- Degrees of freedom F=5
- γ=1+25=75
- For Ozone (O₃, triatomic):
- Degrees of freedom F=6
- γ=1+26=43
Step 5: Analyze the Slopes
The slope of the P-V curve is proportional to −γ. Thus, we can compare the slopes:
- Slope for He: −53
- Slope for N₂: −75
- Slope for O₃: −43
Step 6: Calculate Ratios of Slopes
1. He to O₃:
Ratio=−53−43=54=1.25
2. He to N₂:
Ratio=−53−75=2521≈1.19
3. N₂ to O₃:
Ratio=−75−43=2120=1.05
Step 7: Conclusion
From the calculations, we can conclude that the slopes of the P-V curves for these gases are related to their respective γ values. The incorrect statement regarding the ratios of slopes can be identified based on the calculated values.
The adiabatic process for an ideal gas is described by the equation:
PVγ=constant
where γ (gamma) is the adiabatic index, defined as:
γ=CpCv
where Cp is the heat capacity at constant pressure and Cv is the heat capacity at constant volume.
To find the slope of the P-V curve, we differentiate the equation PVγ=constant with respect to V:
ddV(PVγ)=0
Using the product rule, we have:
P⋅ddV(Vγ)+Vγ⋅dPdV=0
Differentiating Vγ:
ddV(Vγ)=γVγ−1
Substituting back, we get:
P⋅γVγ−1+Vγ⋅dPdV=0
Rearranging gives:
dPdV=−γPV
- For Helium (He, monoatomic):
- Degrees of freedom F=3
- γ=1+2F=1+23=53
- Degrees of freedom F=5
- γ=1+25=75
- Degrees of freedom F=6
- γ=1+26=43
The slope of the P-V curve is proportional to −γ. Thus, we can compare the slopes:
- Slope for He: −53
- Slope for N₂: −75
- Slope for O₃: −43
1. He to O₃:
Ratio=−53−43=54=1.25
Ratio=−53−75=2521≈1.19
Ratio=−75−43=2120=1.05
From the calculations, we can conclude that the slopes of the P-V curves for these gases are related to their respective γ values. The incorrect statement regarding the ratios of slopes can be identified based on the calculated values.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise
1 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Ex 6.1
26 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
V vs T curves at constant pressure P1 and P2 for an ideal gas are shown in the figure. Which of the following is correct?

View SolutionThe reversible expansion of an ideal gas under adiabatic and isothermal conditions is shown in the figure. Which of the following statement(s) is (are) correct?
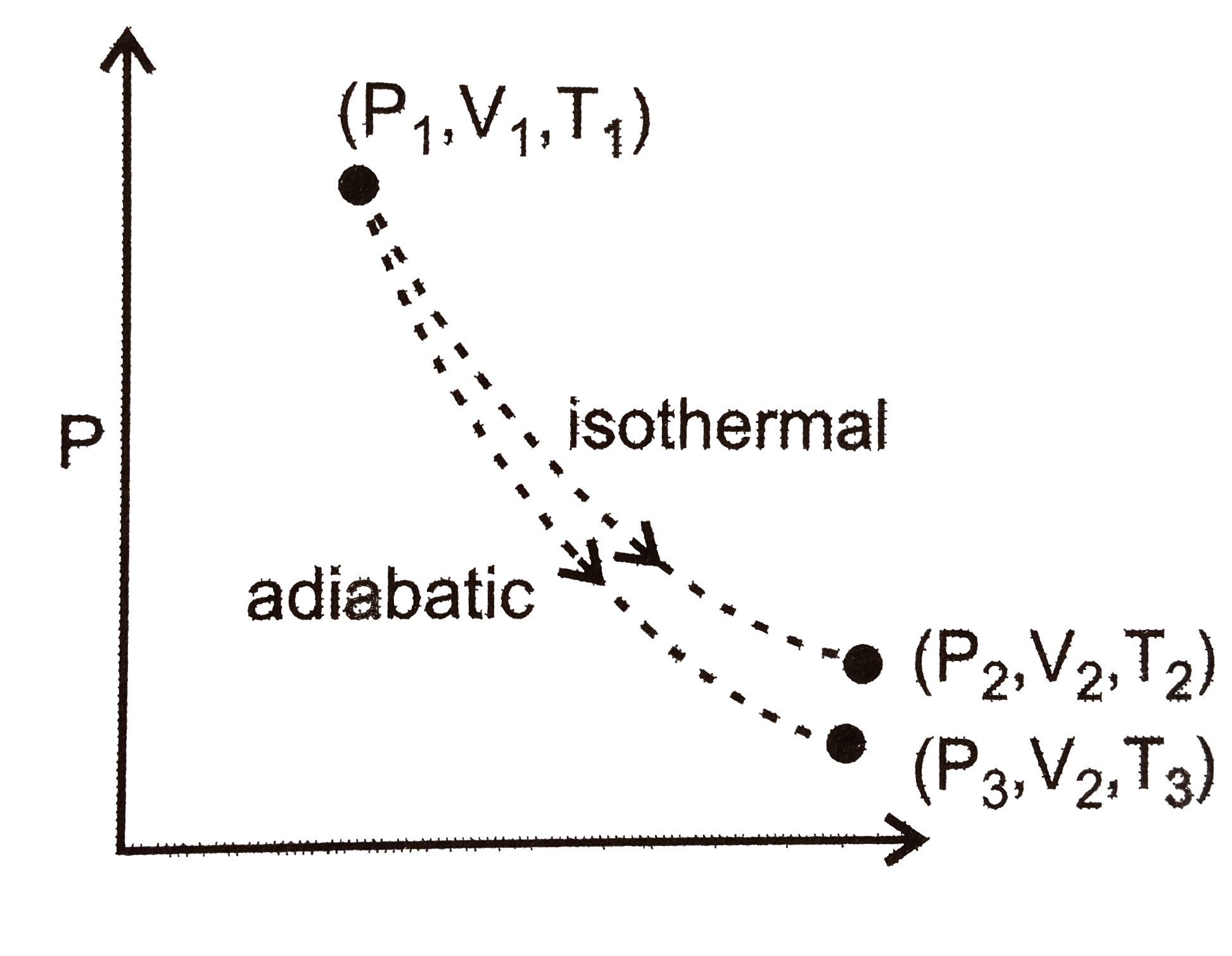
View SolutionV vs T curves at different pressures P1 and P2 for an ideal gas are shown below:
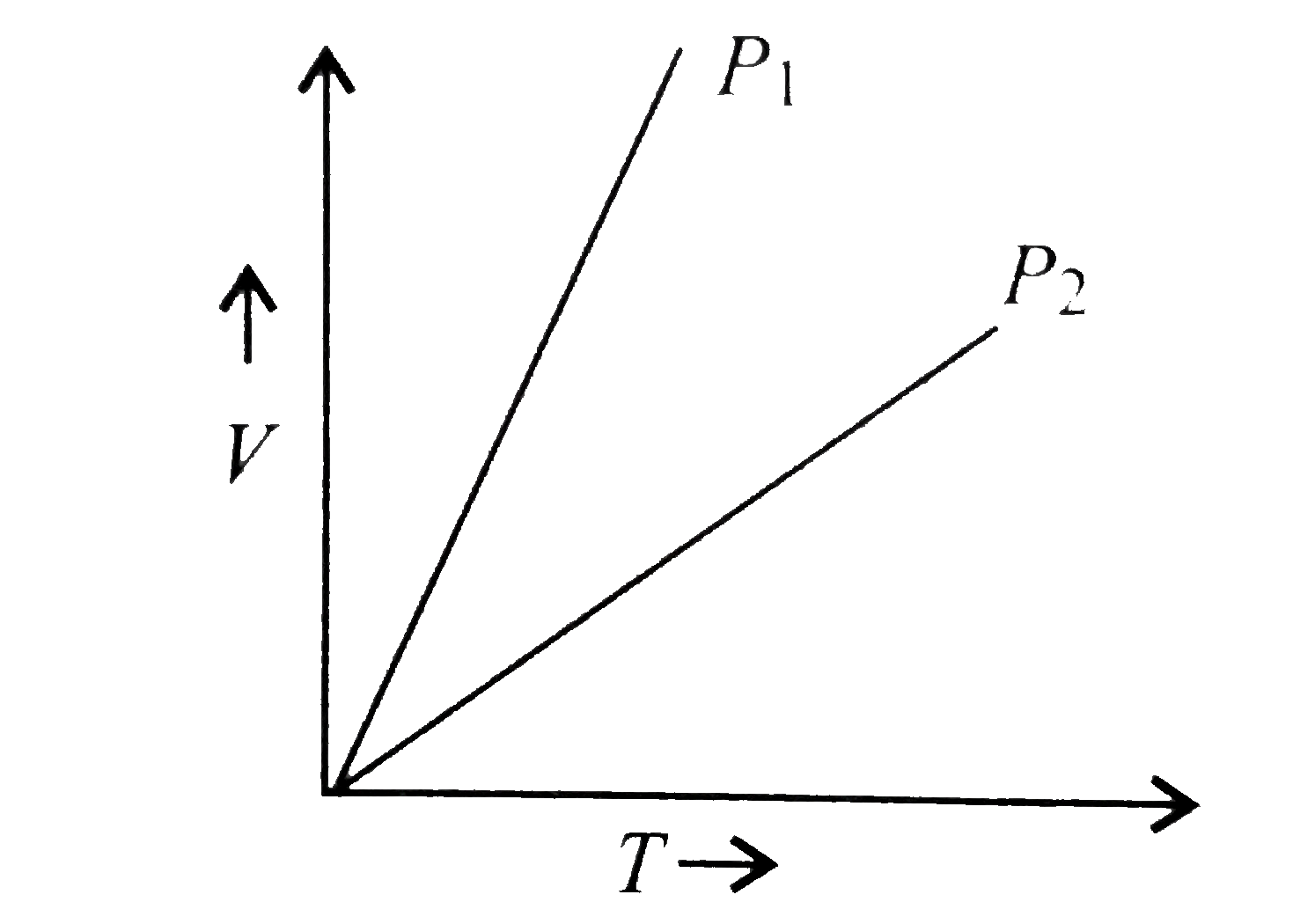
Which one of the following is correct?
View SolutionIf a graph is plotted between 1/v and 1/u , which one of the graph shown in figure is approximately correct ?
View SolutionStatement-1: Temperature of a system can be increased without supplying heat.
Statement-2: If the initial volume of system is equal to final volume in a process then work done is necessarily zero.
Statement-3: If an adiabatic curve for a gas intersect with an isothermal curve for the same gas then at the point of intersection, the ratio of slope of the adiabatic and the isothermal curve is γ.
View SolutionIf helium and oxygen gas are allowed to escape out of a container containing equal amount of He and O2 under slmllar conditions of temperature and pressure the ratio of rate of diffusion of O2 to that of He is
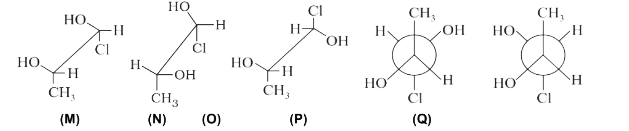
View SolutionWhich of the given statements about N,O,P and d Q with respect to M is correct ?
View SolutionAn ideal gas is initially at P1,V1 is expands to P2,V2 isothermally and then compressed adiabatically to the same volume V1 and pressure P3. If W is the net work done by the gas in complete process which of the following is true.
View SolutionAn ideal gas is initially at P1,V1 is expands isothermally to P2,V2 and then compressed adiabatically to the same volume V1 and pressure P3. If W is the net work done by the gas in complete process which of the following is true.
View SolutionAn ideal gas expands from V to 2V in 4 separate processes. Where process 1 is isothermal process 2 is adiabatic, process 3 is free expansion and process 4 is isobaric. If E1,E2,E3 and E4 are the changes in average kinetic energy of the molecules in the isothermal, adiabatic free expansion and isobaric process respectively then choose the correct options.
View Solution
