The coordinates of a triangle ABC are A(1,2), B(4,6) and C(−3,−2). Three particles of masses 1kg, 2kg and mkg are placed the vertices of the triangle. If the coordinate of the centre of mass are (35,2), calculate the mass m.
To solve the problem, we need to find the mass m of the third particle placed at vertex C of triangle ABC given the coordinates of the vertices and the center of mass.
1. Identify the Given Data:
- Coordinates of points:
- A(1,2)
- B(4,6)
- C(−3,−2)
- Masses:
- m1=1kg (at point A)
- m2=2kg (at point B)
- m3=mkg (at point C)
- Center of mass coordinates: (35,2)
2. Use the Formula for Center of Mass:
The coordinates of the center of mass (CM) for a system of particles is given by:
xcm=m1x1+m2x2+m3x3m1+m2+m3
ycm=m1y1+m2y2+m3y3m1+m2+m3
3. Set Up the Equation for the x-coordinate:
Substitute the known values into the x-coordinate formula:
35=1⋅1+2⋅4+m⋅(−3)1+2+m
Simplifying the numerator:
35=1+8−3m3+m
35=9−3m3+m
4. Cross-Multiply to Eliminate the Fraction:
3(3+m)=5(9−3m)
Expanding both sides:
9+3m=45−15m
5. Combine Like Terms:
Move all terms involving m to one side:
3m+15m=45−9
18m=36
6. Solve for m:
m=3618=2kg
7. Verify with the y-coordinate:
To ensure correctness, we can also check using the y-coordinate:
2=1⋅2+2⋅6+m⋅(−2)1+2+m
Simplifying:
2=2+12−2m3+m
Cross-multiplying:
2(3+m)=14−2m
Expanding:
6+2m=14−2m
Combining like terms:
4m=8⟹m=2kg
Final Answer:
The mass m is 2kg.
- Coordinates of points:
- A(1,2)
- B(4,6)
- C(−3,−2)
- Masses:
- m1=1kg (at point A)
- m2=2kg (at point B)
- m3=mkg (at point C)
- Center of mass coordinates: (35,2)
The coordinates of the center of mass (CM) for a system of particles is given by:
xcm=m1x1+m2x2+m3x3m1+m2+m3
ycm=m1y1+m2y2+m3y3m1+m2+m3
Substitute the known values into the x-coordinate formula:
35=1⋅1+2⋅4+m⋅(−3)1+2+m
Simplifying the numerator:
35=1+8−3m3+m
35=9−3m3+m
3(3+m)=5(9−3m)
Expanding both sides:
9+3m=45−15m
Move all terms involving m to one side:
3m+15m=45−9
18m=36
m=3618=2kg
To ensure correctness, we can also check using the y-coordinate:
2=1⋅2+2⋅6+m⋅(−2)1+2+m
Simplifying:
2=2+12−2m3+m
Cross-multiplying:
2(3+m)=14−2m
Expanding:
6+2m=14−2m
Combining like terms:
4m=8⟹m=2kg
The mass m is 2kg.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration4videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)62videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))5videos
SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE21videos
TEST 1
Similar Questions
Knowledge Check
- Question 1 - Select One
Three particles of masses 1kg,32kg,and2kg are located the vertices of an equilateral triangle of side a. The x,y coordinates of the centre of mass are.
Aa. 5a9,2a3√3Bb. 2a3√3,5a9Cc. 5a9,2a√3Dd. 2a√3,5a9
Three particles of masses 0.50 kg, 1.0 kg and are placed at the corners of a right angle triangle, as shown in fig. Locate the centre of mass of the system.
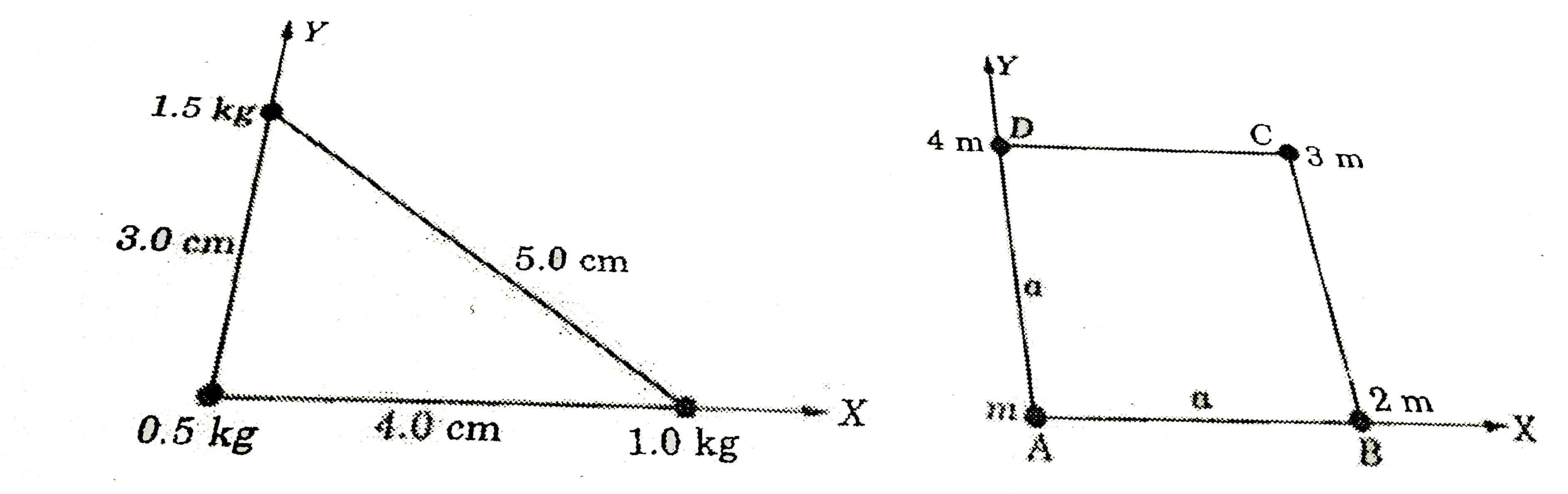 View Solution
View SolutionA(-1, 3), B(4, 2) and C(3, -2) are the vertices of a triangle.
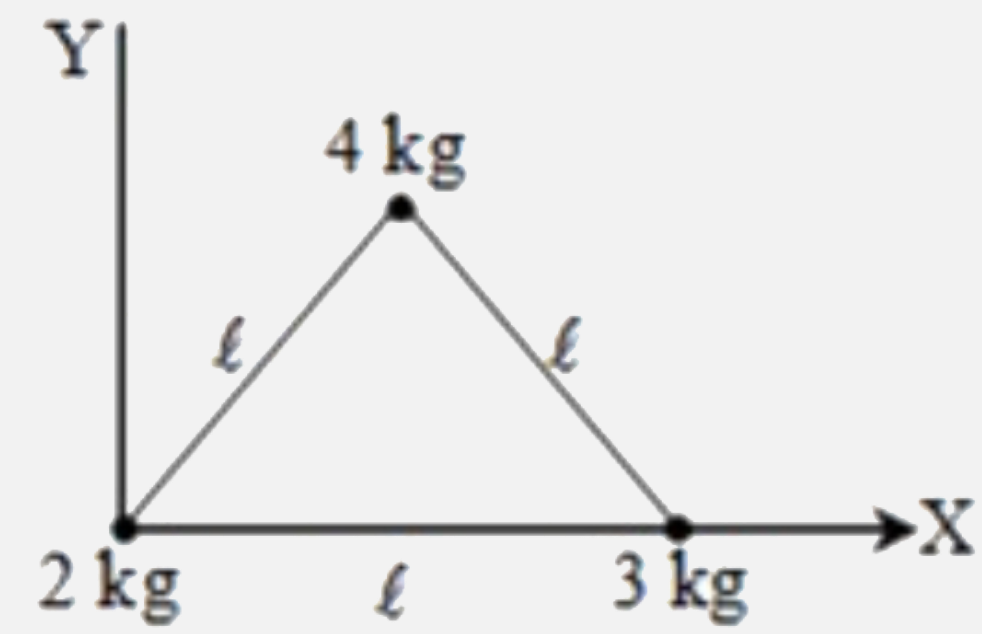
Find the coordinates of the centroid G of the triangle.View SolutionThree particles of masses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre of mass of the system.
View SolutionTwo bodies of masses 1 kg and 2 kg are located at (1,2) and (-1,3), respectively. Calculate the coordinates of center of mass.
View SolutionThree particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
View SolutionThree point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle as shown in figure. The centre of mass of the system is at a point :
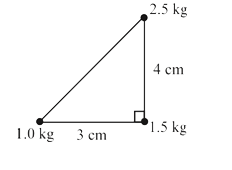 View Solution
View Solution