A unifrom rod of mass m and length L is kept on a horizontal table with L4 length on the table. The end B is tied to a string as shown in the figure. The string attached to the end B is cut and the rod starts rotating about point C. Find the normal reaction from the table on the earth as soon as the string is cut.

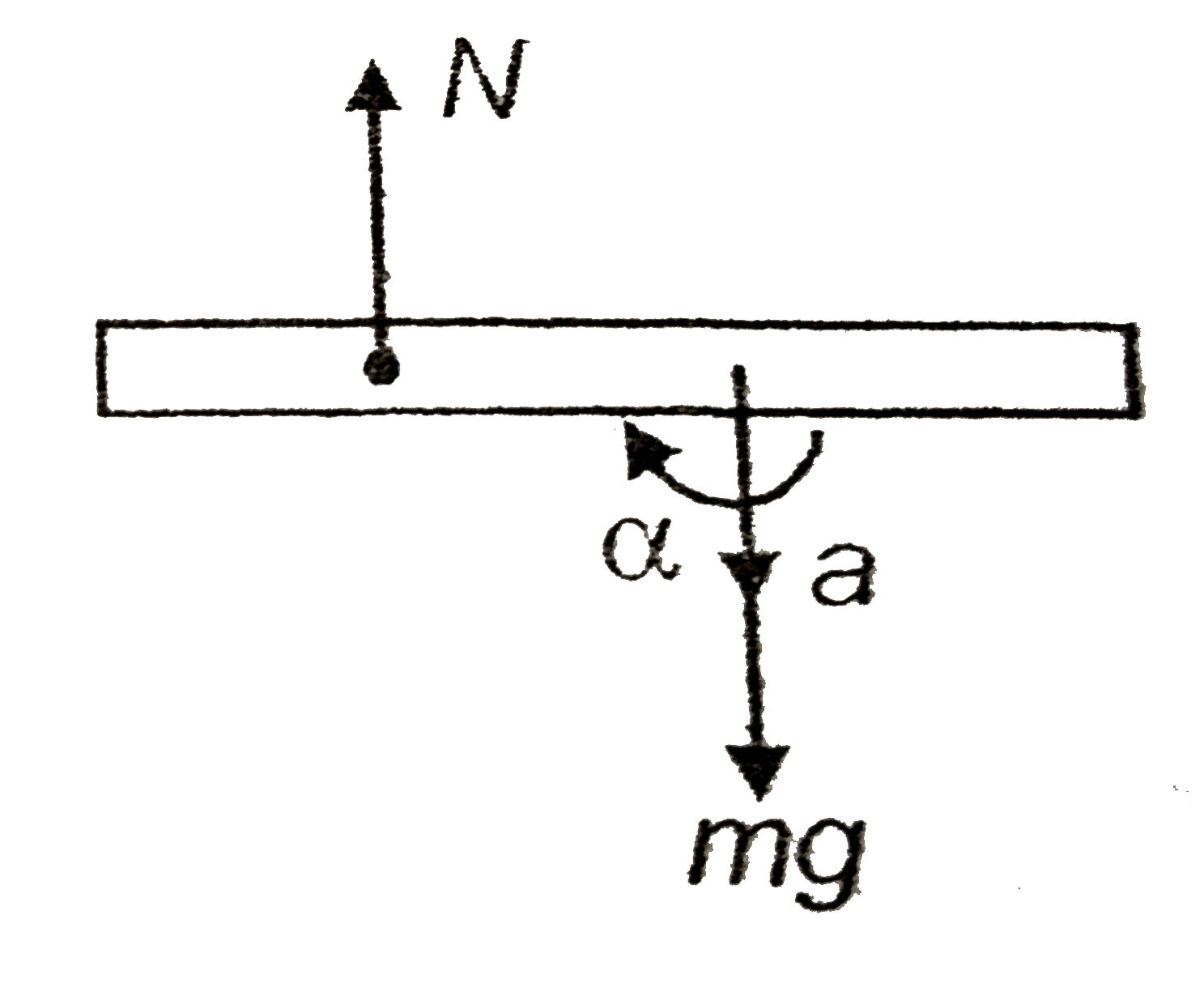
The free body diagram of the rod is as shown in figure.
Here the normal force will shift to the point C and we are assuming that the rod is rotating about C with angular acceleration α. Since C is a stationary point, applying Newton's second law in rotation from about C.
or ∑τ=lα
or mg.L4={mL212+m(L4)2}⋅α
or mg.L4=7mL248⋅α
α=12g7L
⇒aCM=α.r=12g7L×L4=3g7
Applying Newton's Second Law in translational form,
∑F=maCM⇒mg−N=3mg7
⇒N=4mg7

Alternate Method :
You can solve this questions by applying Newton's Second Law in rotational torm about CM of rod.
ΣτCM=lCM.α
⇒N.L4=mL212.α⇒N=mLα3 ...(i)
Sigma F = ma_(CM)<br>rArr mg - N = ma...(2)<br>Sincep∮Cis∈contactwiththetab≤,soitsae≤rationwillbezer⊙<br>a-(alpha L)/(4) = 0 rArr a = (alpha L)/(4)...(3)<br>Solv∈gabovethreeequations,we≥t<br>N = (4mg)/(7)<br>Note:Thevalueofalphaaboutcentreofmassofrodalpha = (12g)/(7L) is same as that about point C.

Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
A uniform rod of mass m and length L is kept on a horizontal table with L4 length on the table as shown in figure. As the string attached to the end B is cut, the angular acceleration of the rod about point C will be
_PHY_E05_242_Q01.png)
View SolutionA horizontal rod of mass M and length L is tied to two verticle string symmetrically as shown in the figure. One of the strings at end Q is cut at t=0 and the rod starts rotating about the other and P then

View SolutionA rod of mass m and length l is lying on a horizontal table. Work done in making it stand on one end will be
View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in the figure. When string is cut, the initial angular accleration of the rod is.

View SolutionA uniform thin rod has mass m and length l. One end of the rod lies over rough horizontal surface and the other end is connected to a light vertical string as shown in the figure. When string is cut, there is no slipping between rod and surface.Calculate the friction force (in N) on the rod immediately after the string is cut .(Given mg=16√3N)

View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:


View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the intial angular acceleration of the rod is

View SolutionA uniform rod of mass m length l is attached to smooth hinge at end A and to a string at end B as shown in figure. It is at rest. The angular acceleration of the rod just after the string is cut is :

View SolutionA uniform rod of mass m and length l is suspended by means of two light inextensible strings as shown in figure. Tension in one string immediately after the other string is cut is

View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:

View Solution
