A sphere of radius R is placed near a long straight wire that carries a steady current l. The magnetic field generated by the current is B. The total magnetic flux passing through the sphere is
Zero
Need more information
The correct Answer is:C
To solve the problem of finding the total magnetic flux passing through a sphere placed near a long straight wire carrying a steady current, we can follow these steps:
1. Understand the Setup: We have a long straight wire carrying a current I and a sphere of radius R placed near this wire. The magnetic field B generated by the current in the wire will affect the sphere.
2. Magnetic Field Due to the Wire: The magnetic field B at a distance D from a long straight wire carrying current I is given by the formula:
B=μ0I2πD
where μ0 is the permeability of free space.
3. Magnetic Flux Definition: The magnetic flux Φ through a surface is defined as:
Φ=∫B⋅dS
where dS is an infinitesimal area element of the surface through which the magnetic field lines pass.
4. Applying Gauss's Law for Magnetism: According to Gauss's law for magnetism, the net magnetic flux through any closed surface is zero. This is because magnetic field lines are continuous loops; they do not begin or end at any point (there are no magnetic monopoles). Thus, the number of magnetic field lines entering a closed surface equals the number of lines leaving it.
5. Conclusion: Since the sphere is a closed surface, the total magnetic flux Φ through the sphere is:
Φ=0
Final Answer:
The total magnetic flux passing through the sphere is Φ=0.
---
B=μ0I2πD
where μ0 is the permeability of free space.
Φ=∫B⋅dS
where dS is an infinitesimal area element of the surface through which the magnetic field lines pass.
Φ=0
The total magnetic flux passing through the sphere is Φ=0.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Assignment (SECTION - B)
Explore 22 Videos
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Assignment (SECTION - C)
Explore 10 Videos
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Try Yourself
Explore 42 Videos
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTE ENGLISHChapter:ELECTRIC CHARGES AND FIELDS Exercise:comprehension
Explore 3 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:ASSIGNMENT SECTION - D Assertion-Reason Type Questions
Explore 25 Videos
Similar Questions
AB and CD are long straight conductor, distance d apart, carrying a current l. The magnetic field at the midpoint of BC is

View SolutionA circular loop of radius r carries a current i. where should a long , straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
View SolutionA long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionA circular loop of radius r carries a current i. How should a long, straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the center becomes zero?
View SolutionA long straight wire of radius a carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetis field at (a)/(2)and(2a) is
View SolutionA long current carrying wire is bent as shown. The magnetic field induction at O is

View SolutionA square loop is placed near a long straight current carrying wire as shown. Match the following table.
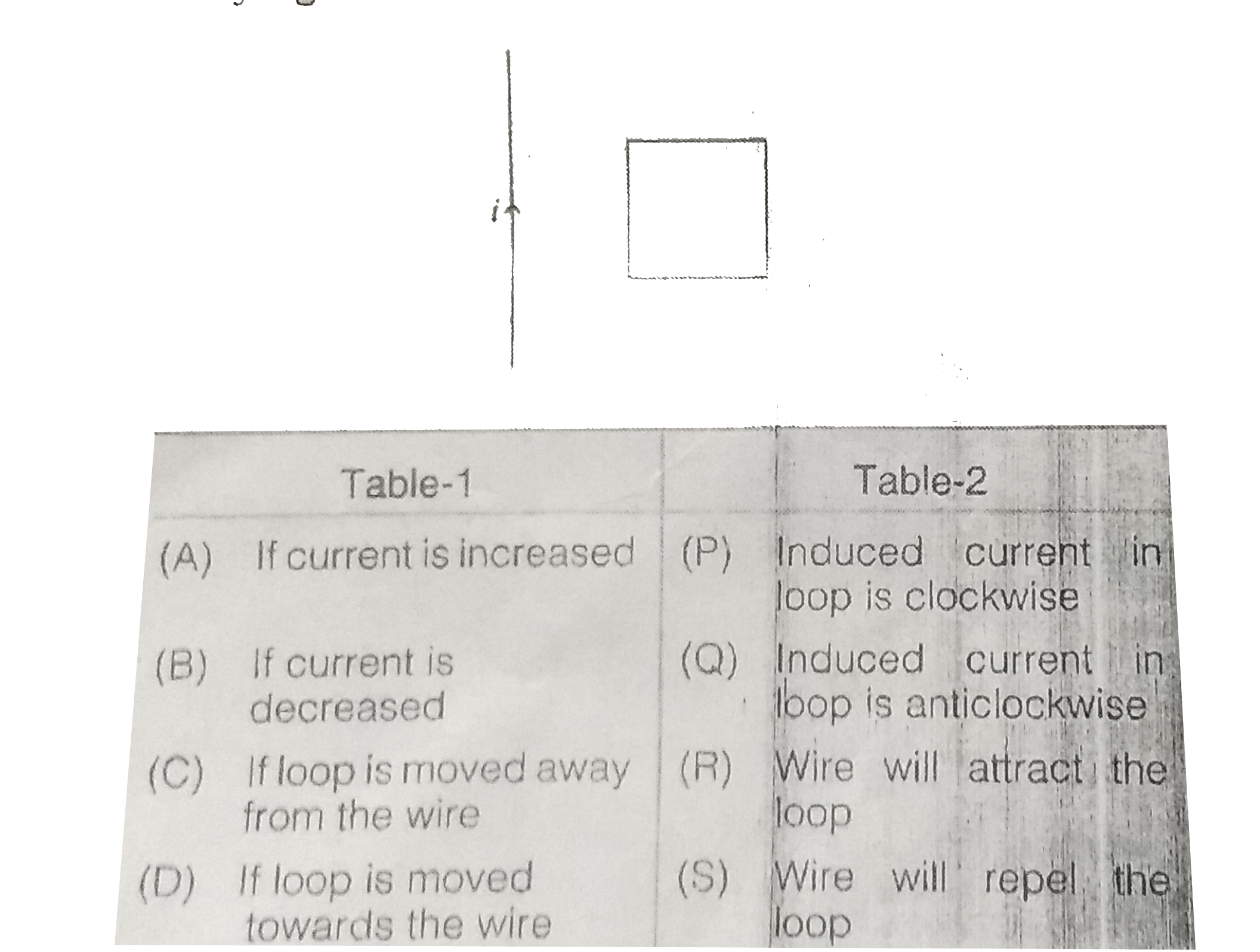
View SolutionA current of 2 amp. flows in a long, straight wire of radius 2mm. The intensity of magnetic field on the axis of the wire is
View SolutionA rectangular loop carrying a current i2 situated near a long straight wire carrying a steady current i1. The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
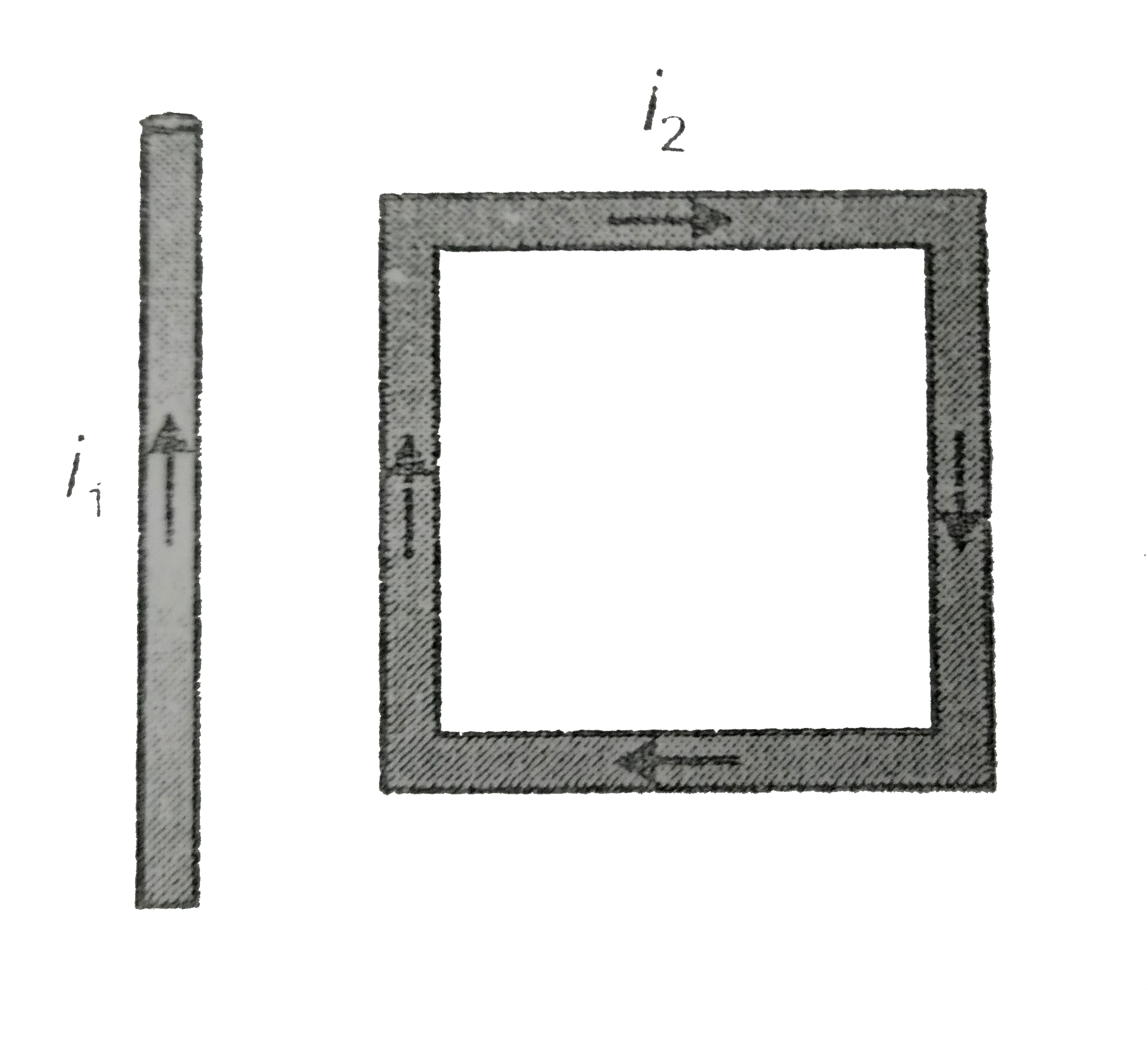
View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View Solution
