A rectangular loop of wire is placed perpendicualr to a uniform magnetic field and then spun around one of its sides at frequency f. The induced emf is a maximum when the
Flux is zero
Flux is maximum
Flux is half its maximum value
Derivative of the flux with respect to time is zero
The correct Answer is:A
To solve the problem, we need to analyze the situation of a rectangular loop of wire spinning in a uniform magnetic field and determine when the induced electromotive force (emf) is at its maximum.
1. Understanding the Setup:
- We have a rectangular loop of wire placed perpendicular to a uniform magnetic field.
- The loop is spun around one of its sides at a frequency f.
2. Magnetic Flux Calculation:
- The magnetic flux Φ through the loop is given by the formula:
Φ=B⋅A⋅cos(θ)
where:
- B is the magnetic field strength,
- A is the area of the loop,
- θ is the angle between the magnetic field and the normal (perpendicular) to the plane of the loop.
3. Initial Condition:
- Initially, when the loop is perpendicular to the magnetic field, θ=0 degrees. Thus, the magnetic flux is maximum:
Φmax=B⋅A⋅cos(0)=B⋅A
4. Rotation of the Loop:
- As the loop spins, the angle θ changes with time. If the loop spins with an angular velocity ω, then:
θ=ωt
- The magnetic flux at time t can then be expressed as:
Φ(t)=B⋅A⋅cos(ωt)
5. Induced EMF Calculation:
- According to Faraday's law of electromagnetic induction, the induced emf E is given by the negative rate of change of magnetic flux:
E=−dΦdt
- Substituting the expression for magnetic flux:
E=−ddt(B⋅A⋅cos(ωt))=B⋅A⋅ω⋅sin(ωt)
6. Finding Maximum Induced EMF:
- The induced emf is maximum when sin(ωt)=1. This occurs at:
ωt=π2+nπ(n∈Z)
- At this point, cos(ωt)=0, which means the magnetic flux Φ is zero.
7. Conclusion:
- Therefore, the induced emf is maximum when the magnetic flux through the loop is zero.
Final Answer:
The induced emf is maximum when the magnetic flux is zero.
---
- We have a rectangular loop of wire placed perpendicular to a uniform magnetic field.
- The loop is spun around one of its sides at a frequency f.
- The magnetic flux Φ through the loop is given by the formula:
Φ=B⋅A⋅cos(θ)
where:
- B is the magnetic field strength,
- A is the area of the loop,
- θ is the angle between the magnetic field and the normal (perpendicular) to the plane of the loop.
- Initially, when the loop is perpendicular to the magnetic field, θ=0 degrees. Thus, the magnetic flux is maximum:
Φmax=B⋅A⋅cos(0)=B⋅A
- As the loop spins, the angle θ changes with time. If the loop spins with an angular velocity ω, then:
θ=ωt
- The magnetic flux at time t can then be expressed as:
Φ(t)=B⋅A⋅cos(ωt)
- According to Faraday's law of electromagnetic induction, the induced emf E is given by the negative rate of change of magnetic flux:
E=−dΦdt
- Substituting the expression for magnetic flux:
E=−ddt(B⋅A⋅cos(ωt))=B⋅A⋅ω⋅sin(ωt)
- The induced emf is maximum when sin(ωt)=1. This occurs at:
ωt=π2+nπ(n∈Z)
- At this point, cos(ωt)=0, which means the magnetic flux Φ is zero.
- Therefore, the induced emf is maximum when the magnetic flux through the loop is zero.
The induced emf is maximum when the magnetic flux is zero.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - B)
22 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - C)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Try Yourself
42 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
Knowledge Check
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.
A rectangular coil is placed in a region having a uniform magnetic field B perpendicular to the plane of the coil. An emf will not be induced ion the coil if the

View SolutionA semicircular conducting wire of radius a is moving perpendicular to a uniform magnetic field B with speed√2vas shown in the figure.The emf induced across the wire Is
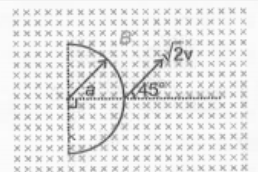
View SolutionA copper rod of length l is rotated about one end perpendicular to the uniform magnetic field B with constant angular velocity ω . The induced e.m.f. between its two ends is
View SolutionA metallic loop is placed in a non-uniform steady magnetic field. Will an emf be induced in the loop?
View SolutionA coil of metal wire is kept stationary in a non-uniform magnetic field. An e.m.f. Is induced in the coil.
View SolutionA coil of metal wire is kept stationary in a non-uniform magnetic field. An e.m.f. Is induced in the coil.
View SolutionA rectangular loop moving in a uniform magnetic equivalence of each branch. What is the net induced emf.

View Solution
