10 kJ/s of heat is produced when a DC flows through a resistor. Which of the following ac produces nearly same heat per sec through the same resistor ?
The correct Answer is:A
To solve the problem step by step, we need to determine the AC current that produces the same amount of heat per second in a 100 Ω resistor as the given DC current.
1. Understanding the Heat Produced by DC:
The heat produced (H) in a resistor when a current (I) flows through it for time (t) is given by the formula:
H=I2Rt
In this case, we are given that H=10kJ/s=10,000J/s and R=100Ω. Since we want to find the heat produced per second, we can set t=1s.
2. Substituting the Values:
We can rearrange the formula to solve for the current I:
10,000=I2×100×1
Simplifying this gives:
I2=10,000100=100
3. Calculating the DC Current:
Taking the square root of both sides, we find:
I=√100=10A
So, the DC current is 10 A.
4. Finding the Equivalent AC Current:
For AC, the effective (RMS) current Irms is related to the peak current I0 by the equation:
Irms=I0√2
Since we want the heat produced by AC to be the same as that produced by the DC current, we can set:
H=I2rmsRt
We already know H=10,000J/s and R=100Ω.
5. Setting Up the Equation for AC:
Substituting the known values into the equation:
10,000=I2rms×100×1
Rearranging gives:
I2rms=10,000100=100
6. Calculating the RMS Current:
Taking the square root:
Irms=√100=10A
7. Finding the Peak Current:
To find the peak current I0:
I0=Irms×√2=10×√2≈10×1.414=14.14A
8. Choosing the Closest Option:
The options provided are 15 A, 45 A, 30 A, and 10 A. The closest value to 14.14 A is 15 A.
Final Answer:
The AC current that produces nearly the same heat per second through the same resistor is approximately 15 A.
The heat produced (H) in a resistor when a current (I) flows through it for time (t) is given by the formula:
H=I2Rt
In this case, we are given that H=10kJ/s=10,000J/s and R=100Ω. Since we want to find the heat produced per second, we can set t=1s.
We can rearrange the formula to solve for the current I:
10,000=I2×100×1
Simplifying this gives:
I2=10,000100=100
Taking the square root of both sides, we find:
I=√100=10A
So, the DC current is 10 A.
For AC, the effective (RMS) current Irms is related to the peak current I0 by the equation:
Irms=I0√2
Since we want the heat produced by AC to be the same as that produced by the DC current, we can set:
H=I2rmsRt
We already know H=10,000J/s and R=100Ω.
Substituting the known values into the equation:
10,000=I2rms×100×1
Rearranging gives:
I2rms=10,000100=100
Taking the square root:
Irms=√100=10A
To find the peak current I0:
I0=Irms×√2=10×√2≈10×1.414=14.14A
The options provided are 15 A, 45 A, 30 A, and 10 A. The closest value to 14.14 A is 15 A.
The AC current that produces nearly the same heat per second through the same resistor is approximately 15 A.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - C ) (Objective Type Questions) ( More than one option are correct)2videos
ALTERNATING CURRENT
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - D) (Linked Comprehension Type Questions)3videos
ALTERNATING CURRENT
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - A) ( Objective Type Questions ( One option is correct))40videos
ALTERNATING CURRENT
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - ASSIGNMENT SECTION J (Aakash Challengers )5videos
ATOMS
Similar Questions
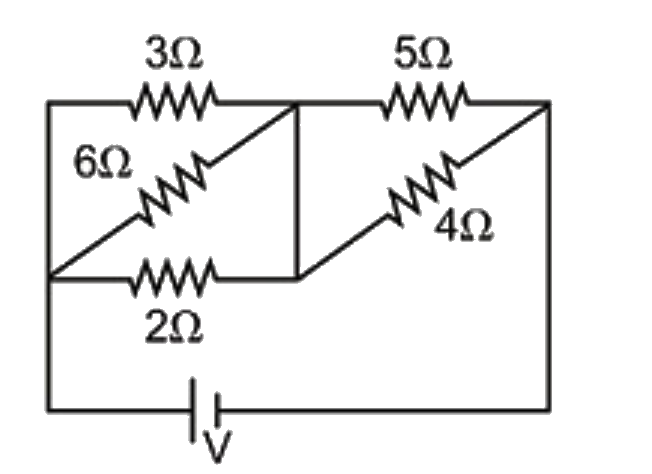
The current (in A) flowing through 6Ω resistor in the following circuit is:
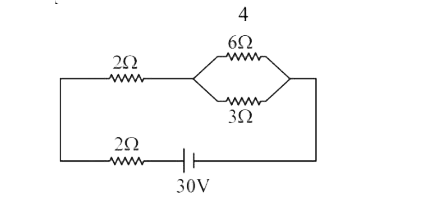 View Solution
View SolutionThe current (in A) flowing through 6Ω resistor in the following circuit is:
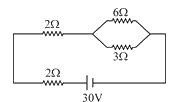 View Solution
View SolutionThe current I1 ( in A ) flowing through 1 Ω resistor in the following circuit is :
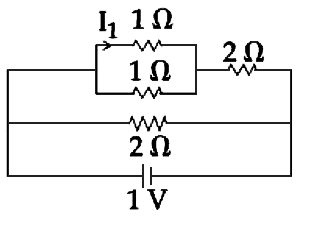 View Solution
View SolutionThe current I1 (in A) flowing through 3Ω resistor in the following circuit is:
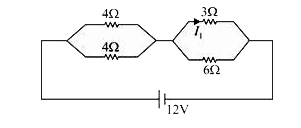 View Solution
View SolutionThe current I1 (in A) flowing through 3Ω resistor in the following circuit is:
 View Solution
View SolutionThe resistor in which maximum heat will be produced is
 View Solution
View SolutionResistors of 1, 2, 3 ohm are connected in the form of a triangle. If a 1.5V cell of negligible internal resistance is connected across 3 ohm resistor, the current flowing through this resistance will be
View SolutionWhat is the r.m.s. value of an alternating current which when passed through a resistor produces heat which is thrice of that produced by a direct current of 2 amperes in the same resistor?
View Solution100J of heat are produced each second in a 4Ω resistance. Find the potential difference across the resistor.
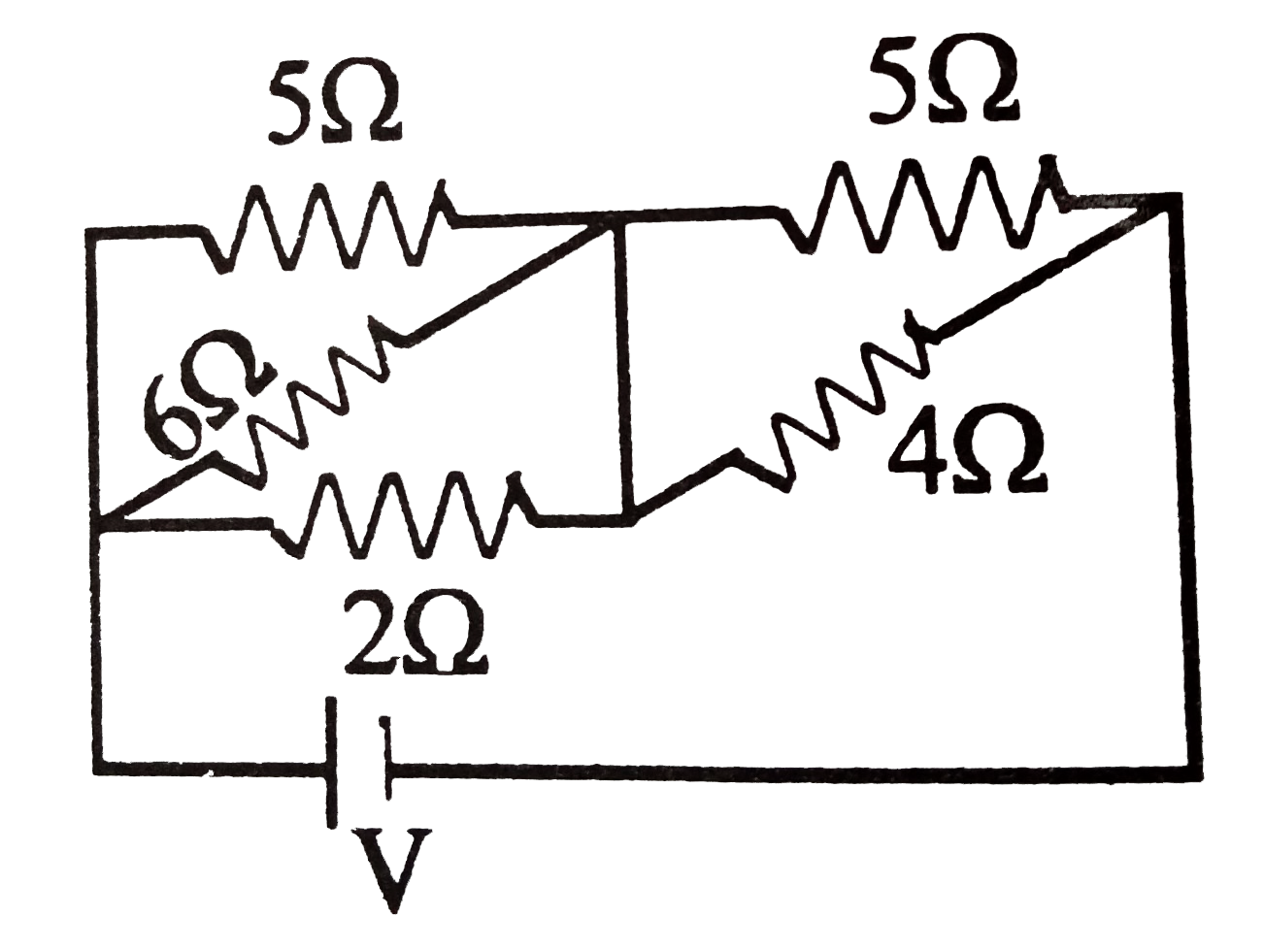
View SolutionFind the resistor in which maximum heat will be produced.
 View Solution
View Solution

