Three vessels containing same liquid, upto the same height h, then pressure at the bottom is (A1>A2>A3)
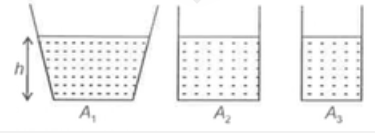
Maximum in A3
Same in all three cases
Maximum in A2
Maximum in A1
The correct Answer is:B
Step by step video & image solution for Three vessels containing same liquid, upto the same height h, then pressure at the bottom is (A_1 > A_2 > A_3) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In a cylindrical vessel containing liquid of density ρ there are two holes in the side walls at heights of h1 and h2 respectively such that the range of efflux at the bottom of the vessel is same. The height of a hole for which the range of efflux would be maximum, will be

View SolutionStatement I: In the three cases shown in the figure, force exerted by liquid on three vessels is the same.
Statement II: Pressure at the bottom in each case is same.

View Solution
Knowledge Check
Three vessels A,B,and C of different shapes contain a water upto the same height as shown in the figure .PA,PB ,and PC be the pressure exerted by the water at the bottom of the vessels A ,B and C respectively . Then
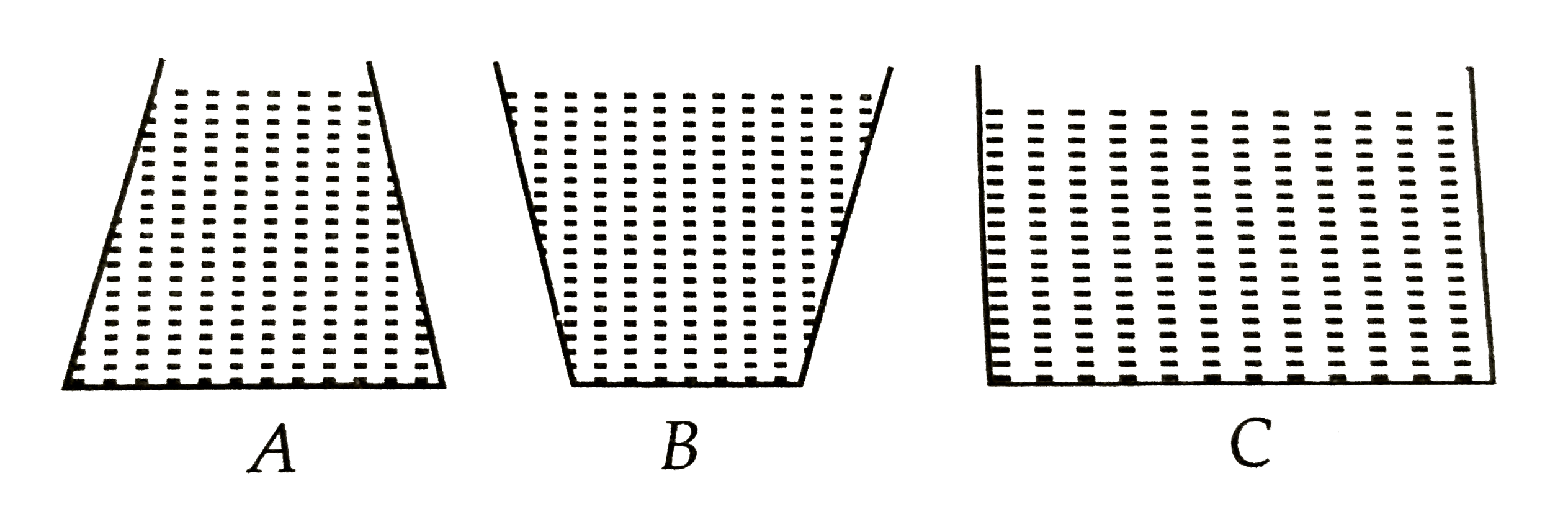 APA>PB>PCBPB>PC>PACPC>PB>PADPA=PB=PC
APA>PB>PCBPB>PC>PACPC>PB>PADPA=PB=PC
a1,a2,a3,∈R−{0} and a1+a2cos2x+a3sin2x=0forallx∈R, then (a)vector →a=a1ˆi+a2ˆj+a3ˆkand→b=4ˆi+2ˆj+ˆk are perpendicular to each other (b)vector →a=a1ˆi+a2ˆj+a3ˆkand→b=−ˆi+ˆj+2ˆk are parallel to each other (c)vector →a=a1ˆi+a2ˆj+a3ˆk is of length√6 units, then one of the ordered triple (a1,a2,a3)=(1,−1,−2) (d)are perpendicular to each other if 2a1+3a2+6a3=26,then∣∣a1ˆi+a2ˆj+a3ˆk∣∣is2√6
View SolutionIn a four-dimensional space where unit vectors along the axes are ˆi,ˆj,ˆk and ˆl, and →a1,→a2,→a3,→a4 are four non-zero vectors such that no vector can be expressed as a linear combination of others and (λ−1)(→a1−→a2)+μ(→a2+→a3)+γ(→a3+→a4−2→a2)+→a3+δ→a4=0, then
View SolutionIf a1,a2,a3,a4 be the coefficient of four consecutive terms in the expansion of (1+x)n, then prove that: a1a1+a2+a3a3+a4=2a2a2+a3.
View SolutionIf a1,a2,a3,a4 be the coefficient of four consecutive terms in the expansion of (1+x)n, then prove that: a1a1+a2+a3a3+a4=2a2a2+a3.
View SolutionFind the number of all three elements subsets of the set{a1,a2,a3,an} which contain a3.
View SolutionFind the number of ways of arranging 15 students A1,A2,........A15 in a row such that (i) A2, must be seated after A1andA2, must come after A2 (ii) neither A2 nor A3 seated brfore A1
View SolutionIf (b2−b1)(b3−b1)+(a2−a1)(a3−a1)=0, then prove that the circumcenter of the triangle having vertices (a1,b1),(a2,b2) and (a3,b3) is (a2+a32,b2+b32).
View Solution
