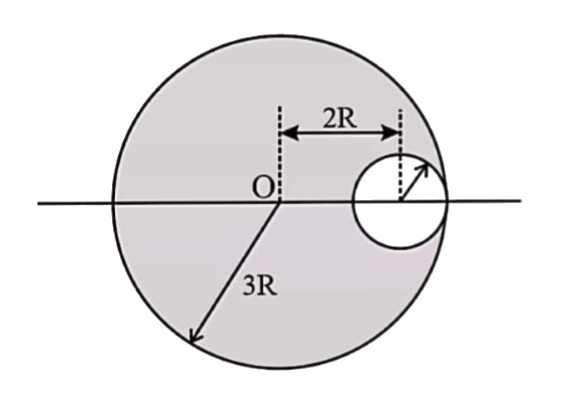
A uniform circular disc of radius R and weight 90 N is shown in figure. If a small circular portion is cut out, then coordinates of new centre of mass will be (Remaining weight of disc is 65 N and y = 3R5)
(3R13,0)
(−3R13,0)
(0,3R13)
(0,−3R13)
Step by step video & image solution for A uniform circular disc of radius R and weight 90 N is shown in figure. If a small circular portion is cut out, then coordinates of new centre of mass will be (Remaining weight of disc is 65 N and y = frac{3R}{5}) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A uniform circular disc has a radius of 20cm. A circular disc of radius 10cm is cut concentrically from the original disc. The shift in centre of mass is
View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −

View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is

View SolutionThe figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is
View SolutionA uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),

View SolutionFrom a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :

View SolutionFigure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is R/2. Find the centre of mass of the remaining part of the disc.

View SolutionA circular metallic disc of radius R has a small circular cavity of radius r as shown in figure. On heating the system

View SolutionFrom a uniform circular disc of mass M and radius R a small circular disc of radius R/2 is removed in such a way that both have a common tangent. Find the distance of centre of mass of remaining part from the centre of original disc.
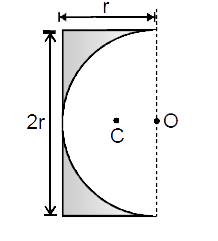
View SolutionA semicircular portion of radius 'r' is cut from a uniform rectangular plate as shown in figure. The distance of centre of mass 'C' of remaining plate, from point 'O' is
View Solution
