Given M is the mid-point of AB, find the co-ordinates of:
A, if M = (1, 7) and B = (-5, 10),
To find the coordinates of point A given that M is the midpoint of line segment AB, we can use the midpoint formula. The midpoint M of a line segment with endpoints A(x1, y1) and B(x2, y2) is given by:
M=(x1+x22,y1+y22)
1. Identify the given values:
- Midpoint M = (1, 7)
- Point B = (-5, 10)
- Let the coordinates of point A be (x1, y1).
2. Set up the equations using the midpoint formula:
- For the x-coordinate:
1=x1+(−5)2
- For the y-coordinate:
7=y1+102
3. Solve the x-coordinate equation:
- Multiply both sides by 2:
2=x1−5
- Add 5 to both sides:
x1=2+5=7
4. Solve the y-coordinate equation:
- Multiply both sides by 2:
14=y1+10
- Subtract 10 from both sides:
y1=14−10=4
5. Write the coordinates of point A:
- Therefore, the coordinates of point A are (7, 4).
Final Answer:
The coordinates of point A are (7, 4).
- Midpoint M = (1, 7)
- Point B = (-5, 10)
- Let the coordinates of point A be (x1, y1).
- For the x-coordinate:
1=x1+(−5)2
- For the y-coordinate:
7=y1+102
- Multiply both sides by 2:
2=x1−5
- Add 5 to both sides:
x1=2+5=7
- Multiply both sides by 2:
14=y1+10
- Subtract 10 from both sides:
y1=14−10=4
- Therefore, the coordinates of point A are (7, 4).
The coordinates of point A are (7, 4).
Topper's Solved these Questions
- SECTION AND MID-POINT FORMULABOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - EXERCISE 13 (C)
28 Videos
- SECTION AND MID-POINT FORMULABOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - QUESTIONS
17 Videos
- SECTION AND MID-POINT FORMULABOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - QUESTIONS
17 Videos
- SAMPLE PAPER 5 (MATHEMATICS)BOOK - ICSECHAPTER - SAMPLE PAPER 5 (MATHEMATICS)EXERCISE - SECTION C
8 Videos
- SHARES AND DIVIDENDSBOOK - ICSECHAPTER - SHARES AND DIVIDENDSEXERCISE - Exercise 3(C )
20 Videos
Similar Questions
Given M is the mid-point of AB, find the co-ordinates of:
B, if A = (3,-1) and M = (-1, 3).
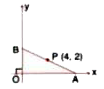
View SolutionIn the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the

co-ordinates of A and B.
View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
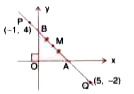
The co-ordinates of A and B.
View SolutionA (5, 3), B (-1, 1) and C (7, -3) are the vertices of triangle ABC. If L is the mid-point of AB and M is the mid-point of AC, show
that : LM=12BC.
View SolutionA(-2,4),C(4,10) and D(-2,10) are the vertices of a square ABCD. Use the graphical method to find the co-ordinates of the fouth vertex B. Find :
(i) the co-ordinates of the mid point of BC
(ii) the co-ordinates of the mix point of CD and
(iii) the co-ordinates of the point of intersection of the diagonals of the square ABCD.
View SolutionThe base QR of an equilateral triangle PQR lies on X-axis. The co-ordinates of the point Q are (-4,0) and origin is the mid-point of the base. Find the co-ordinates of the points P and R.
View SolutionIn the adjoining figure
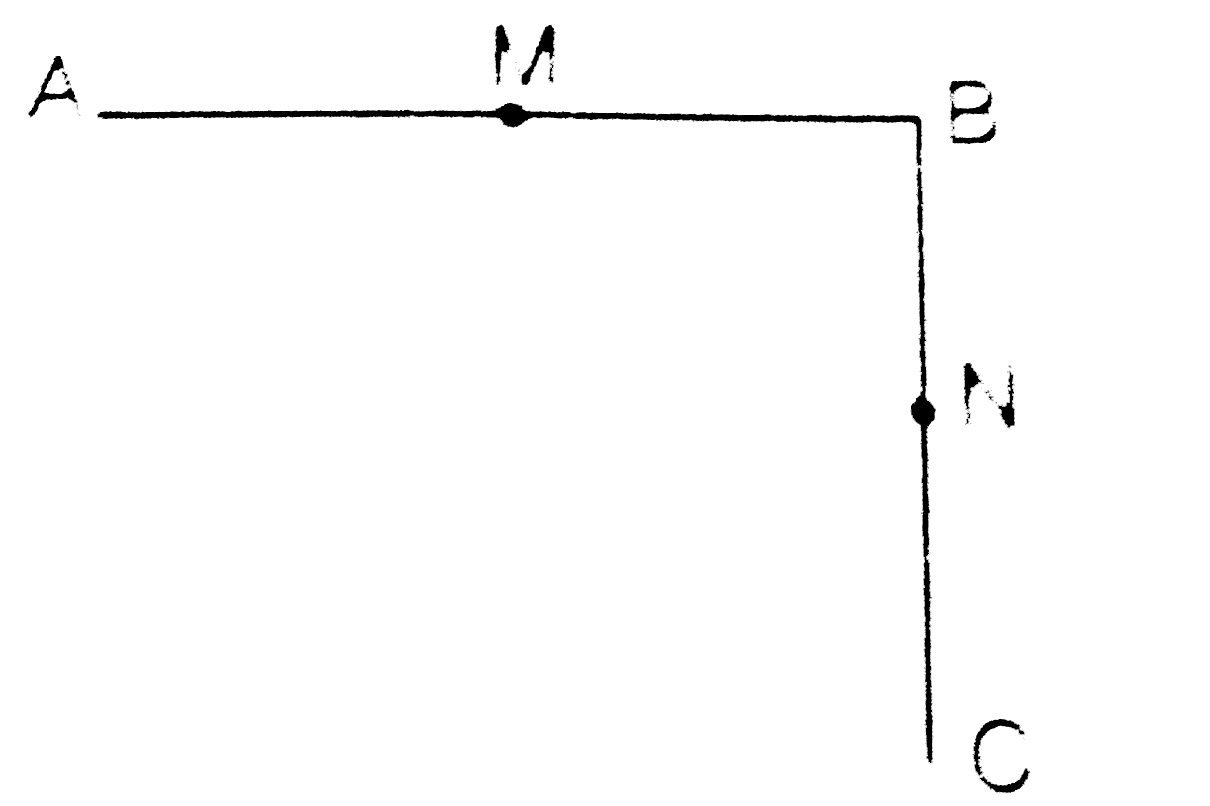
(i) AB=BC, M is the mid -point of AB and N is the mid- point of BC. Show that AM=NC.
(ii) BM=BN,M is the mid- point of AB and N is the mid - point of BC. Show that AB=BC.
View SolutionThe line 4x + 5y + 20 = 0 meets x-axis at point A and y-axis at point B Find :
the co-ordinates of point P in AB such that AB : BP = 5:3.
View SolutionM is point on AB extended such that 3.AM = 7. BM. The co-ordinates of A and M are (3,0) and ( - 4,7) respectively . What are the co-ordinates of B ?
View Solution
