ABC is an isosceles trianlge with AB=AC. A circle through B touches side AC at its middle point D and intersects side AB in point P. Show that AB=4×AP.
The correct Answer is:AB=4×AP
To solve the problem, we will follow these steps:
Step 1: Draw the Isosceles Triangle
Draw triangle ABC such that AB = AC. Mark the midpoint of AC as point D.
Step 2: Draw the Circle
Draw a circle that passes through point B and touches side AC at point D.
Step 3: Identify the Tangent and Secant
Recognize that line segment AD is the tangent to the circle at point D, and line segment AB is the secant that intersects the circle at point P.
Step 4: Apply the Tangent-Secant Theorem
According to the tangent-secant theorem, we have:
AD2=AP⋅AB
where:
- AD is the length of the tangent segment,
- AP is the length of the exterior portion of the secant,
- AB is the length of the whole secant.
Step 5: Express AD in Terms of AB
Since D is the midpoint of AC, we have:
AD=AC2=AB2
because AB = AC in an isosceles triangle.
Step 6: Substitute AD in the Equation
Substituting AD in the tangent-secant theorem gives us:
(AB2)2=AP⋅AB
Step 7: Simplify the Equation
This simplifies to:
AB24=AP⋅AB
Step 8: Solve for AB
Dividing both sides by AB (assuming AB ≠ 0) gives:
AB4=AP
Thus, we can express AB as:
AB=4⋅AP
Conclusion
We have shown that:
AB=4⋅AP
---
Draw triangle ABC such that AB = AC. Mark the midpoint of AC as point D.
Draw a circle that passes through point B and touches side AC at point D.
Recognize that line segment AD is the tangent to the circle at point D, and line segment AB is the secant that intersects the circle at point P.
According to the tangent-secant theorem, we have:
AD2=AP⋅AB
where:
- AD is the length of the tangent segment,
- AP is the length of the exterior portion of the secant,
- AB is the length of the whole secant.
Since D is the midpoint of AC, we have:
AD=AC2=AB2
because AB = AC in an isosceles triangle.
Substituting AD in the tangent-secant theorem gives us:
(AB2)2=AP⋅AB
This simplifies to:
AB24=AP⋅AB
Dividing both sides by AB (assuming AB ≠ 0) gives:
AB4=AP
Thus, we can express AB as:
AB=4⋅AP
We have shown that:
AB=4⋅AP
Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18(A)
24 Videos
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (B)
18 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)BOOK - ICSECHAPTER - SPECIMEN QUESTION PAPER (MATHEMATICS)EXERCISE - Section C
12 Videos
- TRIGONOMETRICAL IDENTITIESBOOK - ICSECHAPTER - TRIGONOMETRICAL IDENTITIESEXERCISE - QUESTIONS
22 Videos
Similar Questions
ABC is an isosceles triangle with AB =AC and BD,CE are its two medians. Show that BD=CE .
View SolutionThe incircle of an isoceles triangle ABC, with AB=AC, touches the sides AB,BC and CA at D,E and F respecrively. Prove that E bisects BC.
View SolutionIf ΔABC is an isosceles triangle with AB = AC. Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
View SolutionLet triangle ABC be an isosceles with AB=AC. Suppose that the angle bisector of its angle B meets the side AC at a point D and that BC=BD+AD. Measure of the angle A in degrees, is :
View SolutionABC is a right triangle, right - angled at the vertex A. A circle is drawn to touch the sides AB and AC at points P and Q respectively such that the other end points of the diameters passing through P and Q lie on the side BC. IF AB = 6 units, then the area (in sq. units) of the circular sector which lies inside the triangle is
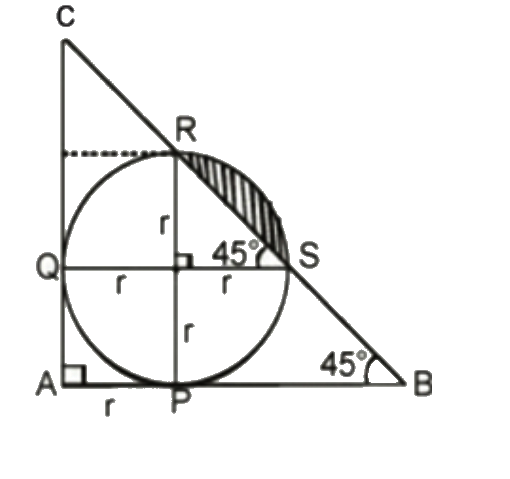
View SolutionAB is the diameter and AC is a chord of a circle with centre O such that angle BAC=30∘. The tangent to the circle at C intersects AB produced in D. Show that BC=BD.
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionD is a point in side BC of triangle ABC. If AD>AC, show that AB>AC.
View SolutionIf D any point on the BC of an isosceles triangle ABC then prove that AB>AD and AC>AD.
View Solution
