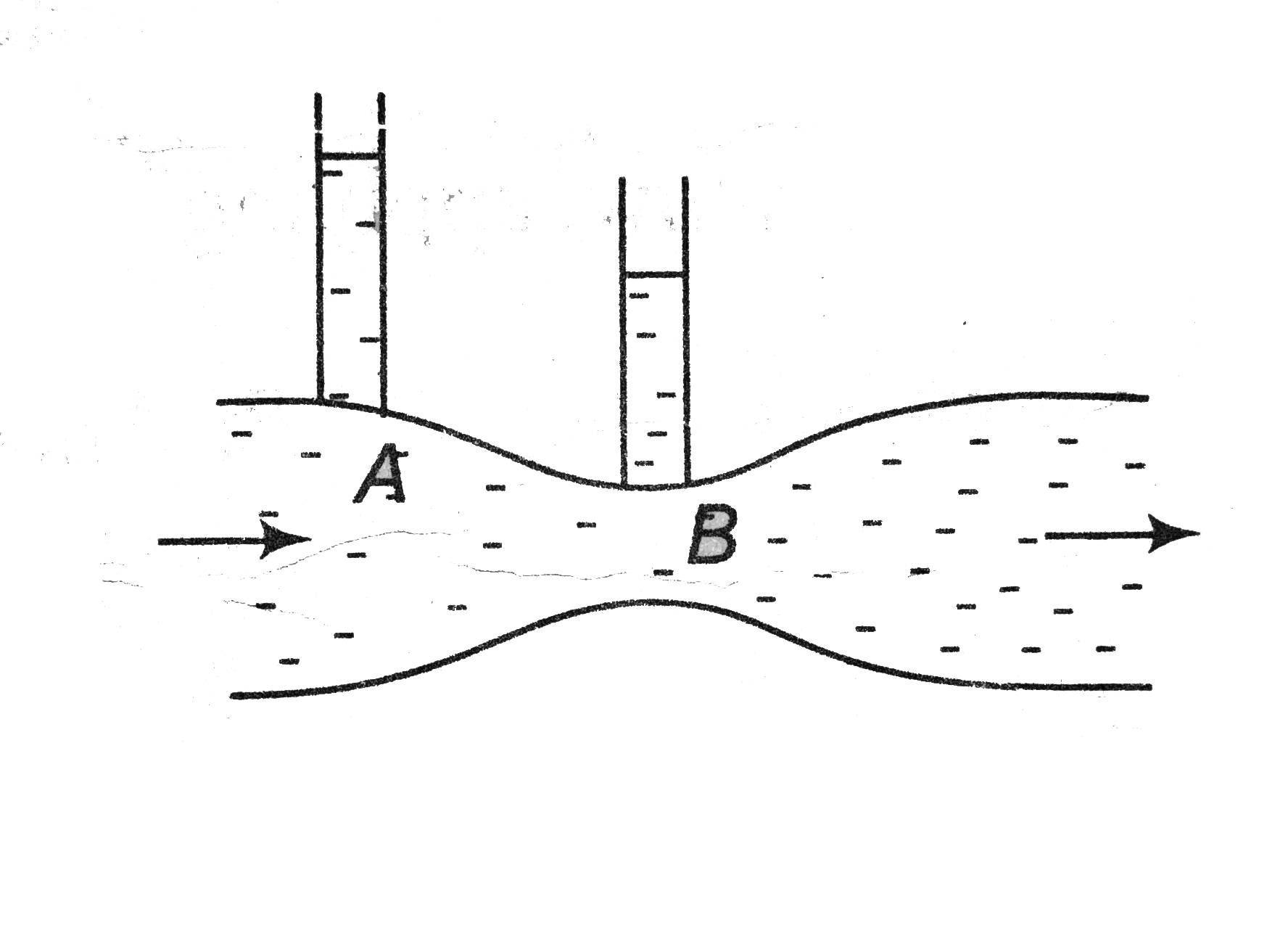
Water flows in a horizontal tube as shown in figure. The pressure of water changes by 600 N m^-2 between A and B where the areas of cross section are 30cm^2 and 15cm^2 respectively. Find the rate of flow of water through the tube.
,

Video Solution

Text Solution

Verified by Experts

Let the velocity at $x = v_{x}$ and that at $y = v_{y}$ .
By the equation of continuity, $\frac{v_{y}}{v_{x}} = \frac{3 c m^{2}}{1.5 c m^{2}} = 2$ .
By Bernoulli's equation,
$P_{x} + \frac{1}{2} ρ v_{x}^{2} = P_{y} + \frac{1}{2} ρ v_{y}^{2}$ or, $P_{x} - P_{y} = \frac{1}{2} ρ {(2 V_{y})}_{y}^{2} - \frac{1}{2} ρ v_{y}^{2} = \frac{3}{2} ρ V_{y}^{2}$
or, $600 \frac{N}{m^{2}} = \frac{3}{2} (1000 \frac{k g}{m^{3}}) v_{x}^{2}$
or, $v_{x} = \sqrt{0.4 m^{2} / s^{2}} = 0.63 m / s$ .
The rate of flow $= (3 c m^{2}) (0.63 m / s) = 189 c m^{3} / s$ .