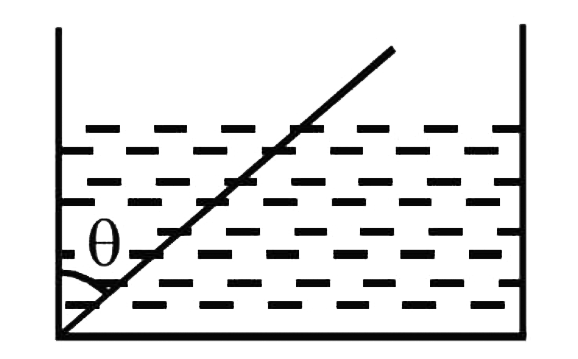
The wooden plank of length 1 m and uniform cross section is hinged at one end to the bottom of a tank as shown in figure. The tank is filled with water up to a height of 0.5 m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=0)
 ,
,
The force acting on the plank are shown in the figure. The height of water level is l. The length of the plank is 2l. The weight of the plank acts through the centre B of the plank.
We have OB=l. The buoyant force F acts though the point A which is the middle point of the dippeed part OC of the plank. We have OA=OC2=l2cosθ
Let the mass per unit length of the plank be ρ.
Its weight mg=2lρg.
The mass of the part OC of the plank =(lcosθ)ρ.
The mass of water displaced =10.5lcosθρ=2lρcosθ
The buoyant force F is, therefore, F=2lρgcosθ.
Now, for equilibrium, the torque of mg about O should balance the torque of F about O.
So, mg(OB)sinθ=F(OA)sinθ
or, (2lρ)l=(2lρcosθ)(l2cosθ) or, cos2θ=12 or, cosθ=1√2
or, θ=45∘.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Board Level Exercise18videos
FLUID MECHANICS
- BOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise- 1 PART - I Section (A)3videos
FLUID MECHANICS
- BOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Advanced Level Problems8videos
FLUID MECHANICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise52videos
ELECTROSTATICS
- BOOK - RESONANCE ENGLISHCHAPTER - FULL TEST 1EXERCISE - Exercise30videos
FULL TEST 1
Similar Questions
A wooden plank of length 1m and uniform cross-section is hinged at one end to the bottom of a tank as shown in fig. The tank is filled with water upto a hight 0.5m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=θ∘)
 View Solution
View SolutionA wooden rod of a uniform cross section and of length 120cm is hinged at the bottom of the tank which is filled with water to a height of 40cm. In the equilibrium position, the rod makes an angle of 60∘ with the vertical. The centre of buoyancy is located on the rod at a distance (from the hinge) of
View Solution
Knowledge Check
- Question 1 - Select One
A liquid of density ρ0 is filled in a wide tank to a height h. A solid rod of length L, cross-section A and density ρ is suspended freely in the tank. The lower end of the rod touches the base of the tank and h=L/n (where n gt 1). Then the angle of inclination θ of the rod with the horizontal in equilibrium position is
Asin−1(√ρ0ρ)Bsin−1(n√ρ0ρ)Csin−1(1n√ρ0ρ)Dsin−1(1n√ρρ0)
A tank of square cross section (2m×2m) is filled with water up to a height of 2.5m. Find the thrust experienced by the vertical and botom of the tank (g=10m/s2).
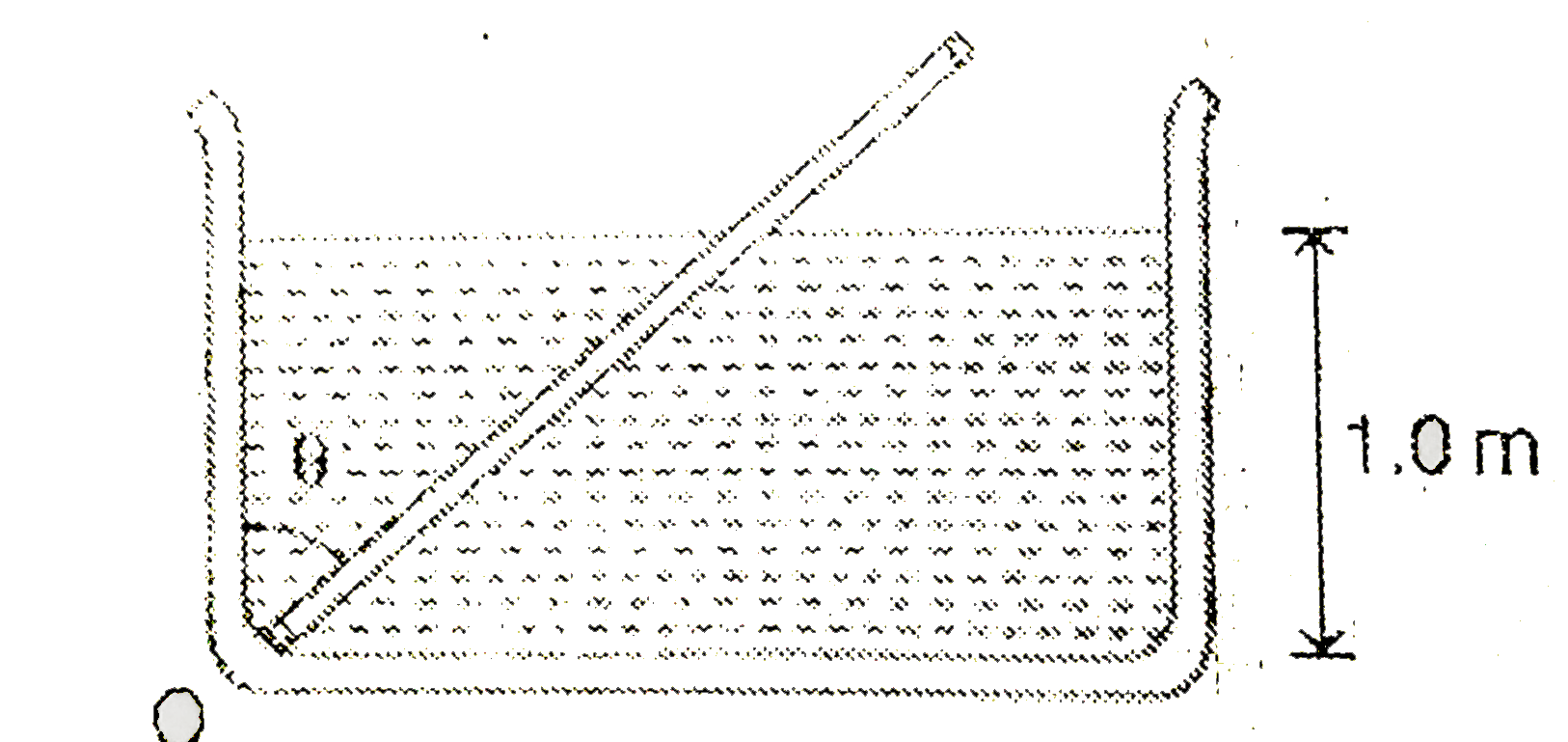
View SolutionA uniform rod of length 2.0 m specific gravity 0.5 and mass 2 kg is hinged at one end to the bottom of a tank of water (specific gravity = 10) filled upto a height o f 1.0 m as shown in figure. Taking the case θ=−0∘ the force exerted by the hings on the rod is (g=10m/s2)
 View Solution
View SolutionA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

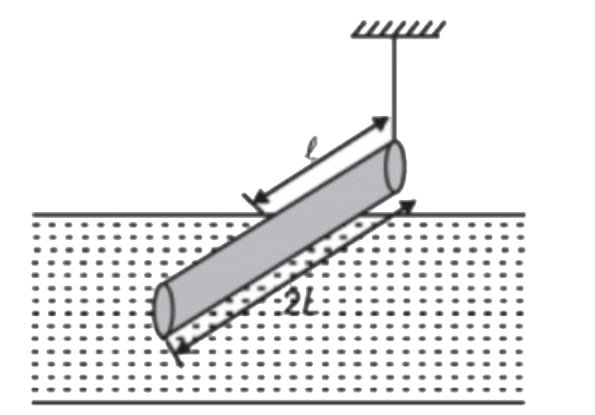
Find the angle 0 if the density of the material of the rod is half of the density of water.View SolutionA slender homogeneous rod of length 2L floats partly immersed in water, being supported by a string fastened to one of its ends, as shown in the figure. The specific gravity of the rod is 0.36. The length of the rod that extends out of the water is KL10 Find the value of K.
 View Solution
View SolutionA uniform wooden bar of length l and mass m hinged on a vertical wall of a containing water, at one end.

3/5th part of the bar is submerged in water. Find the ratio of densities of the liquid and the bar.View SolutionA tank 5 m high is half filled with water and then is filled to top with oil of density 0.85g/cm3 The pressure at the bottom of the tank, due to these liquids is
View Solution_S01_067_Q01.png)
A solid right cylinder of length l stands upright at rest on the bottom of a large tub filled with water up to height h as shown in the figure-I density of material of the cylinder equals to that of water. Now the cylinder is pulled slowly out of water with the help of a thin light inextensible thread as shown in figure-II. Find the work done by the tension force develop in the thread.
(a). mgh
(b). mgl
(c). 0.5 mgl
(d). mg(0.5l+h)View Solution

