A large block of ice 5m thick has a vertical hole drilled through it and is floating in the middle of a lake. What is the minimum length of a rope required to scoop up a bucket full of water through the hole? Relative density of ice =0.9.
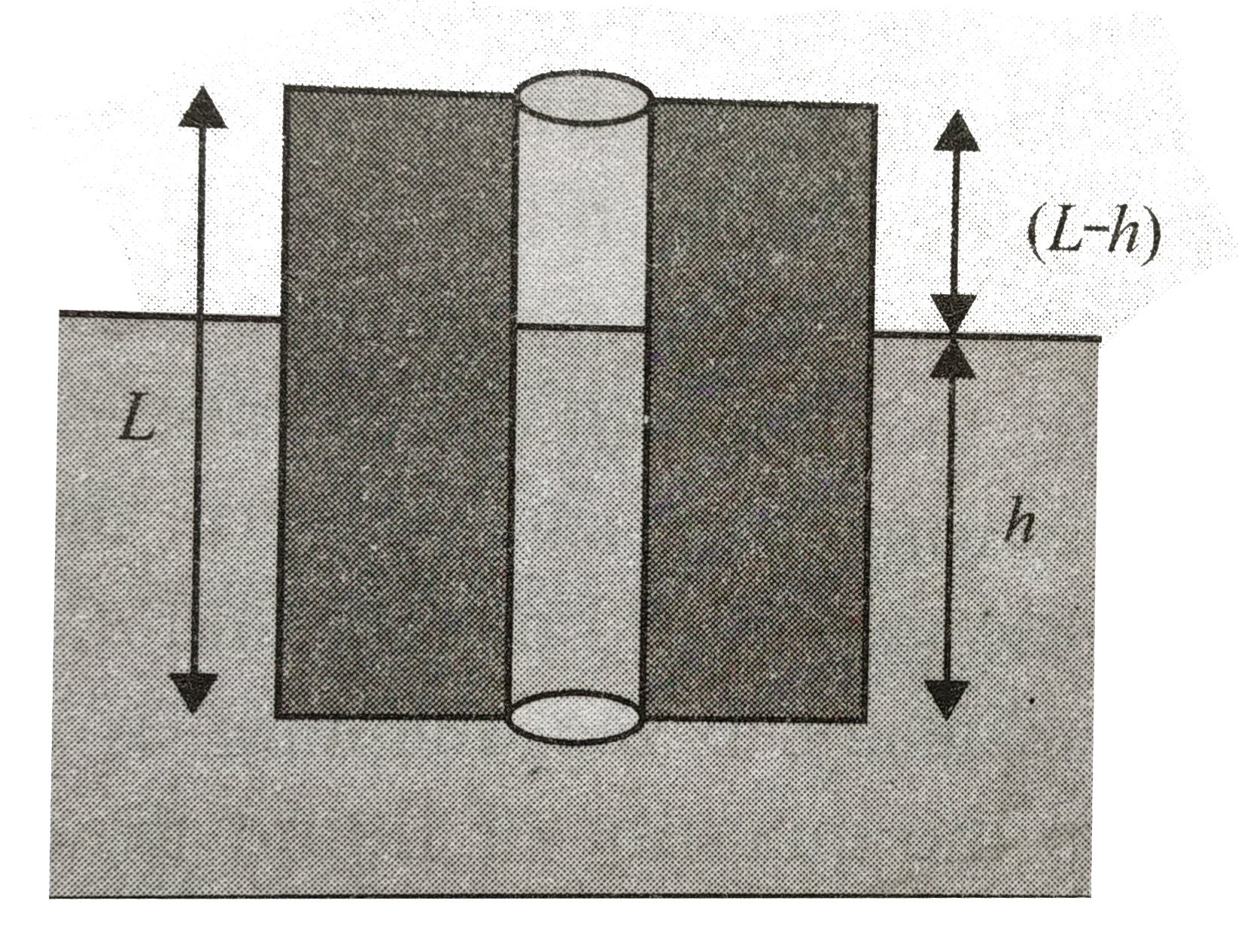
Let area of ice-cuboid excluding hole =A
weight of ice block = weight of liquid displaced Aρicelg=Aρw(l−h)g
9l10=l−h⇒h=l−9l10=(l10)

Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Board Level Exercise18videos
FLUID MECHANICS
- BOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise- 1 PART - I Section (A)3videos
FLUID MECHANICS
- BOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Advanced Level Problems8videos
FLUID MECHANICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise52videos
ELECTROSTATICS
- BOOK - RESONANCE ENGLISHCHAPTER - FULL TEST 1EXERCISE - Exercise30videos
FULL TEST 1
Similar Questions
A large block of ice 10 cm thick with a vertical hole drilled through it is floating in a lake. The minimum length of the rope required to scoop out a bucket full of water through the hole is (0.2x)m. Find the value of x. Take density of ice =0.9 g/cm3
View SolutionA large block of ice 10 cm thick with a vertical hole drilled through it is floating in a lake. The minimum of water through the hole is (density of ice =0.9gcm−3)
View SolutionA cubical block of ice floating in water has to support a metal piece weighing 0.5 kg. What can be the minimum edge of the block so that it does not sink in water? specific gravity of ice=0.9.
View SolutionA cubical block of ice floating in water has to suport metal piece weighing 0.5 kg. What can be the minimum edge of the block so that it does not sink in water/ specific gravity of ice=0.9.
View Solution
The figure above shows a metal triangular solid with two equilateral triangle faces and a thickness of 2 cm. The length of each side of a triangular face is 4 cm. A hole with a diameter of 1 cm is drilled through the solid. The density of the metal is 6 grams per cubic centimeter . What is the mass of this solid to the nearest gram ? (Density is mass divided by volume ).View SolutionA block of ice of total area A and thicknes 0.5m is floating in water. In order to just support a man of nass 100kg, the area A should be (the specific gravity of ice is 0.9)
View SolutionIn giving a patient blood transfusion the bottle is set up so that the level of blood is 1.3 m above the needle which has an internal diameter of 0-36 mm, and is 0-03 m in length. If 4-5 ce of blood passes through the needle in one minute calculate the viscosity of blood if density is 1020kgm−3
View SolutionTwo blocks of mass m1=10kg and m2=5kg connected to each other by a massless inextensible string of length 0.3m are placed along a diameter of the turntable. The coefficient of friction between the table and m1 is 0.5 while there is no friction between m2 and the table. the table is rotating with an angular velocity of 10rad/s. about a vertical axis passing through its center O. the masses are placed along the diameter of the table on either side of the center O such that the mass m1 is at a distance of 0.124m from O. the masses are observed to be at a rest with respect to an observed on the tuntable (g=9.8m/s2).
(a) Calculate the friction on m1
(b) What should be the minimum angular speed of the turntable so that the masses will slip from this position?
(c ) How should the masses be placed with the string remaining taut so that there is no friction on m1.View SolutionA bucket full of water weighs 5 kg, it is pulled from a well 20 m deep. There is a small hole in the bucket through which water leaks at a constant rate. If it is observed that for every meter the bucket loses 0.2 kg mass of water, then the total work done in pulling the bucket up from the well is [g=10ms−2]
View SolutionA pond has a layer of ice of thickness 0.25 m on its surface the temperature of the atmosphere is 10∘C. Find out the time required to increase the thickness of the layer of ice 0.5mm. K of ice =2Wm−2K−1. Density of ice =900kg m−3 latent heat of fusion of ice =336KJ kg−1.
View Solution

