Question

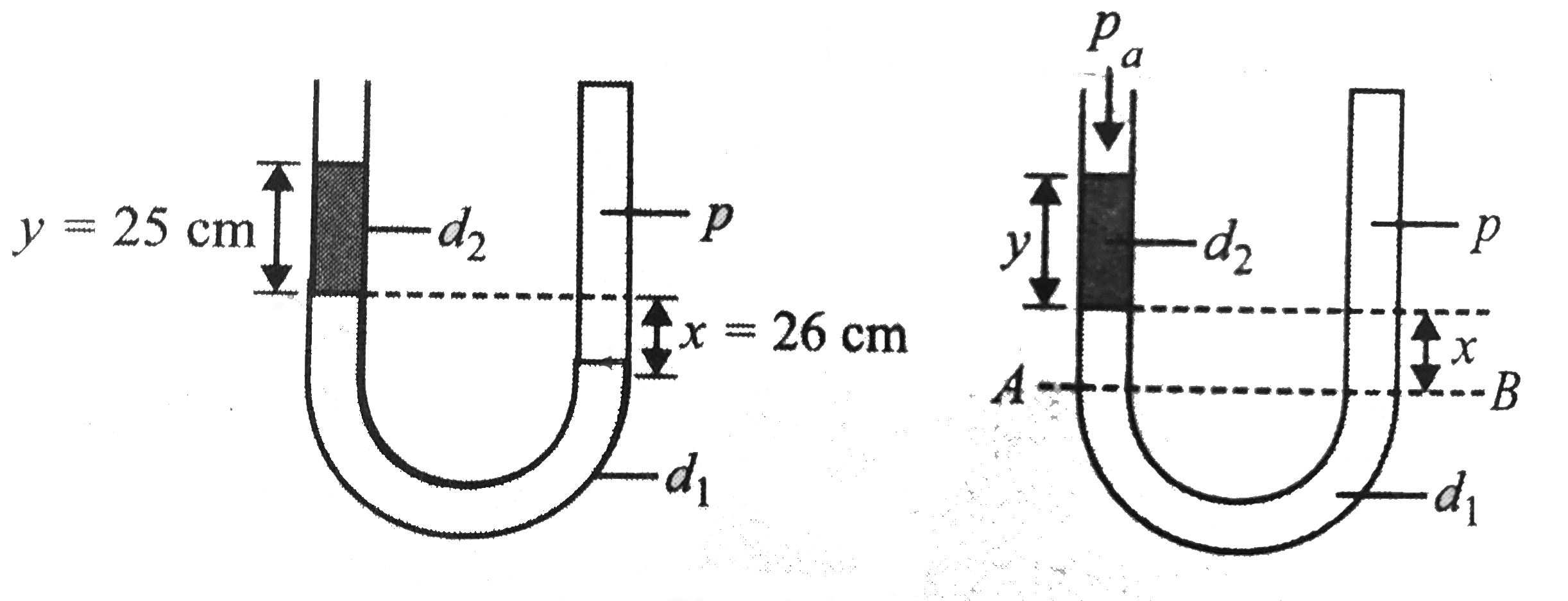
In a given U-tube (open at one-end) find out relation between p and $p_a$
Given $d_2=2\times 13.6gm/c{m}^3,d_1=13.6gm/c{m}^3$

Explanation

Pressure in a liquid at same level is same i.e., at `A - A-`,
`P_(a) + d_(2)yg + xd_(1)g = P`

In C.G.S.
`P_(a) + 13.6 xx 2 xx 25 xx g + 13.6 xx 26 xx g = P`
`P_(a) + 13.6 xx g [50 + 26] = P`
`2P_(a) = P [P_(a) = 13.6 xx g xx 76]`