For a particle performing SHM
The kinetic energy is never equal to the potential energy
the kinetic energy is always equal to the potential energy
The average kinetic in one time period is equal to the average potential in this period
The avarage kinetic energy in any time interval is equal to average potential energy in that interval.
The correct Answer is:C
To solve the problem regarding a particle performing Simple Harmonic Motion (SHM) and to identify the correct statements from the given options, we can follow these steps:
1. Understanding the Basics of SHM:
- In SHM, a particle oscillates back and forth around an equilibrium position. The motion can be described in terms of kinetic energy (KE) and potential energy (PE).
2. Analyzing the Statements:
- We need to evaluate each statement provided in the question.
3. Statement A: "The kinetic energy is never equal to the potential energy."
- This statement is incorrect. In SHM, there are instances where the kinetic energy can equal the potential energy, particularly when the particle is at the midpoint of its motion.
4. Statement B: "The kinetic energy is always equal to the potential energy."
- This statement is also incorrect. While kinetic energy can equal potential energy at certain points, it does not hold true for all positions in SHM.
5. Statement C: "The average kinetic energy in one period is equal to the average potential energy in that period."
- This statement is correct. Over one complete cycle of SHM, the average kinetic energy is equal to the average potential energy due to the conservation of mechanical energy.
6. Statement D: "The average kinetic energy in any interval of time is equal to the average potential energy in that interval."
- This statement is incorrect. The averages may not be equal in arbitrary intervals of time, as they depend on the specific positions and velocities of the particle during that interval.
7. Conclusion:
- After evaluating all statements, the only correct statement is Statement C.
Final Answer:
The correct option is C.
---
- In SHM, a particle oscillates back and forth around an equilibrium position. The motion can be described in terms of kinetic energy (KE) and potential energy (PE).
- We need to evaluate each statement provided in the question.
- This statement is incorrect. In SHM, there are instances where the kinetic energy can equal the potential energy, particularly when the particle is at the midpoint of its motion.
- This statement is also incorrect. While kinetic energy can equal potential energy at certain points, it does not hold true for all positions in SHM.
- This statement is correct. Over one complete cycle of SHM, the average kinetic energy is equal to the average potential energy due to the conservation of mechanical energy.
- This statement is incorrect. The averages may not be equal in arbitrary intervals of time, as they depend on the specific positions and velocities of the particle during that interval.
- After evaluating all statements, the only correct statement is Statement C.
The correct option is C.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - I
26 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - II
1 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - I
25 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
Similar Questions
Ratio of kinetic energy at mean position to potential energy at A/2 of a particle performing SHM
View SolutionThe figure shows a graph between velocity and displacement (from mean position) of a particle performing SHM:
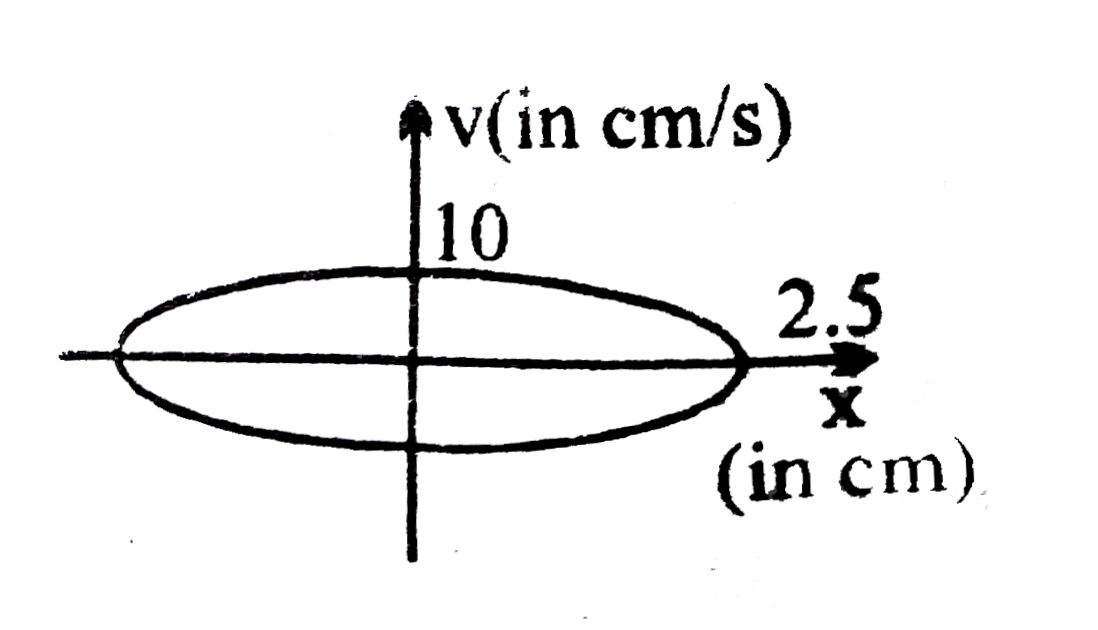
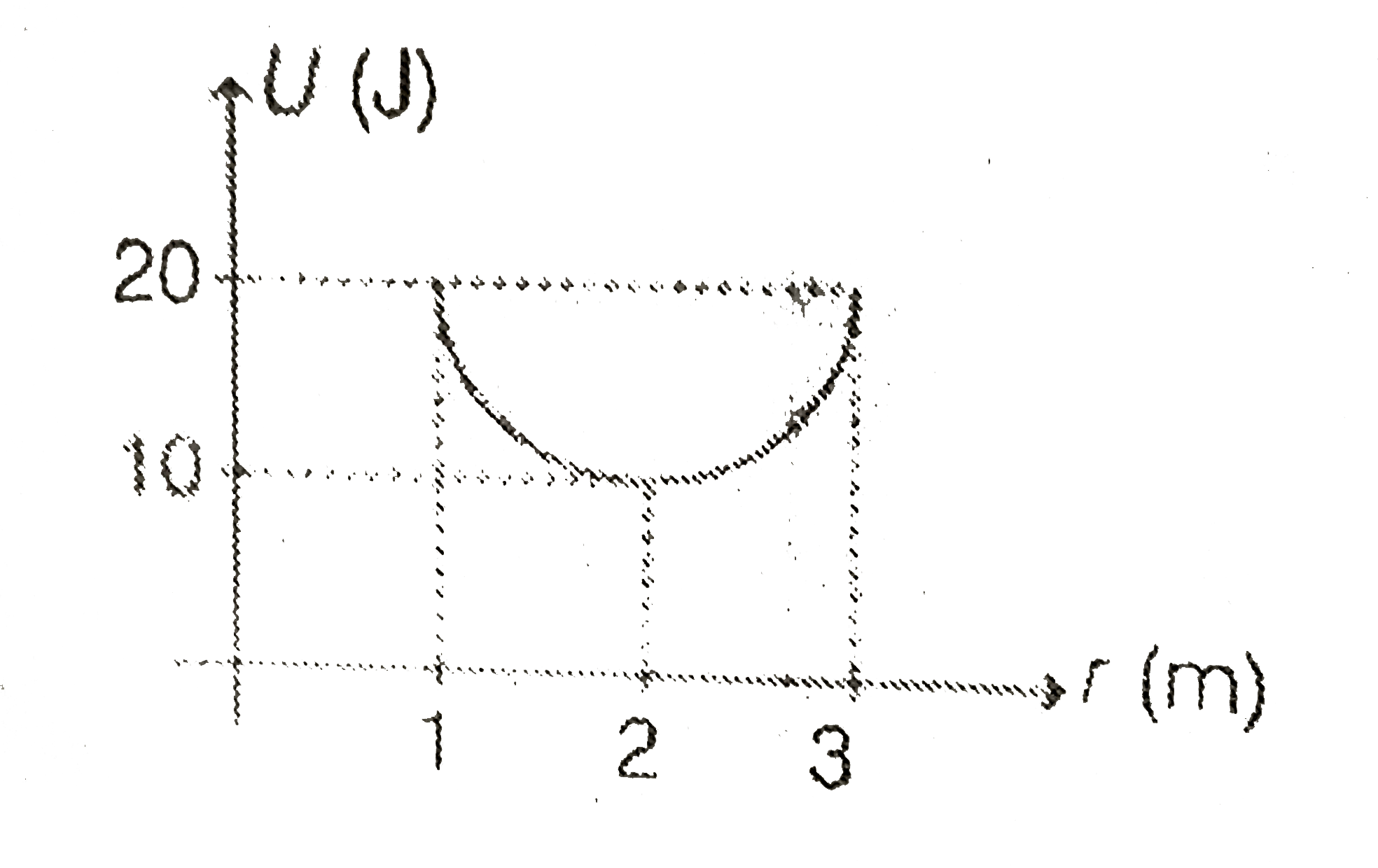
View SolutionU.r graph of a particle performing SHM is as shown in figure. What conclusion cannot be drawn from the graph?
View SolutionAt two particular closest instant of time t1 and t2 the displacements of a particle performing SHM are equal. At these instant
View SolutionAssume x=2cos(πt+π3) cm represents the position of a particle performing SHM. The initial position of particle on x-axis is
View SolutionThe acceleration of a particle performing SHM is12cm/s2 at a distance of 3 cm from the mean position . Calculate its time - period .
Hint :a=ω2x
a=12cm/s2,x=3cm
Find ω
T=πω
View SolutionThe total energy of particle performing SHM depend on : -
View SolutionAssertion : A particle performing SHM at certain instant is having velocity v. It again acquire a velocity v for the first time after a time interval of T second. Then the time period of oscillation is T second.
Reason : A particle performing SHM can have same velocity at two instants in one cycle.
View SolutionThe time taken by a particle performing SHM to pass from point A and B where it is velocities are same is 2s. After another 2 s it returns to B. The time period oscillation is (in seconds)
View SolutionThe time taken by a particle performing SHM to pass from point A to B where its velocities are same is 2s. After another 2s it returns to B. The ratio of distance OB to its a amplitude (where O is the mean position) is
View Solution
